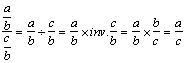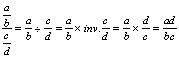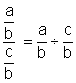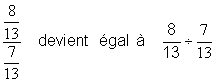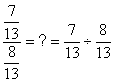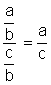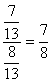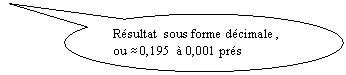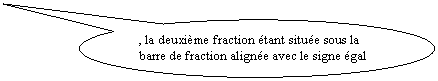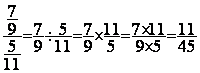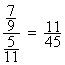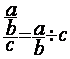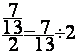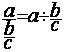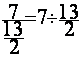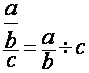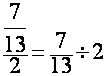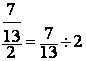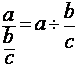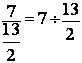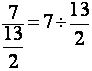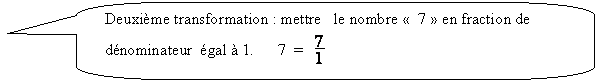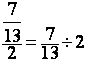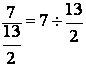|
|
|
|
Définition : La somme de deux fractions est égale à une troisième fraction qui
aura pour
« Numérateur » : la somme des numérateurs et pour
« Dénominateur » : le dénominateur commun.
|
Forme mathématique:
|
« a » et « c » sont les
numérateurs.
|
|
On calcule la somme des numérateurs. « a + c »
|
|
« b » est le dénominateur
|
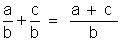
|
|
|
Exemple
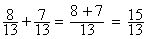
|
|
Le dénominateur commun aux
deux fractions est « b »
|
|
Remarques : ( 15 /13
) cette fraction ne peut plus
« se réduire », elle ne peut plus être simplifiée , on dit que la
fraction est « irréductible ».
Si l’on fait la division de 15/13 on trouve » 1,15384615384615384615384615384615……...
Ce nombre est donné par la calculatrice, la série
de chiffres «1538461 » se répète
à « l’infini » .
|
|
Calculer :
(avec des nombres entiers naturels)
|
|
Calculer :
(avec des nombres entiers relatifs)
|
|
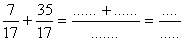
|
|
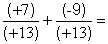 (voir corrigé) (voir corrigé)
|
|
|
|
|
|
i9
|
2. SOUSTRACTION
|
Cd³ INFO 2+
|
|
Règle :
(Forme littérale)
|
|
|
Définition : La différence de deux fractions est égale à une troisième fraction
qui aura pour
« Numérateur » : la différence des numérateurs et pour
« Dénominateur » : le dénominateur commun.
|
|
|
|
|
|
|
|
|
|
|
|
Forme mathématique:
|
« a » et « c » sont les
numérateurs.
|
|
On calcule la différence
des numérateurs. « a - c »
|
|
« b » est le dénominateur
« commun » aux deux fractions.
|
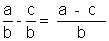
|
|
|
Exemple
Calculer : 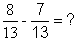
|
|
On conserve le dénominateur
commun aux deux fractions est « b »
|
|
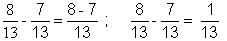 = (1/13) = (1/13)
|
|
|
|
Remarques : ( 1/13
) cette fraction ne peut plus
« se réduire », elle ne peut plus être simplifiée , on dit que la
fraction est « irréductible »)
Si l’on fait la division de 1/13 on trouve » 0,333333333333333333333333333333333……...
Ce nombre est donné par la calculatrice, le nombre
« 3 » se répète à « l’infini » .
Formes
d’expressions du résultat : le résultat peut être exprimé sous forme
d’une fraction irréductible , ou sous forme décimale
« exacte » ou arrondie (
l’arrondi est fixé par celui qui pose l’opération)
Exemple :
l’opération peut s’exprimer
|
|
Forme irréductible
|
Forme décimale (affichage) Forme
décimale arrondi 33ème rang
décimal après la virgule :
|
Forme arrondie :
|
|
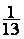
|
0,333333333333333333333333333333333
|
0,33 à 0,01 prés
|
|
Calculs avec des
entiers naturels :
|
|
Calcul avec des entiers relatifs :
|
|
Cas A : le calcul possible :
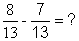 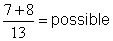 ; parce 8 - 7 est une opération possible avec
des nombres entiers naturels. ; parce 8 - 7 est une opération possible avec
des nombres entiers naturels.
|
|
A) Calculons :
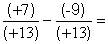
|
|
Cas B : le calcul n’est pas possible (impossible) :
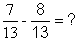 ; ; 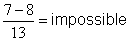
parce « 7 - 8 » est
une opération impossible avec des nombres entiers naturels.
|
|
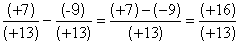
|
|
Remarque : 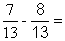 devient possible si
on m’autorise de transformer les
nombres entiers naturels en nombres entiers relatifs : alors j’écris : devient possible si
on m’autorise de transformer les
nombres entiers naturels en nombres entiers relatifs : alors j’écris : 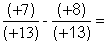
|
|
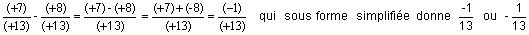
|
|
|
|
|
|
Résultats : 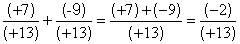
|
|
|
|
|
|
i9
|
3.MULTIPLICATION
|
Cd³ 1 INFO +
Cd³
2 INFO +
|
|
Règle : ( Forme
littérale)
|
|
|
La multiplication de deux
fractions de même dénominateur est
égale à une troisième fraction qui aura pour: « Numérateur » le
produit des numérateurs et pour « Dénominateur » le produit des
dénominateurs.
|
|
Forme symbolique mathématique:
|
|
« a » et « c » sont les
numérateurs
|
|
Le produit des numérateurs est : « ac »
|
|
|
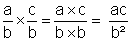
|
|
|
« b » est le dénominateur
« commun » aux deux fractions.
|
|
Le produit des dénominateur est
« b b »
« b² » Le produit d’un nombre par lui - même est
appelé « carré »
|
|
Remarque :
Des opérations avec 2 fractions ;la multiplication de deux fractions est l’opération la plus
simple.
|
|
Exemples :
|
|
Avec des nombres entiers naturels
|
|
Avec des nombres entiers relatifs :
|
|
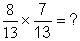
|
|
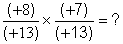 ; ; 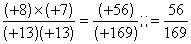
|
|
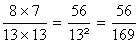
|
|
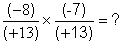 ; ;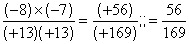
|
|
Calculs : 8 fois 7 = 56 et 13² = 169
Expressions
du résultat :
1°) fraction irréductible : ( 56
/ 169 )
2°) lecture sur écran :
» 0,331360946745562130177514792899
408
3°)Arrondi » 0,331
à 0,001 près .
|
|
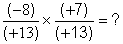 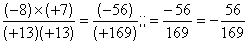
|
|
|
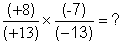 les fractions n’ont pas le même dénominateur ; ( (+13) est différent de (-13) ; voir la deuxième partie de cours sur le
produit de deux fractions de dénominateur différent. les fractions n’ont pas le même dénominateur ; ( (+13) est différent de (-13) ; voir la deuxième partie de cours sur le
produit de deux fractions de dénominateur différent.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i9
|
4
.DIVISION de 2 fractions ( fraction de 2 fractions)
|
Cd³
INFO +
|
|
|
|
|
|
Remarque importante: Nous ne
pouvons pas calculer directement la fraction de deux fractions
,il faut impérativement transformer : La fraction de
fractions doit être transformée en division de deux fractions
|
|
On transforme la fraction de fractions
par une division d’une fraction par l’autre fraction. (en conservant
l’ordre) :à
savoir que :
La fraction en numérateur devient
« dividende » ; la fraction « dénominateur » devient
« diviseur ».
|
|
|
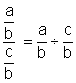
Remarque importante : remarquer que la première
fraction est au dessus de la barre de fraction principale ,
le signe « égal » est aligné
avec ce trait .
la deuxième fraction étant située sous la barre de
fraction alignée avec le signe égal.
|
Application :
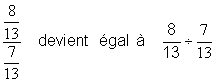
|
|
|
Bien que la fraction de deux fractions soit
transformée en division ;le calcul de la division de deux fractions ne se fait
pas ; il faut
« passer » par la multiplication en respectant la procédure
suivante:
|
|
Procédure
|
Modèle théorique
|
Exemple :
|
|
1°) Première transformation :la fraction de fractions en une division de deux
fractions
|
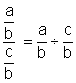
|
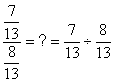
|
|
2°) Deuxième transformation : la division en
multiplication.
Rappel ( Cd ³ )
INVERSE d'un nombre.(ou fraction) :
On se souvient que :
« Diviser un nombre « A » par un
nombre « B »revient à multiplier le premier nombre par l’inverse du
second nombre. »
A : B = A ´ inv. B
« A » est la première fraction et
« B » est la seconde fraction. Il suffit de remplacer : « : B » par «´ inv.
B »
|
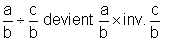
On se souvient que l’
inverse de 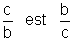
|
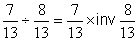
on sait que :
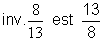
|
|
3ème transformation :.
|

|
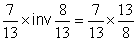
|
|
4ème : on effectue la multiplication On a appliqué ,
les règles de la multiplication de deux fractions :
remarque : « b : b = 1 » et « 13 : 13 = 1 » ce qui
permet de simplifier les facteurs « B » et « 13 »
|
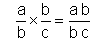 ; on simplifie pou obtenir : ; on simplifie pou obtenir :
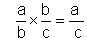
|
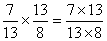
on simplifie :
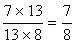
|
|
5°) Conclusion :
|
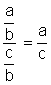
|
Conclusion :
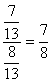 ; = 0,875 ; = 0,875
Dans
le calcul de 7¸ 8 la valeur décimale est exacte
|
|
Règle : (
forme littérale ) Pour
calculer la division de deux fractions il suffit de
multiplier la première fraction par l’inverse de seconde
fraction.
|
|
|
|
|
|
Résultat :
Le résultat de la division de deux
fractions de même dénominateur a pour
numérateur le numérateur de la première fraction et pour dénominateur le
numérateur de la seconde fraction . (voir ci dessus)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+Faire les exercices suivants :
|
Addition
|
|
|
|
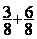 = =
|
|
|
|
Soustraction ( pour cet exercice il faut avoir fait la leçon sur les
nombres relatifs)
|
|
|
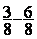
|
|
|
|
Soustraction
|
|
|
|
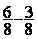 = =
|
|
|
|
Multiplication
|
|
|
|
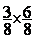
|
|
|
|
Fraction de fractions
|
|
|
|
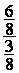 = =
|
|
|
|
Division de fractions
|
|
|
|
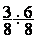
|
|
|
Réponses : 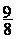 ;
; 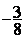 ;
; 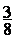 ;
; 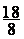 ;
; 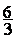 ;
; 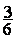
Il faut valider
les acquis précédents avant d’étudier le chapitre « B » (chapitre
suivant)
|
i9
voir ci- dessus.
i29
|
B ) ADDITION ;
SOUSTRACTION ; DIVISION et MULTIPLICATION ;
de DEUX FRACTIONS de
DENOMINATEURS DIFFERENTS.
|
:i
Cd³ INFO +
|
 Soit les deux fractions
Soit les deux fractions  On ne peut pas additionner des
fractions de dénominateurs différents :
On ne peut pas additionner des
fractions de dénominateurs différents :

Ainsi
avant de faire l’addition de deux fractions il faut transformer
chaque fraction en fraction dite « équivalente »
dont le nouveau dénominateur est égal
au produit des deux dénominateurs « bd » .

a) 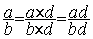
 b)
b) 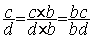
On remplace l’addition 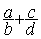 par
par 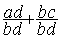

On peut écrire
l’égalité : 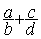 =
= 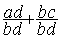
On peut maintenant effectuer l addition des deux fractions:
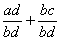 =
=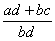
Exemple : Calculer 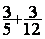
Procédure :
1°) Au préalable on simplifie ou ,dans la mesure du
possible’ on essaie de rendre irréductible
la ou les fractions :
ce qui est le cas de pour 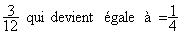
2°) On
remplace l’addition 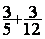 devient égale
à l’addition
devient égale
à l’addition 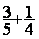
On a remplacé 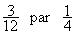 , On obtient
une nouvelle addition ,
, On obtient
une nouvelle addition ,
3°) On calcule le « dénominateur commun » :
5 fois 4 = 20
4°) Transformation
chacune des deux fractions
. (Dont le dénominateur sera
20)

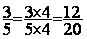 ;
; 
5°) On remplace l’addition avec
les fractions de départ par une nouvelle addition avec des fractions équivalentes :
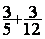 =
= 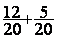
Nous avons maintenant
deux fractions de même dénominateur , nous pouvons
faire l’addition .
6°) Calcul de l’addition :
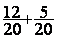 =
= 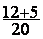 =
= 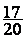
7°) Conclusion :
|
On reprend l’énoncé : l’addition de
départ !
|
On donne le résultat sous
forme irréductible
|
On peut donner aussi le
résultat sous forme décimale
|
|
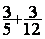
|
= 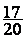
|
= 0,85
|
8°) Vérification : Dans tous les cas il
faut vérifier si notre résultat est
conforme ; pour cela on calcule la
division dans chaque fraction :
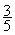 = 3 ¸ 5 = 0,6 ;
= 3 ¸ 5 = 0,6 ; 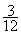 = 3 ¸ 12 = 0,25
= 3 ¸ 12 = 0,25
Ensuite , on
remplace les deux fractions par les valeurs décimales calculées
précédemment et l’on compare :
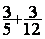 = 0,6 +
0,25 = 0,85
= 0,6 +
0,25 = 0,85
On compare 0,85 avec 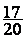 , bien entendu
nous trouvons le même nombre donc on
peut maintenant conclure que :
, bien entendu
nous trouvons le même nombre donc on
peut maintenant conclure que : 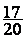 =
= 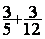
Soit les
deux fractions  On ne peut pas soustraire des fractions de dénominateurs
différents :
On ne peut pas soustraire des fractions de dénominateurs
différents :
Ici le
dénominateur commun sera «
bd »
On doit
transformer les fractions en fractions équivalentes dont on donnera un
dénominateur égal au produit des dénominateurs.
Avant de faire une soustraction il faut :
Transformer chaque
fraction en fraction dite « équivalente »
dont le nouveau dénominateur est
« bd »
.

a) 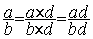
 b)
b) 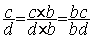
 On
remplace
On
remplace 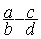 par
par 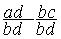
On peut écrire 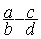 =
= 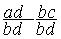
On peut maintenant effectuer la soustraction des deux fractions:
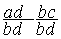 =
=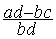
Exemple :
Calculer 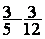
 Procédure :
Procédure :
1°) Rendre irréductible la ou les
fractions : ce qui est le cas de 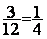
2°) réécrire la nouvelle opération : 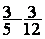 devient égal à
devient égal à 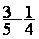
3°)calculer
le dénominateur commun : 5 fois 4
= 20
4°) Transformation les deux
fractions de départ par des fractions équivalentes , ayant toutes deux un même dénominateur .

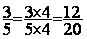 ;
; 
5°) Remplacer les fractions de la
soustraction d’origine par les fractions équivalentes :
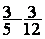 =
= 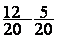
Nous sommes en présence de deux
fractions de même dénominateur
6°) calcul de la soustraction :
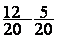 =
= 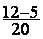 =
= 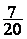
Résultat sous forme irréductible
7°) 1ère conclusion :
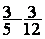 =
= 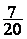 =
0,35
=
0,35
0,35 représente le résultat sous
forme décimale
8°) Vérification : 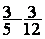 = 0,6 -
0,25 = 0,35 ; et
= 0,6 -
0,25 = 0,35 ; et 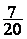 =
0,35 ; conclusion
=
0,35 ; conclusion
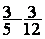 =
= 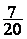
|
Si l’addition et la soustraction de deux
fractions de dénominateurs
différents posent un réel
problème , il n’en est pas de même
pour la multiplication et la division ( ou fraction ) de
fractions : il n’y a aucune transformation particulière , il faut
appliquer directement les
règles énoncées pour les fractions de même dénominateur .
|
Voir suite du cours .
Il n’y a
pas de transformation particulière
à effectuer , ainsi la multiplication de deux fractions de dénominateur
différent ne pose pas de problème
particulier .
On retiendra la règle suivante :
|
Règle : ( écriture
littérale)La
multiplication de deux fractions de dénominateur différent est égale à une
troisième fraction qui aura pour
« Numérateur » : le produit des numérateurs et pour
« Dénominateur » : le produit des dénominateurs.
|
Traduction
symbolique mathématique: 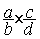 =
= 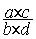 =
= 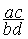
 Exemple : calculer :
Exemple : calculer : 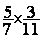
Solution :

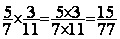

conclusion : 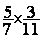 =
= 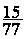 » 0,194805194805194805194805194805195
» 0,194805194805194805194805194805195
 iNous ne pouvons pas calculer directement la fraction de
deux fractions ,il faut impérativement transformer
l’écriture .
iNous ne pouvons pas calculer directement la fraction de
deux fractions ,il faut impérativement transformer
l’écriture .
 Donc
l’écriture :
Donc
l’écriture : 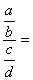 se
transforme en
se
transforme en 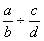
 La fraction de fractions
La fraction de fractions 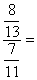 devient
devient 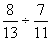
 Bien que
la fraction de fractions soit transformée en division ; la division de deux
fractions ne se fait pas ; il faut transformer la division en multiplication en respectant
la procédure suivante:
Bien que
la fraction de fractions soit transformée en division ; la division de deux
fractions ne se fait pas ; il faut transformer la division en multiplication en respectant
la procédure suivante:
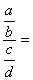 se
transforme en
se
transforme en 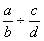 qui
devient
qui
devient 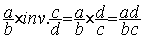
En conclusion : 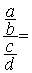
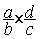

Rappel ( Cd ³
) INVERSE d'un nombre.(ou fraction) :l’
inverse de 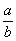 est égal à
est égal à 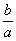 et inv.
et inv. 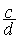 =
= 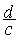
Et l’on applique ,ensuite, les règles de la multiplication de deux
fractions.
|
Règle : ( forme littérale ) Pour
calculer la division de deux fractions il suffit de
multiplier la première fraction par l’inverse de seconde
fraction.
|
Forme symbolique
mathématique :
Exemple : 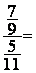
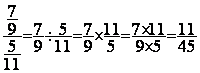 ( »0,244444444444444444444444444444444)
( »0,244444444444444444444444444444444)
Conclusion : 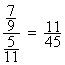 ;
»0,24 à 0,01 près
( il faudrait faire
la vérification ! !)
;
»0,24 à 0,01 près
( il faudrait faire
la vérification ! !)
+Faire les exercices suivants
|
Addition
|
|
|
|
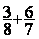 = =
|
|
|
|
Soustraction ( pour cet exercice il faut avoir fait la leçon sur les
nombres relatifs
|
|
|
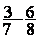 = =
|
|
|
|
Soustraction
|
|
|
|
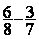 = =
|
|
|
|
Multiplication
|
|
|
|
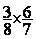 = =
|
|
|
|
Fraction de fractions
|
|
|
|
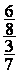 = =
|
|
|
|
Division de fractions
|
|
|
|
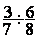 = =
|
|
|
iComme vous
l’avez remarqué :
on peut multiplier ou
diviser directement deux fractions de
dénominateur différent , on ne peut pas additionner ou
soustraire deux fractions qui
n’ont pas le même dénominateur .
Addition d’une fraction avec un nombre entier
(naturel ou relatif)
Modèle mathématique: 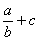 = ?
= ?
 Exemple:
Exemple: 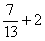 = ?
= ?
idans
l’addition , Que le nombre soit devant
ou derrière la fraction le résultat ne changera pas : 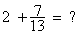 ( cela ne
sera pas vrai avec la soustraction )
( cela ne
sera pas vrai avec la soustraction )
Procédure pour transformer l ‘ addition
( ou la soustraction ) en addition ( ou soustraction) de deux
fractions de même dénominateur.
1°)Rendre la
fraction
irréductible.:
Exemple : 7 /13
= 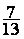
2°)Mettre le nombre
sous forme de fraction de dénominateur égal à
1
Modèle mathématique: c =  ;
Exemple : 2 =
;
Exemple : 2 = 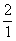
3°)Transformer cette fraction en fraction
équivalente de dénominateur égal au dénominateur de la première
fraction.
Modèle mathématique: 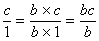
Le dénominateur de la première fraction est 13
donc 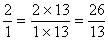 =
=
4°) Poser la nouvelle égalité
Modèle mathématique: 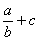 =
= 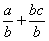
donc 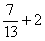 =
= 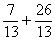
5°) Faire l’addition des deux fractions de même dénominateur. 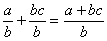
donc 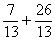 =
= 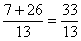
6° ) il faudra conclure (comme on l’a vu pour les
exercices précédents ), après
vérification.
Soustraction d’une fraction avec un nombre entier
(naturel ou relatif)
 Modèle mathématique:
Modèle mathématique: 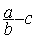 = ?
= ?
 Exemple:
Exemple: 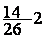 = ?
= ?
iContrairement
à l’addition , pour la soustraction , si l’on permute
le nombre et la fraction on n’aura pas
le même résultat:
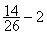 ¹
¹ 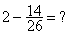
Procédure pour transformer la
soustraction d’un nombre et d’une
fraction en soustraction de deux fractions de même dénominateur.
( nous ne
traiterons que l’exemple de
soustraction : 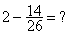 )
)
procédure :
1°)Rendre
la fraction
irréductible.:
Exemple : la fraction irréductible de 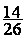 est
est 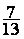
2°)Mettre le nombre
sous forme de fraction de dénominateur égal à 1
Modèle mathématique: c =  ; exemple : 2
=
; exemple : 2
= 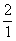
3°)Transformer cette fraction en fraction
équivalente de dénominateur égal au
dénominateur de la première fraction.
Modèle mathématique: 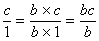
Le dénominateur de la première fraction est 13
donc 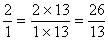
4°) poser la nouvelle égalité
Modèle mathématique: 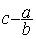 =
= 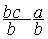
donc 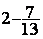 =
= 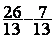
5°) faire la soustraction des deux fractions de même
dénominateur.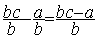
donc 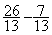 =
= 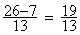
6° ) il faudra conclure (comme on l’a vu pour les
exercices précédents ), après
vérification.
|
Par définition : On ne
peut pas multiplier un nombre par une fraction ,
pour obtenir un résultat on prendra appui sur la règle concernant la multiplication
de deux fractions .
|

Modèle mathématique: 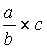 =
=
Exemple : 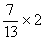 = ? ;
= ? ;
On passe de ce
modèle mathématique: 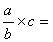 à ce modèle
à ce modèle 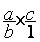
Remarque : Il faut mettre le nombre
« c » sous forme de fraction de dénominateur égal à 1
; tel que c =
 3° ) On applique la procédure concernant la multiplication de
deux fractions:
3° ) On applique la procédure concernant la multiplication de
deux fractions:
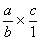 =
=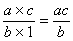
4° )
Rendre compte: 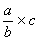 =
=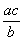
Exemple : 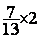 =
=
Solution : 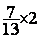 =
= 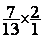 =
= 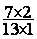 =
= 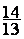
 Conclusion :
Conclusion :
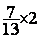 =
= 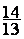
Cas particulier 1 : on veut calculer : 3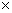
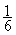 = ;
= ; 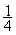
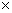 72
72
Modèle mathématique: 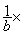 a = pas
de solution immédiate ; (il faut
transformer)
a = pas
de solution immédiate ; (il faut
transformer)
Exemple : si
b = 2
Exemple 1 : Calculer 3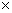
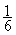 = ? ( donner le résultat sous forme d’une fraction simplifiée ; puis
sous la forme décimale )
= ? ( donner le résultat sous forme d’une fraction simplifiée ; puis
sous la forme décimale )
3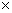
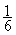 =
= 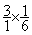 ( voir multiplication de deux fractions)
( voir multiplication de deux fractions)
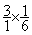 =
= 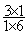 ;
; 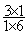 =
=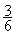 (voir
simplification d’une fraction)
(voir
simplification d’une fraction)
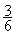 =
= 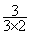 ;
; 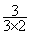 =
= 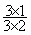 ;
; 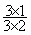 =
= 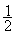
conclusion : 3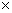
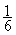 =
= 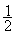 ; remarque :
(
; remarque :
(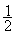 = 0,5 ),
sous forme décimale 3
= 0,5 ),
sous forme décimale 3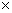
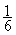 = 0,5
= 0,5
Exemple 2 : calculer

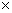 72 ( donner le
résultat sous forme d’une fraction
simplifiée ; puis sous la forme décimale )
72 ( donner le
résultat sous forme d’une fraction
simplifiée ; puis sous la forme décimale )

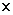 72 =
72 = 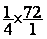 =
=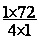 ;
; 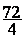 =
= 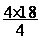 ;
; 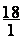
Conclusion : 
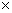 72 =
72 =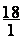 ou
ou 
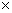 72 = 18
72 = 18
En
résumé : On ne peut pas multiplier un
nombre par une fraction , pour obtenir un résultat on
prendra appui sur la règle concernant la multiplication de deux fractions.
Procédure permettant de multiplier
une fraction par un nombre.( Modèle mathématique: 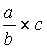 = ) Il faut faire dans l’ordre :
= ) Il faut faire dans l’ordre :
a) Placer le nombre sous forme de
fraction de dénominateur égal à 1 : 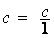
b) On passe de ce modèle
mathématique: 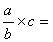 à ce modèle
à ce modèle 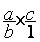
c) On applique la procédure
concernant la multiplication de deux fractions:
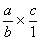 =
=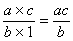
d ) Rendre
compte: 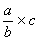 =
=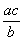
Attention: on ne doit pas confondre:
« diviser une fraction par un nombre(
entier) » ( 1° cas):
ET
« diviser un nombre ( entier) par une
fraction »(2° cas)
iCe qui
différencie les deux cas est la position du signe « égal »
devant l ‘ une des deux barres de
fraction :
Etude
du 1° cas : « diviser une fraction par un nombre(
entier) »
 1°) Première transformation
1°) Première transformation
Exemple: 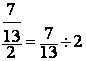
2°) Deuxième transformation
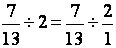
 3°) Troisième
transformation : seconde. »
3°) Troisième
transformation : seconde. »
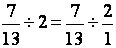 =
= 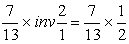
4°) Calcul : appliquer la règle concernant la
multiplication de deux fractions.

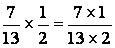 =
= 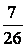
Etude du second cas : Division d’un nombre "a" entier
par une fraction

 Exemple :
Exemple : 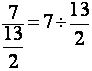
1°) Transformer la division d’un nombre par une
fraction en une division de fraction par
une fraction.
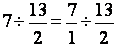
2°) Multiplier la première fraction par l ‘inverse de
la seconde. »
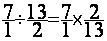
4°) Faire la
multiplication des deux fractions.

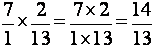
ion peut constater
que les deux cas donnent des résultats différents ,il est donc trés important de vérifier la position du signe
« égal »
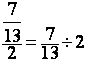 donne
comme résultat:
donne
comme résultat: 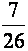 » 0,……
» 0,……
et 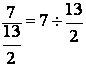 donne comme
résultat:
donne comme
résultat: 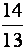 » 1,……
» 1,……
+Faire les exercices suivants
|
Addition
|
|
|
|
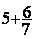 = =
|
|
|
|
Soustraction ( pour cet exercice il faut avoir fait la leçon sur les
nombres relatifs)
|
|
|
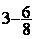 = =
|
|
|
|
Soustraction
|
|
|
|
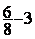 = =
|
|
|
|
Multiplication
|
|
|
|
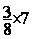 = =
|
|
|
|
Fraction de fractions
|
|
|
|
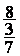 = =
|
|
|
|
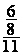 = =
|
|
|
|
Division de fractions
|
|
|
|
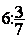 = =
|
|
|
|
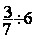 = =
|
|
|
Cd³ INFO
+
( Voir la partie
abordée dans la leçon N°2 sur la fraction)
 A
savoir : a% =
A
savoir : a% = 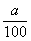

y = 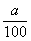 x ;
ou y =
x ;
ou y = 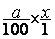 =
= 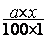 =
= 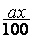
ou
« y » est la valeur
d’une augmentation ou diminution
« a » la
valeur du taux
« x » le nombre sur lequel
s’applique le taux.
Exemple : on veut
calculer 8 % de 120
On transforme :
8% = 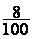 ( = 0,08 )
( = 0,08 )
On calcule : 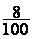 ´ 120 =
´ 120 = 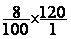 =
= 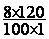 =
= 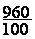 = 9,6
= 9,6
Conclusion :
8% de 120 = 9,6
|
Leçon
|
Titre
|
|
N°5
|
TRAVAUX d ’ AUTO - FORMATION
sur
LES FRACTIONS ( OPERATIONS
)
|
TRAVAUX N°5
d ’ AUTO - FORMATION : CONTROLE
1°) donner la définition
d’un fraction : donner un exemple avec 3 et 4
.
Exemples ?:
2°) Qu’est ce qu’un
rationnel ?
.
Donner des exemples :
16 : 2 = ? ………………………………………………
25: 4 =
? ………………………………………………
11 : 7 =
? …………………………………………………
3°) qu’appelle - t - on
« écriture fractionnaire »
|
A. ADDITION ; SOUSTRACTION ;
MULTIPLICATION ; DIVISION de DEUX
FRACTIONS DE MEME DENOMINATEUR .
|
Cd³ INFO +
|
1°) A quoi est égale la somme de deux fractions ? ( Forme littérale)
2°) Donner la Forme symbolique mathématique:
1°) A quoi est égale la différence de deux fractions de même
dénominateur ? ( Forme
littérale)
2°) donner la Forme symbolique mathématique:
1°) A quoi est égale la différence de deux fractions de même
dénominateur ? ( Forme littérale)
.
2°) donner sa forme symbolique mathématique:
1°) Compléter la phrase :
Remarque
importante: Nous ……………………. calculer
directement la fraction de deux fractions ,il faut impérativement transformer
2°) Transformer la fraction de fractions en division de
fractions :
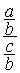 se transforme en
se transforme en
3°) A quoi est
égale le résultat de la division de deux
fractions de même dénominateur ? ( Forme littérale)
5° ) montrer les étapes de transformation conduisant au
résultat .
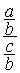 =
= 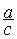
|
B ) ADDITION ; SOUSTRACTION ;
MULTIPLICATION ; DIVISION de DEUX
FRACTIONS DE DENOMINATEURS DIFFERENTS.
|
Cd³ INFO +
|
1°) Soit les deux fractions 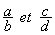 que peut - on déclarer sur l’addition de ces deux
fractions ?
que peut - on déclarer sur l’addition de ces deux
fractions ?
2°)Ainsi avant de faire l’addition de deux fractions de
dénominateurs différents il faut
transformer chaque fraction en fraction dites « ………………. » dont le
nouveau dénominateur est «
bd » ( appelé :…………………………………..) .
3°) transformer 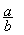 en fraction équivalente de dénominateur valant
« bd »
en fraction équivalente de dénominateur valant
« bd »
4°) transformer 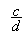 en fraction
équivalente de dénominateur valant « bd »
en fraction
équivalente de dénominateur valant « bd »
5 ° )
faire l’addition des fractions :
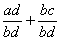 =
=
1°) Soit les deux fractions 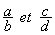 que peut - on déclarer sur la soustraction de ces deux fractions ?:
que peut - on déclarer sur la soustraction de ces deux fractions ?:
2°)Ainsi avant de faire l’addition
de deux fractions de dénominateurs différents
il faut transformer chaque
fraction en fraction dites
« ……………. » dont le nouveau
dénominateur est « bd »
(appelé : ………………………………) .
3°) transformer 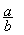 en fraction équivalente de dénominateur valant
« bd »
en fraction équivalente de dénominateur valant
« bd »
4°) transformer 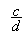 en fraction
équivalente de dénominateur valant « bd »
en fraction
équivalente de dénominateur valant « bd »
5 ° )
faire la soustraction des fractions :
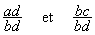
1°) à quoi est égale la multiplication de deux fractions
de dénominateurs différents ? ( écriture
littérale) ?
2°) donner la traduction
symbolique mathématique: 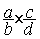 =
=
1°) Compléter la phrase :
Remarque
importante: Comme pour la division de deux fractions de même
dénominateur , nous ……………………. calculer
directement la fraction de deux fractions de dénominateur différent , il faut impérativement transformer
2°) Transformer la fraction de fractions en division de
fractions :
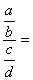 se transforme en
se transforme en
4°) A quoi est
égale le résultat de la division de deux
fractions de même dénominateur ? ( Forme littérale)
5° ) montrer les étapes de transformation conduisant au
résultat .
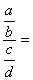
3°) Donner la forme symbolique mathématique du
calcul de 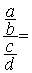 ?
?
|
C) ADDITION ;
SOUSTRACTION ; MULTIPLICATION ; DIVISION d’ UNE
FRACTION et d’UN NOMBRE .
|
Cd³ INFO +
|
1° ) On
ne peut pas additionner ( 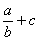 = ?….) une fraction avec un nombre
entier (naturel ou relatif) que faut-il faire pour obtenir un résultat ?
= ?….) une fraction avec un nombre
entier (naturel ou relatif) que faut-il faire pour obtenir un résultat ?
2° ) Modèle mathématique: 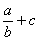 = ?
= ?
3°) donner la procédure à
appliquer pour transformer l ‘ addition
( ou la soustraction ) d’une fraction et un
nombre en addition ( ou soustraction) de
deux fractions de même dénominateur en vue faire cette addition ou
soustraction ?.
1° ) On ne
peut pas additionner (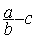 = ?.) une fraction avec un nombre entier (naturel ou relatif) que
faut-il faire pour obtenir un résultat ?
= ?.) une fraction avec un nombre entier (naturel ou relatif) que
faut-il faire pour obtenir un résultat ?
2°) donner la procédure à
appliquer pour transformer la soustraction
d’une fraction et un nombre en
soustraction de deux fractions de même dénominateur en vue faire cette
soustraction ?.
1°) peut - on multiplier un nombre
par une fraction ?
2°) donner la procédure permettant
de multiplier une fraction par un nombre.
Etude du 1° cas : « diviser une fraction par
un nombre( entier) »
1°) Donner la procédure permettant de calculer le résultat
de la division d’une fraction par un nombre : 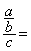
2°)Etude
du second cas :
Division d’un nombre "a"
entier par une fraction
Donner la procédure permettant
de calculer le résultat de la division d’un nombre par une fraction: 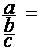
1°) avec 3 et 4
écrire une fraction ?
2°) souligner
les rationnels .
16 + 2 = 18
; 16 : 2 = 8 ; 16 -2 = 14
25: 4 =
6,25 ; 25 ´ 4 = 100 ; 25 - 4 =
21
11 + 7 =
18 ; 7 - 11 = -4 ; 11 : 7 =
11/7
3°) entourer l ’
« écriture fractionnaire »
16 /
2 ; 17 / 5 ;
20,2 / 2 ; 10 / 0,5 ;
6,3 / 7,8 ; .456/ 3625
|
A. ADDITION ; SOUSTRACTION ;
MULTIPLICATION ; DIVISION de
DEUX FRACTIONS DE MEME DENOMINATEUR .
|
Cd³ INFO +
|
A)
Série 1
|
1. ADDITION de DEUX FRACTIONS DE
MEME DENOMINATEUR .
|
Cd³ INFO 1 +
|
Calculer :
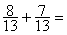
|
2.SOUSTRACTION de DEUX
FRACTIONS DE MEME DENOMINATEUR .
|
Cd³
INFO 2+
|
Calculer : 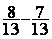 ; donner le
résultat sous forme irréductible et sous
forme décimale à 0,01 prés .
; donner le
résultat sous forme irréductible et sous
forme décimale à 0,01 prés .
|
3.MULTIPLICATION de DEUX
FRACTIONS DE MEME DENOMINATEUR .
|
Cd³
INFO +
|
Calculer 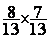 donner le
résultat sous forme irréductible et sous
forme décimale à 0,001 prés .
donner le
résultat sous forme irréductible et sous
forme décimale à 0,001 prés .
|
4 .DIVISION
de DEUX FRACTIONS DE
MEME DENOMINATEUR .
|
Cd³
INFO +
|
1°) transformer 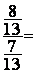 en une division de
deux fractions :
en une division de
deux fractions :
2°) Calculer : 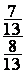 = ; donner le
résultat sous forme irréductible et sous
forme décimale à 0,001 prés .
= ; donner le
résultat sous forme irréductible et sous
forme décimale à 0,001 prés .
A) Série 2
|
Série 2 : Faire les calculs de DEUX FRACTIONS DE
MEME DENOMINATEUR
|
|
.
|
Addition
|
|
|
|
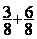 = =
|
|
|
|
Soustraction ( pour cet exercice il faut avoir fait la leçon sur les
nombres relatifs)
|
|
|
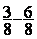
|
|
|
|
Soustraction
|
|
|
|
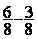 = =
|
|
|
|
Multiplication
|
|
|
|
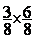
|
|
|
|
Fraction de fractions
|
|
|
|
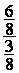 = =
|
|
|
|
Division de fractions
|
|
|
|
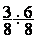
|
|
|
|
B ) ADDITION ; SOUSTRACTION ;
MULTIPLICATION ; DIVISION de DEUX
FRACTIONS DE DENOMINATEURS DIFFERENTS.
|
Cd³ INFO +
|
B) Série 1
Calculer : 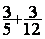 ; donner le
résultat sous forme irréductible et sous
forme décimale à 0,001 prés .
; donner le
résultat sous forme irréductible et sous
forme décimale à 0,001 prés .
Calculer 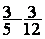 ; donner le résultat sous
forme irréductible et sous forme
décimale à 0,001 prés .
; donner le résultat sous
forme irréductible et sous forme
décimale à 0,001 prés .
1°) Calculer : 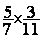 ; donner le résultat sous forme
irréductible et puis sous forme décimale à 0,001 prés .
; donner le résultat sous forme
irréductible et puis sous forme décimale à 0,001 prés .
Calculer 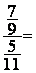 ? ;
donner le résultat sous forme irréductible et puis sous forme décimale à
0,001 prés .
? ;
donner le résultat sous forme irréductible et puis sous forme décimale à
0,001 prés .
|
Addition
|
|
|
|
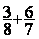 = =
|
|
|
|
Soustraction ( pour cet exercice il faut avoir fait la leçon sur les
nombres relatifs
|
|
|
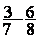 = =
|
|
|
|
Soustraction
|
|
|
|
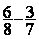 = =
|
|
|
|
Multiplication
|
|
|
|
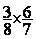 = =
|
|
|
|
Fraction de fractions
|
|
|
|
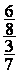 = =
|
|
|
|
Division de fractions
|
|
|
|
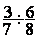 = =
|
|
|
|
C) ADDITION ;
SOUSTRACTION ; MULTIPLICATION ; DIVISION d’ UNE
FRACTION et d’UN NOMBRE .
|
Cd³ INFO +
|
C ) Série 1
1°) Calculer : 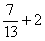 = ? ou
= ? ou 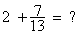
1°) Calculer : 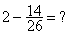 ;
donner le résultat sous forme d’une
fraction simplifiée ; puis sous la forme décimale à 0,01 prés .
;
donner le résultat sous forme d’une
fraction simplifiée ; puis sous la forme décimale à 0,01 prés .
2°) 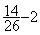 = ? ; donner le
résultat sous forme d’une fraction
simplifiée ; puis sous la forme décimale à 0,01 prés .
= ? ; donner le
résultat sous forme d’une fraction
simplifiée ; puis sous la forme décimale à 0,01 prés .
1°) Calculer : 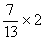 =
? donner
le résultat sous forme d’une fraction
simplifiée ; puis sous la forme décimale à 0,01 prés .
=
? donner
le résultat sous forme d’une fraction
simplifiée ; puis sous la forme décimale à 0,01 prés .
2 °) calculer 3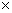
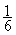 = ; donner le résultat sous forme d’une fraction simplifiée ; puis
sous la forme décimale à 0,01 prés .
= ; donner le résultat sous forme d’une fraction simplifiée ; puis
sous la forme décimale à 0,01 prés .
3°)
calculer 
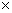 72 donner le résultat sous forme d’une fraction simplifiée ; puis
sous la forme décimale à 0,01 prés .
72 donner le résultat sous forme d’une fraction simplifiée ; puis
sous la forme décimale à 0,01 prés .
Etude du 1° cas : « diviser une fraction par
un nombre( entier) »
1°) calculer : 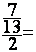 ; donner le résultat sous forme d’une fraction simplifiée ; puis
sous la forme décimale à 0,001 prés .
; donner le résultat sous forme d’une fraction simplifiée ; puis
sous la forme décimale à 0,001 prés .
2°)Calculer : 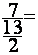 ; donner le résultat sous forme d’une fraction simplifiée ; puis
sous la forme décimale à 0,001 prés .
; donner le résultat sous forme d’une fraction simplifiée ; puis
sous la forme décimale à 0,001 prés .
|
Addition
|
|
|
|
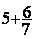 = =
|
|
|
|
Soustraction ( pour cet exercice il faut avoir fait la leçon sur les nombres
relatifs)
|
|
|
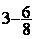 = =
|
|
|
|
Soustraction
|
|
|
|
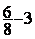 = =
|
|
|
|
Multiplication
|
|
|
|
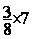 = =
|
|
|
|
Fraction de fractions
|
|
|
|
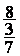 = =
|
|
|
|
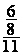 = =
|
|
|
|
Division de fractions
|
|
|
|
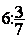 = =
|
|
|
|
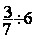 = =
|
|
|
|
4 . Cas
particulier : pourcentage d’un nombre .
|
Cd³
INFO +
|
1°) Calculer 8 % de
120
PROBLEMES :FRACTIONS ( Série1)
FRACTION D'UNE
GRANDEUR
|
Les problèmes sont à faire :
(dans un premier temps
faire le calcul et donner le résultat) ; dans un deuxième temps, lors d’un
devoir , vous devrez rédiger ;
|
|
1) Une salle de cinéma qui
compte 320 places est remplie aux ¾. Combien y a-t-il de places occupées ?
Combien reste-t-il de places libres ?
2) La France a une superficie de
549 000 km² dont ¼ est recouvert de forêts. Quelle est la superficie de la
forêt française ?
3) Une famille répartit ses
revenus en prévoyant notamment : 2/20 pour les impôts, 5/20 pour l'alimentation
et 3/20 pour le loyer. Les revenus mensuels de la famille étant de 15 50 €,
calculer en euros, le montant des dépenses prévues pour les impôts,
l'alimentation et le loyer.
4) Les 4/10 des 330 000 habitants de la Martinique
ont moins de 20 ans. Trouver la question et y répondre.
5) Une personne qui a gagné
107 80 € au Loto offre 1/7 de son gain à
l'association "Médecins du Monde" et 3/7 à une association pour la
recherche contre le cancer. Quelle somme a-t-elle offerte à chacune de ces
associations ? Combien a-t-elle gardé ?
6) Sur un terrain
constructible de 1 395 m², 1/9 est
réservé à la maison et 2/5 au jardin potager. Le reste de la surface sera
ensemencé en pelouse. Quelle sera la superficie occupée par cette pelouse ?
7) Le vélo de cross d'Alain
vaut 720 €. Celui de Stéphane coûte les 9/6 de celui
d'Alain. Quel est le prix du vélo de Stéphane ?
8) Maman a 33 ans. L'âge de
Papa est égal aux 7/6 de celui de Maman. Quel est
l'âge de Papa ?
9) Des maçons doivent
construire un mur de 25 m de long. La première journée, ils en édifient les
2/5, puis ¼ le lendemain. Quelle longueur de mur leur restera-t-il à construire
le troisième jour ?
10) Romain prépare un cocktail
pour ses camarades. Dans un saladier d'une capacité de 3,5 l, il doit verser
3/10 de jus d'ananas, 1/5 de jus d'orange, 1/14 de sirop de grenadine et
compléter avec de l'eau gazeuse. Quelle quantité (en litres) de chaque
ingrédient doit-il utiliser ?
11) Pour arroser son jardin,
papa récupère l'eau de pluie dans une citerne, d'une capacité de 2 700 l. Celle-ci est actuellement remplie au
4/5. Sachant qu'il utilise environ 90 l d'eau par jour, en aura-t-il
suffisamment pour une durée de trois semaines sans pluie ?
12) Un jardinier dispose d'une
citerne d'une capacité de 2 500 l. Il en tire d'abord 1/5, puis les 3/5 de ce qu'il reste. Quelle quantité d'eau, en litres,
a-t-il utilisée chaque fois ? Quelle quantité d'eau reste-t-il dans la citerne
?
13) Monsieur Léman achète un
canapé valant 23 75 €. Il paie 1/8 de cette somme à la commande, 3/8 à la
livraison et le reste en 4 mensualités égales. Combien verse-t-il à la commande
? A la livraison ? Combien versera-t-il à chaque mensualité ?
14) Un train peut transporter
420 voyageurs, mais il n'est plein qu'au 5/7. Un quart des passagers voyage en
première classe. Combien de personnes voyagent en seconde classe ?
15) Pour un match de football
international, les 7/8 des 50 000 places du Parc des
Princes sont occupées. 4/5 des spectateurs ont payé leur place, les autres
bénéficient d'invitations. Quel est le nombre de spectateurs assistant
gratuitement au match ?
16) Le grand frère de Mathieu
achète une moto valant 8 880 €. Il verse d'abord 1/3 de cette somme à la
commande, puis, à la livraison, les ¾ de ce qu'il devait encore. Ses parents
paient le reste. A combien s'élève la participation de ses parents ?
17) L'Europe compte environ 800
millions d'habitants, soit à peu près le 1/6 des hommes vivant sur la Terre,
mais elle n'occupe que le 1/16 des continents qui couvrent 136 millions de km².
Quelle est, environ, la population de la Terre ? Quelle est la superficie de
l'Europe ?
GRANDEUR D'APRÈS
UNE FRACTION
1) Un concurrent à moto du
rallye Paris -Dakar tombe et abandonne aux 6/7 de la
compétition après 18 jours de course. Quelle est, en jours, la durée totale de
l'épreuve ?
2) Patrick revend son
skate-board ; avec les 2/3 de ce qu'il a ainsi gagné,
il s'achète un disque valant 6,5 €. Combien avait -il
revendu son skate-board ?
3) On achète une voiture
d'occasion coûtant les 5/8 du prix du même modèle, à
l'état neuf. Si l'on a payé cette voiture 13 200 €, combien valait-elle neuve ?
4) Dans un appartement, la
salle de bains occupe les 2/35 de la superficie habitable, soit 6,5 m².
Calculer la superficie habitable de cet appartement.
5) Une bouteille est remplie aux 2/3. Il faudrait y ajouter encore 25 cl pour la remplir
complètement. Quelle est la capacité de cette bouteille ?
6) A la Bourse, un homme
d'affaires perd les 4/7, soit 280 00 €, de son capital. Quel était le capital
initial ? Calculer le montant de la perte si elle avait correspondu aux 3/5 du capital.
7) Ingrid partage avec ses 3
frères et sœurs les 5/7 de son gain au Loto et , avec
le reste, achète une plante verte pour sa mère. Chacun des enfants reçoit 35 €.
Combien Ingrid avait-elle gagné ? Quel est le prix de la plante verte ?