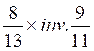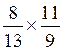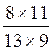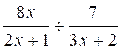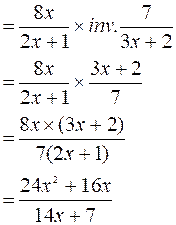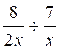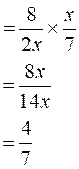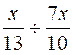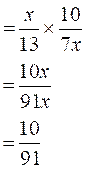|
|
|
Expression d' un résultat
|
|
|
Fraction irréductible |
|
|
Arrondir "à tant prés" ;troncature |
ENVIRONNEMENT du dossier :
|
|
Liste de teste et renvoi à des cours sur les
opérations avec « les fractions « |
|
DOSSIER : DIVISON de deux fractions de dénominateurs différents.
|
TEST |
COURS |
|
Définition: Division de
deux fractions ayant des dénominateurs différents :exemple 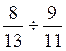
Modèle mathématique: 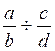 = ne se fait pas,
voir transformation dans « cas général »
= ne se fait pas,
voir transformation dans « cas général »
Il
faut multiplier la première par l 'inverse de la seconde voir Objectif division niveau..1
|
Exercice type |
|
Résultat : |
|
|
|
|
Voici
trois cas :la soustraction s'opère de la même façon
qu'avec un nombre de dénominateur commun
|
a)
Sans autre difficulté |
|
|
|
|
|
b ) idem |
|
|
|
|
|
c )idem |
|
|
|
|
On dit que ![]()
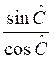 et que
et que 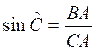 ;
; 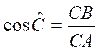 ;
;
exprimer ![]() en fonction des longueurs .
en fonction des longueurs .
TRAVAUX AUTO FORMATIFS.
1°) Comment procède -
t- on pour effectuer la Division de deux fractions ayant des dénominateurs
différents ?
1°) Faire les divisions suivantes :
a) 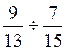 = b )
= b ) 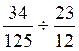 = c )
= c ) 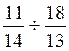 = ;
= ;
2° ) idem
a ) 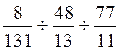 =
=
A
partir de cet exercice ,on peut s’interroger sur les
valeurs que l’on doit exclure au dénominateur, parce que l’on ne peut diviser
par 0 )
b ) 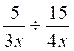 =
=
3°) Idem
a) 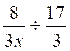 = b)
= b) 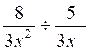 =
=
Trigonométrie
4° ) montrer que : :![]() =
= ![]() ;
; 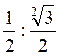 =
= 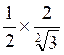 =
= ![]() on transforme
on transforme ![]() en multipliant le
« haut » et le « bas » par
en multipliant le
« haut » et le « bas » par ![]() ; pour
« neutraliser » le
; pour
« neutraliser » le ![]() du dénominateur.
du dénominateur.