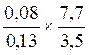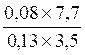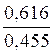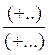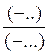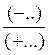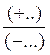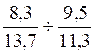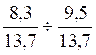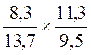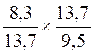division de deux en écritures fractionnnaires

Pré requis : Objectif : QIII div.5

Eventuellement voir : Mettre une écriture fractionnaire sous forme de fraction
Inverse d 'une fraction ou d'un nombre "en niveau +"
Fraction (nomenclature)
Multiplication de deux fractions de même dénominateur

Expression d' un résultat
Fraction irréductible
Arrondir "à tant prés" ;troncature

ENVIRONNEMENT du dossier :

Index

Objectif précédent

Objectif suivant

Tableau 162

DOSSIER :Division de deux écritures fractionnaires: 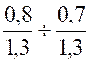ou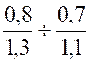

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

LA FRACTION DE FRACTIONS NE SE FAIT PAS ? ON LA TRANSFORME EN DIVISION , Mais LA DIVISION NE SE FAIT PAS ,IL FAUT LA TRANSFORMER EN MULTIPLICATION

Division de deux écritures fractionnaires.

Exemple :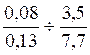

Procédure: Transformer la division en multiplication: multiplier la première écriture fractionnaire par l'inverse de la seconde écriture fractionnaire.

Voir l’ objectif :

Multiplication de deux écritures fractionnaires

Exemple type
	= = =

Rappel : division entre deux nombres relatifs
Traduction des règles en modèles mathématiques de la division d’un nombre relatif par un autre nombre relatif : * val : lire valeur absolue *Val₃ est un « rationnel »
Même signe : ( + val ₁ ) : ( + val₂) = ( + (val₁ : val₂) ) = + val₃ ( - val ₁ ) : ( - val₂) = ( + (val₁ : val₂) ) = + val₃	Sous forme fractionnaire : = (+……) = (+……)
Signe contraire : ( - val ₁ ) : ( + val₂) = (- (val₁ : val₂) ) = - val₃ ( + val ₁ ) : ( - val₂) = ( - (val₁ : val₂) ) = - val₃	Sous forme fractionnaire : = (-……) = (-……)

CAS : division de deux écritures fractionnaires possédant des numérateurs et dénominateurs « relatifs »

Le quotient	Devient l’opération suivante
: =	(+..) : (+….) =
: =	(+..) : (+….) =
: =	(+..) : (+….) =
: =	(-….) :(+….) =
:=	(-….) : (+….) =
:=	(-….) : (+….) =
:=	(-….) : (+….) =

INTERDISCIPLINARITE

TRAVAUX AUTO FORMATIFS.

CONTROLE:

Donner la transformation de la division de deux écritures fractionnaires.

EVALUATION:

Exercices	Résultats

CORRIGE

CONTROLE:

Donner la transformation de la division de deux écritures fractionnaires.

Transformer la division en multiplication: il faut multiplier la première écriture fractionnaire par l'inverse de la seconde écriture fractionnaire

EVALUATION:

Exercices	Résultats

	= =