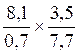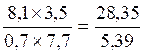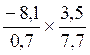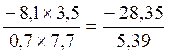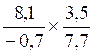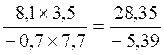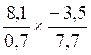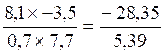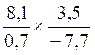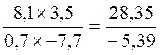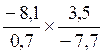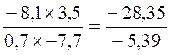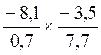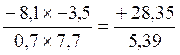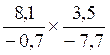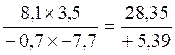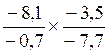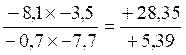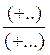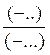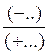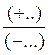multiplication avec deux écritures fractionnaires

Pré requis :

Fraction (nomenclature)
Voir évent. :Mettre une écriture fractionnaire sous forme de fraction
Multiplication de deux fractions de même dénominateur
Expression d' un résultat
Fraction irréductible
Arrondir "à tant prés" ;troncature

ENVIRONNEMENT du dossier :

Index warmaths

Objectif précédent

Objectif suivant

Tableau 153

Liste des cours sur les calculs sur les fractions et la multiplication…….

DOSSIER: MULTIPLICATION de deux écritures fractionnaires de dénominateurs différents.

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

COURS

Multiplication de deux écritures fractionnaires de même dénominateur:

exemple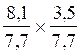

Voir niveau de difficulté 1 :

cette multiplication s ‘ opère de la même façon qu ‘ au niveau QV multiplication Niveau 1

CAS GENERAL qui est la multiplication de deux fractions (ou écriture(s) fractionnaire(s) .

La multiplication de deux fractions (ou écriture fractionnaire ) est égale à une troisième fraction (ou écriture fractionnaire ) qui aura pour:

Numérateur le produit des numérateurs

et pour

Dénominateur le produit des dénominateurs.

Ensuite : il suffit de mettre le résultat sous forme de fraction , et de mettre la solution sous forme de fraction irréductible ou sous forme décimale suivant le « rang » demandé.

Exercices	Résultats
	» 5,2597403
	» - 5,2597403
	» - 5,2597403
	» -5,2597403
	» - 5,2597403
	» + 5,2597403
	» +5,2597403
	» + 5,2597403
	» + 5,2597403

Rappel : division entre deux nombres relatifs
Traduction des règles en modèles mathématiques de la division d’un nombre relatif par un autre nombre relatif : * val : lire valeur absolue *Val₃ est un « rationnel »
Même signe : ( + val ₁ ) : ( + val₂) = ( + (val₁ : val₂) ) = + val₃ ( - val ₁ ) : ( - val₂) = ( + (val₁ : val₂) ) = + val₃	Sous forme fractionnaire : = (+……) = (+……)
Signe contraire : ( - val ₁ ) : ( + val₂) = (- (val₁ : val₂) ) = - val₃ ( + val ₁ ) : ( - val₂) = ( - (val₁ : val₂) ) = - val₃	Sous forme fractionnaire : = (-……) = (-……)

CAS : multiplication de deux écritures fractionnaires possédant des numérateurs et dénominateurs « relatifs »

Le produit	Devient l’opération suivante
-=	(+..) (+….)=
=	(+..) (+….)=
=	(+..) (+….)=
=	(-….) (+….)=
=	(-….) (+….)=
=	(-….) (+….)=
=	(-….) (+….)=

TRAVAUX AUTO FORMATIFS.

CONTROLE

A quoi est égale la multiplication de deux écritures fractionnaire?

EVALUATION

Exercices	Résultats

Rappel : division entre deux nombres relatifs