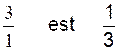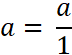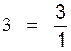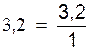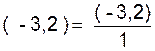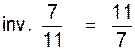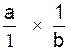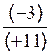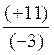Inverse d’un nombre :

On ne peut pas donner  l’inverse d’un nombre, mais  on donnera  l’inverse de la fraction qui le représente, cette fraction aura pour dénominateur « 1 » .

Procédure : faire l’inverse d’un nombre c’ est rechercher  l’inverse d’une fraction  dont le dénominateur vaut « 1 » :

Il n’y a aucun calcul à faire , il suffit de permuter les nombres de la fraction :

Ainsi l’inverse de 

  commentaire  :  on a besoin de l’inverse d’un nombre  (facteur )pour pouvoir neutraliser un facteur  se trouvant dans un terme.  ( exemple : 3  multiplié par  1/3  =  1 )

  Notation:

La notation mathématique  de « l’inverse » d’un « facteur   a » ,ou d’un  nombre  s’écrit  «  inv. a  ».

Ainsi  :

       Pour obtenir l’inverse d’un  nombre il  faut construire une fraction de numérateur égal à 1 et de dénominateur égal à ce nombre ;

Procédure permettant  d’obtenir l’inverse d’un nombre:

Activités :

Exemples numériques

1°) Savoir mettre le nombre sous forme de fraction de dénominateur  égal à  1 :

Avec un nombre entier :

Avec un  nombre décimal :

"

Avec un nombre relatif :

2) Savoir  « Inverser » les "termes" de la "fraction": ( on dit aussi « permuter » les termes de la fraction) . Il faut :

- a) mettre le numérateur en dénominateur (C à d. : descendre le nombre sous la barre de fraction)

 - b) et mettre le dénominateur au numérateur. (C à d. : remonter le nombre sous la barre de fraction , et le mettre à la place de celui qui a été déplacé)

        à pour inverse : 

     à pour inverse :  

 ;    à pour inverse :

3) savoir rendre compte :

l’ inv.  a  =

Inv. 3" =   

Inv. "3,2" = 

Inv. "(-3,2)" =   

Traduction littérale  :

 «  L’inverse de 3  est égale à la fraction   »   s’écrit      « inv.3 =     »

  Généralisation:     inv. a  =             

 (on peut écrire aussi :   1 / a ) ; (si « a » est différent de 0)

remarque : 0 n’a pas d’inverse

Niveau lycée :

Convention d’ écriture :    est équivalent à l’écriture  

Calcul de     ( avec n  désignant un nombre entier )

Cliquer ici pour consulter la Table numérique

0 <n  <  100

Prendre 10 nombres entiers compris entre  0 et 100  et  Calculer (avec la calculatrice )   ; comparer les résultats avec ceux donnés par la table ( attention : la table est un référent)

Pour en savoir plus cliquer ici. : la fonction homographique

Autres exemples:        

Info +++

Inv.x =

Inv.y = 

inv   - 3  =    1/ -3 =   

inv    2x  =  1 / 2x  =

Représentation graphique de l’inverse d’un nombre:

La représentation graphique d l’inverse d’un nombre est un point situé sur une ligne .

Soit l’inverse de « a »  =     1 / a       (que  « a » soit positif ou négatif ) le résultat est toujours inférieur à  1.

Remarque            :      inv. a / b    =    b / a

ce qui donne comme représentation graphique:

II  )    L'inverse d'une fraction ou écriture fractionnaire :

Niveau collège  (à  mettre en lien avec la division d’une fraction par une autre fraction)

L  ' inverse de la fraction         ,  ou  (a / b )  est égal à la fraction     soit  (b / a)

Ce qui se note :   inv         =   

Exemple :     

commentaire  : on a besoin de l’inverse d’une fraction dans le cas de la division d'un fraction par une autre fraction .

Voir  cours :   division de deux fractions

Info @ 

Nota:  si vous avez fait l’objectif sur la multiplication de deux fraction vous pouvez  savoir que : la fraction   =    

On dit que la fraction       est égale  à la multiplication du nombre "a" par l'inverse du nombre "b"  : on peut  écrire que     = a inv."b"

Procédure permettant de donner l'inverse d'une fraction: pour donner l'inverse d' une fraction  il suffit d'inverser le numérateur avec le dénominateur  , de la fraction.

Exercices exemples: 

Donner l 'inv.de ………

résultat

Inv.  =

Inv.     =

Inv.  =

Inv. 3  =

Inv.-    =

-

Travaux auto - formatifs :  (repris en devoir)

: TRAVAUX AUTO FORMATIFS.

CONTROLE:

I )  INVERSE:  (d’un nombre)

1)   A quoi va servir l’inverse d’un nombre?

2)    Traduire en langage mathématique:    inverse d’un nombre  « a »

3 )    Donner la procédure permettant d’avoir l’inverse d’un nombre.

4)   Traduire en langage littéral:

                                inv. a      =   inv.  a / 1    =   1 / a

II )  Inverse d’une fraction :

5)   A quoi va servir l’inverse d’une fraction ?

6)      Traduire :              inv. a / b    =    b / a

7 )    Donner la procédure permettant de donner   l’inverse d’une fraction

EVALUATION :

inv.(+ 4)   =   

inv. (5 / 3) =

inv.  (-  5) /(+ 3) = 

inv. (- 9) =       

inv.(+5)/(-3) =   

Niveau +  Utilisation de la calculatrice :

III ) compléter les égalités suivantes :

inv. x   =     

opp. x  =  

inv. a / b =

inv. ab / c =

inv. - x /3  =