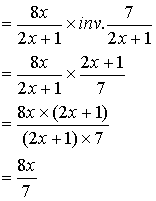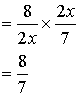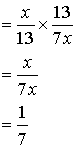|
|
Pré requis :
|
Fraction (nomenclature) |
|
|
Multiplication de deux fractions de
même dénominateur |
|
|
Expression d' un résultat |
|
|
Fraction irréductible |
|
|
Arrondir "à tant prés"
;troncature |
ENVIRONNEMENT du
dossier :
|
Tableau |
DOSSIER DIVISON de deux rationnels de
même dénominateur
.
A) Forme générale
B ) Procédure
pour diviser deux fractions de même
dénominateur:
C ) Procédure
pour diviser deux écritures
fractionnaires de même dénominateur:
|
TEST |
Interdisciplinarité |
|
Corrigé Contrôle |
Remarque
importante: Nous ne pouvons pas diviser
par une fraction , il faut
impérativement transformer la division
A) Forme générale
CAS GENERAL
:
La fraction de fractions doit être transformée en
division de deux fractions
Donc
l’écriture : 
se
transforme en 
La fraction de fractions 
devient 
A SAVOIR:
1°) La première fraction étant au dessus de la barre de fraction alignée avec le signe « égal » , la
deuxième fraction étant située sous la barre de fraction alignée avec le signe
égal,
2°) Bien que
la fraction de fractions soit transformée en division ; la division de deux
fractions ne se fait pas ; il faut la transformer en multiplication en
respectant des règles:
« Pour diviser deux fractions il suffit
de transformer la division en multiplication ,pour cela on multiplie la
première fraction par l’inverse de seconde fraction. »
Et
l’on applique ,ensuite, les règles de la multiplication de deux fractions.
|
Rappel
*: Inverse
de |
Objectif
: INVERSE
d'un nombre.(ou fraction) |
Procédure
permettant de faire la division de deux fractions:
1°) Identifier la première et la deuxième
fraction.
a )première fraction : 8 / 13
b) deuxième fraction :
7 / 11
2°) faire l’inverse de la deuxième
fraction:
inv 
= 
3° )construire l’égalité avec le premier
membre étant la division et le deuxième la transformation en multiplication.
4° ) Appliquer la procédure sur la multiplication de deux fractions: 
Modèle mathématique:
=
Objectif : QVI
division niveau .1
A ) Procédure pour diviser deux
fractions de même dénominateur:
Exemple :
= ?
On
respecte la procédure vu précédemment:
Procédure
permettant de faire la division de deux fractions : 
1°)
Identifier la première et la deuxième fraction.
a)
première fraction : 8 / 13
b)
deuxième fraction : 7 / 13
2°) Faire l’inverse de la deuxième
fraction:
inv 
= 
3° ) Construire l’égalité avec le premier
membre étant la division et le deuxième la transformation en multiplication.
4° )
Appliquer la procédure sur la
multiplication de deux fractions:
C )
Procédure pour diviser deux écritures fractionnaires de même dénominateur:
La procédure utilisée pour faire la division
de deux fractions s’applique à la division
de deux nombres écrit sous forme d’écriture fractionnaire. Objectif
: QVI division niveau.4
Par exemple
: on peut faire l’opération: 
qui donnera
Voici
trois cas :la soustraction s'opère de la même façon qu'avec un nombre de
dénominateur commun
|
|
|
|
a)
Sans autre difficulté |
|
|
|
|
|
b
) idem |
|
|
|
|
|
c
)idem |
|
|
|
|
=
=
TRAVAUX AUTO FORMATIFS.
Rappel . La multiplication de deux fractions (ou écriture fractionnaire ) n’est
possible qu ’ à une condition laquelle ?
1°)Traduire en langage littéral: =
2°)Traduire en langage mathématique:
I ): Effectuer les calculs suivants:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
II ) Faire les exercices suivants avec des nombres
décimaux
|
|
|
|
a) |
|
|
b) |
|
III ) Faire les exercices suivants
avec des nombres décimaux relatifs .
|
|
|
|
a)
|
|
|
b)
|
|
|
c) |
|
IV ) Faire
les divisions suivantes :
|
|
|
|
a)
|
|
|
b
) |
|
|
c
) |
|
V) Faire
les divisions suivantes :
|
|
|
|
a) |
|
|
b
) |
|
|
c
) |
|
VI) idem
|
a ) |
|
|
b ) |
|
VII ) Idem
|
a) |
|
|
b) |
|
VIII ) Faire les divisions suivantes : (pour pouvoir regrouper les termes en
numérateur il faudra revoir l’objectif
sur « Factoriser -
développer »
|
a
) |
|
|
b
) |
|
|
c
) |
|
|
d
) |
|
|
e
) |
|
