Pré requis:

La division par « zéro »

Les fonctions numériques ( généralités)

Les suites de Grandeurs proportionnels

Les notions sur les Grandeurs inversement proportionnelles

ENVIRONNEMENT du dossier:

Retour vers l’accueil « warmaths »

Objectifs précédents : 1°) calcul : l’inverse d’un nombre entier 2°) les tables numériques .(les 1/n) 3°),,Les grandeurs inversement proportionnelles .

Objectif suivant Niveau 5 : Les fonctions usuelles

1°)Sommaire sur : les grandeurs proportionnelles et inversement proportionnelles 2°) Sommaire sur : les études de fonctions

DOSSIER : LA FONCTION 1 /x ou ; la fonction homographique

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité : Arithmétique : les grandeurs inversement …………

Corrigé Contrôle

Corrigé évaluation

COURS

Les grandeurs inversement proportionnelles

INFO PLUS+++

Considérons un rectangle d’aire constante : 800 cm^2 et de dimension variables , mesurées en centimètres par « x » et « y » . La relation entre « x » et « y » peut s’écrire sous trois formes équivalentes : 1°) Forme 1 : xy = 800 2°) Forme 2 : y = ou 2°’) y = 800 3°) Forme 3 : = ou 3°’) x = 800 les relations 2’ et 3’ montrent que : y est proportionnel à , c’est à dire l’inverse de « x » x est proportionnel à c’est à dire l’inverse de « y »

FONCTION homographique : f : x

f : R R

x

1°) Ensemble de définition.

On ne peut diviser par 0 donc D_f = R^* = ] -¥ ;0[ È ]0 ; +¥ [

2°) Particularité : (est-elle paire ou impaire ? )

quel que soit le réel « x » appartenant à D_f f(-x) = = - = - f(x) ; f est donc « impaire »

3° ) Etude aux bornes du domaine de définition Df:

que se passe-t-il quand f (x) tend vers 0^- (lire zéro moins)?

f (x) tend vers 0 ^- quand « x » tend vers -¥

que se passe-t-il pour f (x) quand « x » tend vers -¥ ?

f (x) tend vers - ¥ quand « x » tend vers 0 ^-

que se passe-t-il pour f (x) quand « x » tend vers +¥ ?

f (x) tend vers +¥ quand « x » tend vers 0⁺

que se passe-t-il quand f (x) tend vers 0^+- (lire zéro plus)?

f (x) tend vers 0⁺ quand « x » tend vers +¥

c) que se passe-t-il pour f (x) quand « x » = 0

f (o) = impossible

d) résoudre  f (x) = o 0 = donc x =

4°) Sens de variation :

le coefficient de est positif « a » = 1

f est donc strictement décroissante sur R^- et strictement croissante sur R⁺

5°) le tableau de variation :

x	-¥ 0 +¥
f(x)	0 ^- + ¥ -¥ 0 ^-

La double barre indique que f(x) n’existe pas pour x=0

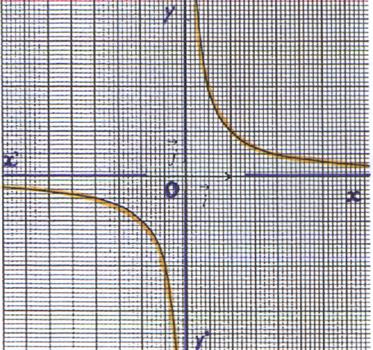
6°) Représentation graphique : La représentation graphique de la fonction f est l’ hyperbole d’équation y = admettant les axes ( x’x ) et ( y’y) comme asymptotes et le point O ( 0 ; 0 ) comme centre de symétrie .

Fonction se déduisant d’une fonction usuelle par addition d’une constante.

Soit b un nombre réel et une fonction numérique f de R vers R.

Les fonctions x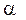f(x) et x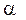f(x)+b ont le même sens de variation.

La courbe représentant la fonction x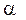f(x)+b se déduit de celle représentant x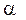f(x) par la translation de vecteur b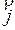

Exemple : f : R R

x+2

Sens de variation :

f a même sens de variation que x  ; elle est donc strictement décroissante sur ] -¥ ;0[ et sur ]0 ; +¥ [

le tableau de variation :

x	-¥ 0 +¥
f(x)	0 ^- + ¥ -¥ 0 ^-

La double barre indique que f(x) n’existe pas pour x=0

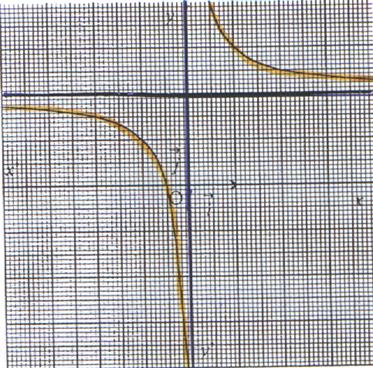
6°) Représentation graphique : La représentation graphique de la fonction f s’obtient à partir de celle de x par la translation de vecteur 2 La représentation graphique de la fonction f est l’ hyperbole d’équation y = +2 admettant la droite d’équation y =2 et l’ (y’y) comme asymptotes et le point de coordonnées ( 0 ;2 ) comme centre de symétrie .

TRAVAUX AUTO FORMATIFS.

CONTROLE:

1. Donner le modèle d’équation d’un fonction inverse ; dite homographique

2. Donner l’allure de la représentation graphique d’une fonction inverse .

EVALUATION: