|
|
|
|
Multiplication
d’une fraction par un nombre |
ENVIRONNEMENT du dossier:
|
Objectif précédent |
Les grandeurs proportionnelles (présentation) |
||
|
|
|
|
|
|
|
|
|
|
DOSSIER :
Notion sur
LES GRANDEURS « directement » ou les grandeurs
« inversement » PROPORTIONNELLES
|
|
|
|
|
|
|
|
|
|
|
|
Travaux auto formatifs |
|
|
|
|
|
|
TEST |
COURS |
Devoir Contrôle |
Devoir
évaluation |
Interdisciplinarité
|
|
Corrigé
Contrôle |
Corrigé
évaluation |
Définitions basiques
Des rapports et des
proportions :
Tous
ce que l’on peut découvrir sur les grandeurs se réduit à les exprimer les unes
par les autres , en les comparant ; cette
comparaison , qui ne peut jamais avoir lieu qu’entre des quantités de même
espèce ; détermine le rapport que ces quantités ont entre elles .
Il y a
deux manières d’établir un rapport :
Si
l’on compare , par exemple , 15 et 5 , en
retranchant 5 de 15 , on reconnaît que
le plus grand nombre surpasse de 10 le plus petit . Dans ce cas
, on détermine un rapport de différence .
Mais
au lieu d’une soustraction on opère une division , on
reconnaît que le plus grand nombre contient trois fois le plus petit , ou , ce
qui revient au même , que le plus petit est contenu trois fois dans le plus
grand , et , dans ce cas , on détermine un rapport par quotient .
C’est
ce dernier « rapport » que nous utilisons pour la suite de tous les
cours.
Rapport
« direct » ou « inverse » :
Deux
choses sont en rapport lorsqu’elles dépendent l’une de l’autre
, lorsque pour déterminer l’une
avec un degré de précision quelconque , l’autre doit nécessairement être
connue .
Un
rapport peut être direct ou inverse ; il est direct ,
lorsque les liaisons qui existent entre les deux quantités que l’on compare
sont telles que l’augmentation de l’une
occasionne nécessairement l’augmentation de l’autre ; il est
inverse lorsque l’augmentation de l’une occasionne nécessairement la diminution
de l’autre .
Ainsi
, dans
cet énoncé : quatre ouvriers ont fait
Il est
clair que plus il y aura d’ouvriers , plus ils feront
d’ouvrage : donc le produit de l’ouvrage augmente en proportion de
l’augmentation du nombre d’ouvriers , et conséquemment le rapport de l’ouvrage
est direct avec celui des ouvriers .
Dans
ce nouvel énoncé : quatre ouvriers seraient 8 jours pour faire un certain ouvrage , combien faudrait- il de temps à 6 ouvriers pour
faire le même ouvrage ? On voit que
plus il y aura d’ouvriers , moins ils seront de
temps : donc une augmentation dans le nombre des ouvriers donne une
diminution dans le temps , et conséquemment le rapport qui existe entre le
nombre d’ouvriers et l’ouvrage fait est inverse .
Le rapport :
Le
rapport qui existe entre deux quantités est le quotient de la première , divisé par la seconde .
En
comparant 5 et 6 ; 5 et 6 sont les deux termes du rapport : 5 est l’antécédent , 6 le conséquent , et le rapport entre ces
deux nombres est 
= 5/6 ; conséquemment de deux quantités en rapport , la
première est le dividende , la deuxième le diviseur , et le quotient exprime le
rapport ; deux nombres en rapport sont donc une division indiquée d’une
manière abrégée : le dividende est l’antécédent , le diviseur le conséquent , et la division
abrégée , réduite à sa plus simple expression , est le rapport qui existe entre
ces deux nombres. En comparant cette définition
à celle de la fraction , on reconnaîtra qu’il
n’y a pas de différence entre une
fraction et l’expression qui indique que deux nombres sont en rapport , et que
conséquemment l’un de l’autre doivent jouir des mêmes propriétés : donc ,
1°) En
multipliant ou en divisant l’antécédent (dividende) par un nombre , sans toucher au conséquent
(diviseur) , le rapport est multiplié ou
divisé par le même nombre .
2°) En
multipliant ou divisant le conséquent ( diviseur),
sans toucher à l’antécédent ( dividende) , le rapport est divisé ou
multiplié par le même nombre .
3°)En multipliant ou divisant
l’antécédent (dividende ou numérateur)
et le conséquent ( diviseur ou dénominateur) par le même nombre , le
rapport ne change pas .
4°)En divisant l’antécédent (dividende) par le rapport , lors même qu’il serait réduit à sa plus simple expression , on obtient le conséquent .
5°)
Lorsque l’antécédent et le conséquent sont égaux , le
rapport est l’unité .
6°)Lorsque
l’antécédent ( dividende ) est
plus grand que le conséquent , le rapport est plus grand que l’unité .
7°)
Lorsque l’antécédent ( dividende ) est
plus petit que le conséquent , le rapport est plus petit que l’unité .
8°)
lorsque le conséquent ( le diviseur ) est l’unité , le rapport est égal à l’antécédent (
dividende ) .
9°) Et
lorsque l’antécédent est l’unité , la plus simple expression du rapport est
égale à l’antécédent , divisé par le conséquent , c’est à dire que relativement
à la 8ème et 9ème propriété , le rapport de 
La proportion :
Lorsqu’en
comparant quatre quantités , le rapport qui existe entre la première et la
seconde est le même que celui qui existe entre la troisième et la quatrième ,
les quatre quantités forme une proportion *,donc toutes les fois que deux
fractions peuvent être ramener à une expression commune , sans rien changer à
leur valeur , elles forment ensemble une proportion ; donc 
et 
forment une
proportion ; parce que l’une et l’autre peuvent être ramenées à l’expression
commune 
; donc 9 ;3 ; 12 et 4 , forment une
proportion. Pour indiquer cette proportion , on
l’écrit ainsi ; 9 : 3 : : 12 : 4 et l’on
prononce ; 9 sont à 3 comme 12 sont à 4, d’où il en résulte que toutes
proportions sont composées de quatre termes : le premier et le dernier
s’appellent les extrêmes , le deuxième
et le troisième s’appellent les moyens ; mais deux fractions qui
peuvent de réduire à la même expression
sont égales : donc la proportion 9 :3 : :12 :4 peut se
représenter par = . Cette expression
nous conduira à trouver et à démontrer
les propriétés dont jouissent les
nombres en proportion . D’abord ,
on voit que le premier terme , divisé par le second , est égal au
troisième , divisé par le quatrième : donc , quel que soit le terme
inconnue d’une proportion , on le détermine toujours au moyen des trois
autres. Supposons que le premier terme
est inconnu , on aura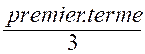 
= = 3 , et si le 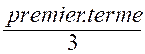= 3 , le premier terme sera
3
3 = 9 ; car le quotient d’une division , multiplié par
le diviseur , = le dividende .
Supposons
maintenant que le deuxième terme est inconnu, on aura 
= = 3 ; = 3
, le deuxième terme est = 3 , car le dividende divisé par le
quotient est égal au diviseur @ .
Or , si = , il est évident
que = ; donc la transposition des deux rapports ne trouble
point leur égalité ; donc les 3ème et le 4ème termes
étant inconnus , en transposant les deux rapports , on les déterminera comme il
vient d’être indiqué .
* en parlant de
rapports et de proportions , sans énoncer leur nature
, il est toujours sous – entendu qu’il est question de rapports et de
proportions par quotient.
Maintenant
, dans l’expression
= , le numérateur de la 1ère fraction est le 1er
extrême , et le dénominateur est le 1er moyen. Le numérateur de la 2ème
fraction est le deuxième moyen , et le dénominateur le
deuxième extrême ; or , l’on sait
que pour former une proportion ,
les deux fractions doivent pouvoir être réduite à la même expression , ce qui
revient à les réduire au même dénominateur et au même numérateur . Dans ce cas
, il faut que le numérateur de la première , multiplié par le dénominateur de
la seconde , soit égal au numérateur de la deuxième , multiplié par le dénominateur de la
première ; mais le numérateur de la première et le dénominateur de la seconde sont les
extrêmes , et le numérateur de la deuxième et le dénominateur de la première
sont les moyens : donc le produit des extrêmes est égal à celui des
moyens ; donc , pour que quatre nombres
soient en proportion , il faut que le produit des extrêmes soit égal au produit des moyens ; car si
cela n’était point , les deux fractions qui expriment les rapports de ces
nombres ne pourraient se réduire à la même expression , les quotients seraient
inégaux , et conséquemment la proportion n’existerait point .
Recherche
d’un des termes d’une proportion :
De
l’égalité du produit des extrêmes et du produit des moyens ,
il est facile de déduire une autre méthode
pour déterminer l’un des termes
inconnus au moyen des trois autres. En supposant successivement que le 1er
extrême ; le 1er moyen , le 2ème
moyen et le 2ème extrême sont inconnue , on aura :
Le 1er
ex. 4 = 3 12 = 36 ; donc le 1er
. = 
= 9
94 ou 36 = 1er
moy. 12 ; donc le 1er moyen = = 3
9 4 ou 36 = 3 le 2ème moy. ; donc le 2ème
moy. = 
= 12
9le 2ème ex. = 312 = 36 ; donc le 2ème extrême =
= 4
d’où
il en résulte que trois termes d’une proportion
étant connus , on trouve le
quatrième en divisant le produit des extrêmes par le moyen connu , ou le produit des moyens par l’extrême
connu , suivant que le terme dont on veut déterminer la valeur est un moyen ou un extrême .
La
théorie des fractions ferait encore découvrir une infinité de propriétés
applicables aux proportions. Cette théorie n’est pas à connaître si on se limite à l’arithmétique
, en effet cette théorie n’a pas d’application en arithmétique.
COURS
Approches : si l’on observe des objets
semblables mais de différentes grandeurs , on peut exprimer la relation ou la
proportion qui existe entre eux .
Il
existe une proportion entre le poids d’un objet et son volume ; entre le
prix d’un objet et sa grandeur ( masse , capacité , longueur, …) ; entre
un travail et le temps mis pour le
réaliser . Il existe une relation entre la distance parcourue en un temps donné
et la vitesse de la marche ; entre le temps nécessaire pour faire un devoir et la longueur de ce devoir .
Toutes
ces grandeurs sont dites : directement proportionnelles .
Au
contraire , que plus on marche vite ,
moins de temps on mettra à parcourir une distance ; que plus on écrit vite
, moins de temps il faudra pour écrire une page ; que plus on emploie
d’ouvriers , moins de temps on mettra
pour faire un ouvrage ; plus un champ rectangulaire est long , moins il sera large pour une même
superficie ,… Toutes ces grandeurs sont dites : inversement proportionnelles.
NOTION de « Quantités
proportionnelles »
|
Deux
quantités varient souvent dans le même rapport : si l’une croît ou diminue , l’autre augmente ou diminue dans le même
rapport : ainsi le prix d’une marchandise croît avec la quantité ( masse ,
capacité , longueur, …) ; le salaire avec les journées de travail ;
le temps nécessaire pour effectuer un parcours en fonction de la vitesse
moyenne ;…
Un
salarié en 5 jours gagnera cinq fois plus qu’en un jour et de fois moins qu’en dix jours ;
DEFINITION :
Deux grandeurs qui dépendent l’une
de l’autre sont directement proportionnelles lorsque , l’une d’elles devenant 2 ;
3 ; 4 ; … ;n fois plus grande
ou plus petite , l’autre devient , 2 ; 3 ; 4 ; … ;n
fois plus grande ou plus petite.
Exemples : Plus on emploiera de salariés pour faire un travail , moins de temps on mettra ;
la vitesse d’un train est inversement proportionnelle à la durée du trajet . Le
nombre de journées nécessaires pour accomplir un ouvrage est inversement
proportionnel au nombre d’heures de travail par jour , etc.
Définition : deux grandeurs
qui dépendent l’une de l’autre sont
inversement proportionnelles lorsque , l’une d’elles devenant 2 ; 3 ;
4 ;… n fois plus grande ou plus petite , l’autre devient en même temps 2 ; 3 ; 4 ;… n
fois plus petite ou plus grande .
Les grandeurs proportionnelles permettent de
résoudre un grand nombre de problèmes pratiques tels que les calculs des
salaires , des prix , des intérêts , de l’escompte , des bénéfices , des
alliages et répartitions proportionnelles , des impôts , etc.
Dans la plupart des cas ,
elles se résolvent au moyen de la « règle de trois » .
Dans le calcul des grandeurs proportionnelles ,
les rapports peuvent être
plus ou moins nombreux et se combiner entre eux
de divers façons donnant tantôt des
proportions directes , tantôt des proportions inverses . Il importe
pour ne pas se tromper de faire attention à la nature de ces divers rapports.
1°) Quand dit-on que deux grandeurs sont
proportionnelles ?:
2°) Quand dit-on que deux grandeurs sont
inversement proportionnelles ?:
1°) Si deux
livres coûtent 56 francs ; combien coûteront trois livres ;
sept livres ; dix livres ?
2°) Un salarié gagne