Pré requis:

Nombres proportionnels
notions : Les grandeurs « directement » ou « inversement » proportionnelles .
Pré requis sur les fractions :
Fraction nomen clature
Fraction équivalente
Produit en croix

ENVIRONNEMENT du dossier :

Objectif précédent :

1°) vu en primaire.

2°) Idée de la proportionnalité.

3°) La proportion et la quatrième proportionnelle

4°) Fiche pédagogique collège : la proportionnalité et les pourcentages..

Objectif suivant :

1°) Les grandeurs proportionnelles (sommaire)

2°) Cours niveau V

3°) la proportion en algèbre .

tableau 171

liste des cours sur les proportions ; grandeurs proportionnelles et inversement proportionnelles

DOSSIER : LA PROPORTION

1. LES SUITES DE NOMBRES PROPORTIONNELS

2. le coefficient de proportionnalité.

3. Application aux GRANDEURS PROPORTIONNELLES

4. le partage proportionnel

5. les travaux auto formatifs.

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité :

Situations problèmes

Corrigé Contrôle

Corrigé évaluation

On établit en arithmétique ces deux principes :

· Pour que deux grandeurs soient proportionnelles l’une à l’autre, il faut et il suffit qu’elles varient dans le même rapport ; c'est-à-dire que si l’une devient « n » fois plus grande qu’elle n’était, l’autre devienne aussi « n » fois plus grande.

· Pour que deux grandeurs soient inversement proportionnelles l’une à l’autre, il faut et il suffit qu’elles varient dans le rapport inverse ; c'est-à-dire que si l’une devient « n » fois plus grande qu’elle n’était, l’autre devienne aussi « n » fois plus petite qu’elle n’était.

COURS

@ info

1° ) Suites de "nombres proportionnelles" :

Deux suites de nombres « S_{1 » =}{ ( y₁ ; y₂ ;y₃ ; ....)} et « S₂» »= {( x₁ ;x₂;x₃x ;......)} forment une suite de nombres proportionnels si elles forment une suite « S_proport. » de rapports égaux .

important : remarquer que la première suite contient les éléments « y », par convention.

Traduction mathématique :

S_proport. = si ===.........

2°) COEFFICIENT DE PROPORTIONNALITE :

Info plus ! ! !

Nous pouvons constater que les rapports d’un nombre (y ) ,de la première suite, sur le nombre ( x ) de la deuxième suite ,de même rang (exemples ou ... ) .donne un même nombre ,on dit que le « rapport » est constant . (voir « rapport égaux » )

ce nombre s’appelle « coefficient de proportionnalité».

On appelle « coefficient de proportionnalité » le nombre constant représentant la valeur commune de tous les rapports de deux suites de nombres qui forment une suite de nombres proportionnels.

Le coefficient se notera toujours par la lettre « k ».

Donc si S1 (première suite ) et S2 ( deuxième suite) sont des suites de nombres qui forment une suite de nombres proportionnelle alors le rapport de S1 sur S2 est égal à « k ».

Traduction mathématique :

si = k alors S1 et S2 sont deux suites qui forment une suite de rapports égaux.*

@ Info1 ;@ info 2:

3°) APPLICATIONS AUX GRANDEURS PROPORTIONNELLES

Sciences :

Définition de « grandeur » :on appelle « grandeur » un nombre associé à une unité de mesure.

Lorsque deux grandeurs de nature différentes : ( exemples un prix en fonction de la masse soit des mesures en kg et f ); si elles varient en même temps dans un même rapport (exemple 10 francs pour un kilogramme , noté : 10 fr.kg^-1 ) ,on dira que nous avons des grandeurs proportionnelles.

Exemple : nous achetons différentes quantité d’un même produit , le prix étant fonction de la masse achetée. ( l’unité de prix est l’euro (symbole : € ; l’unité de masse est le kilogramme : kg )

On établi le tableau suivant :

S ₂ les (x)	*Masse en kg*	0,830	1,240	1,850	2,320
S ₁ les (y )	Prix en € .	26,56	39,68	59,20	74,24

Considérons les suites S1 et S2

S1 = { 26,56 ; 39,68 ; 59,20 ; 74,24 }

S2 = { 0,830 ; 1,240 ;1,850 ;2,320 }

Activités : (faire le calcul de chaque « rapport » : 26,56/0,830 = 32 ; 39,68 /1,240 = 32 ; .........)

si nous calculons tous les rapports de ,( nous ne sommes pas intéressés par S₂/ S₁) ; nous trouvons pour chaque calcul le nombre « 32 » .

Conclusion : Nous constatons que nous avons un « même » nombre , ce nombre se nommera « coefficient » ,dans tous ces cas ce coefficient portera le nom de « coefficient de proportionnalité »

si = k alors S1 et S2 sont deux suites qui forment une suite de rapports égaux.

Les rapports étant des nombres, les résultats étant constants , ces nombres étant des grandeurs , nous dirons que « ces grandeurs sont proportionnelles ».

Nous dirons :

que deux grandeurs sont « proportionnelles » si les mesures de chacune d’elles forment une suite de rapports égaux.

4°) PARTAGES PROPORTIONNELS :

Rappels :INFO sur les notions

Problèmes types :

Problème N° 1 :

Partager 155 en parties proportionnelles aux nombres 9 ; 12 et 10 .

Partager 155 en parties proportionnelles aux nombres 9 ; 12 et 10 c’est trouver trois nombres qui aient pour somme 155 et qui soient proportionnels à 9 ; 12 et 10.

Il est évident que si la somme à partager était 9 ; 12 et 10 = 31

On peut donc raisonner comme suit :

1°) lorsque la somme à partager est 31 la 1^re à 9

lorsque la somme à partager sera de 155 la 1^re aura « x » donc

x = =45

2°) lorsque la somme à partager est 31 la 2^e à 12

lorsque la somme à partager sera de 155 la 2^e aura « x » donc

x = =60

3°) lorsque la somme à partager est 31 la 3^e à 10

lorsque la somme à partager sera de 155 la 3^e aura « x » donc

x = =50

les trois nombres sont respectivement 45 ; 60 et 50

Règle : pour partager un nombre proportionnellement à des nombres donnés , on le divise par la somme de ces nombres et l’on multiplie le quotient trouvé successivement par chacun des nombres donnés .

Problème N° 2 : On veut partager 2400 proportionnellement aux nombres 7 ; 8 et 9.

Exemple d'application: 3 personnes ont gagné aux courses 2 400 € , la première a misé 7 € , la seconde 8 € et la troisième 9 € .Les gains sont répartis proportionnellement aux mises , combien recevra chaque personne .

Résolution :

(penser à diviser en trois parts ,mais dont le premier à les 7 parts du total des parts ,le deuxième à 8 parts du total des parts et ainsi de suite.......)

On veut donc déterminer trois nombres x ;y ; z tels que :

x + y + z = 2400 et que

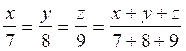==..100

Donc 100 soit x = 700

=100 soit y = 800

=100 soit z = 900

Le partage doit s ‘effectuer suivant les nombres 700 ; 800 ;900

TRAVAUX FORMATIFS :

CONTROLE :

1. Donner un exemple d’une suite de nombres.

2. Citer deux suites de nombres qui ne forment pas une suite de rapports égaux.

3. Citer deux suites de nombres qui forment une suite de rapports égaux.

4. A quoi est égale le rapport de deux suites de nombres proportionnels ?

5. Donner le modèle mathématique représentant le rapport de deux suites de nombres proportionnels.

6. Q’ appelle - t - on : « coefficient de proportionnalité »

7. par quelle lettre le désigne -t - on ?

8. Qu ’ appelle -t -o n « grandeur » ?

9. Quand dit - on que deux grandeurs sont proportionnelles ?

10. Quand dit - on que deux grandeurs ne sont pas proportionnelles ?

11. Que faut - il pour que deux grandeurs soient proportionnelles ?

12. On nomme : S_{1» =}{ ( y₁ ; y₂ ;y₃ ; ....)} et S_2 = {( x₁ ;x₂;x₃ ;......)} que faut - il pour que les deux suites représentent deux suites de nombres proportionnels ?

13. Que signifie l’écriture : = k

EVALUATION :

1° ) Les deux suites [ 9 ;11 ;19 ;25 ;31 ;] et [27 ; 33 ;57 ;75 ;93 ;] sont - elles des suites de nombres proportionnelles ?

2°) Même question : pour : [ 7 ;13 ;17 ;28] et [ 77 ;130 ;180 ;309 ]

3°) Même question pour [5,2 ;7,9 ;13,4 ;18,9] et [ 21,84 ;33,18 ;56,28 ;79,38 ]

4°) A et B étant des grandeurs directement proportionnelles , compléter le tableau :

Mesure de A	.	21	35		70	280
Mesure de B	2		10	18			200

5°) Compléter les deux suites de nombres proportionnelles : [9 ;13 ;x ;17 ;31 ] et [ 117 ;169 ;195 ;y ;403]

6°) compléter le tableau suivant (les nombres de la première suite sont proportionnels aux nombres de la deuxième suite) :

a	50	70	90	d
0.5	2	b	c	10

7°) Idem.

10		15		27
	2.2	3	4.8

8°) La suite de nombres [a ;b ;c ;d] est proportionnelle à la suite de nombres [3,5 ;5,7 ;4 ;9] .Le coefficient de proportionnalité est 3 . Calculer a ;b ;c ;d

9°) Même question pour les suites [a ;b ;c ;d] et [9 ;17 ;36 ;52].Le coefficient de proportionnalité est de 0,75.

INTERDISCIPLINARITE

PROBLEMES :

A ) La longueur du cercle est donnée en fonction du diamètre ; compléter le tableau suivant :

D	5	10	12	25	28.2
L

Les deux grandeurs sont-elles proportionnelles ?

B ) Un cycliste parcourt 12km en 45mn .Un autre 17km en 50mn .Les distances parcourues sont-elles directement proportionnelles aux durées du parcours ?

C ) Construire un triangle ABC dans lequel BC = 50mm , l’angle B =40° et l’angle C =50°

Mesurer les cotés et les angles. Les mesures des cotés sont-elles proportionnelles aux mesures des angles opposés ?

D ) Même question pour un triangle ABC tel que l’angle A = 60° , l’angle B = 30° ,AB =70mm

E ) Une voiture se déplace à la vitesse constante de 80 km.h^-1 .La distance parcourue est-elle proportionnelle à la durée du parcours ?

F) Trois associés ont investi dans la même entreprise :le premier :10 000 € ,le deuxième : 14 000 € ;le troisième :26 000 €. Ils ont gagné 13 680 €

Partager le gain proportionnellement aux mises des associés .

G) 10 copropriétaires doivent se partager des frais de réfection s’élevant à 26 400 € , proportionnellement au montant de la valeur locative de leur appartement, s’élevant respectivement à :

200 € ;220 € ;250 € ; 300 € ; 350 € ; 400 € ; 500 € ;530 €

Quelle doit être la part de chacun ?

H ) Les copropriétaires d’un immeuble répartissent 8 000 € de travaux exécutés à frais communs proportionnellement à la valeur locative de leurs appartements estimée comme suit :

quatre appartements à 75 € ; 5 à 60 € et 10 à 40 €. Calculer le montant des frais qui incomberont à chacun.

Corrigé interdisciplinarité :