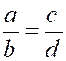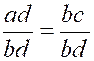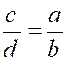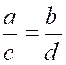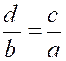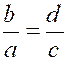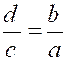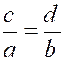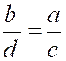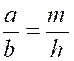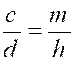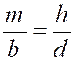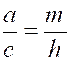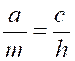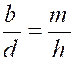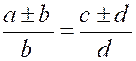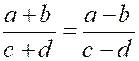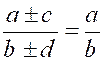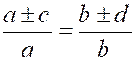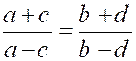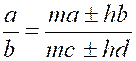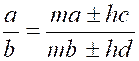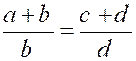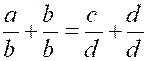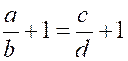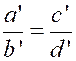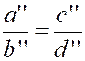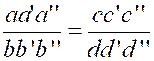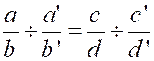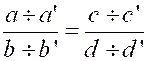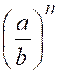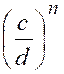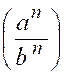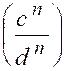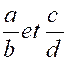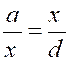Pré requis
|
|
ENVIRONNEMENT du dossier :
|
Objectif
précédent : |
Objectif suivant : |
|
||
|
INFORMATIONS : Module : calcul algébrique
|
||||
LES
CALCULS FRACTIONNAIRES : LES
PROPORTIONS algébriques
.
· Définitions.
( rapport ; proportion)
· Propriétés généralités des proportions. ( les 6 théorèmes
)
· Problèmes.
|
|
|
Travaux
auto formatifs. |
|
|
Corrigé |
||
|
TEST |
COURS
|
Interdisciplinarité :
|
|
||||
|
|
|
|
|
|
Définitions : |
|
|
« Rapport » : On
appelle « rapport
géométrique » de « a » à « b » ; ou
simplement « rapport » de « a » à « b » ;
l’expression « a : b » ou « « Rapports » ;
« fractions » et « quotients » sont choses identiques en
algèbre. Il
en résulte qu’on doit appliquer aux rapports le principe fondamental des fractions
algébriques , avec toutes ses conséquences. On
peut , sans altérer la valeur d’un rapport ,
multiplier ou diviser les deux termes par une même quantité. |
|
|
|
|
Deux
rapports : |
|
|
|
Proportions : On appelle
« proportion
géométrique » , ou simplement « proportion » , une égalité
entre deux rapports. Ex : |
|
|
|
Les
dividendes ou numérateurs « a » et « c » s’appellent les
« antécédents » ; les diviseurs ou dénominateurs
« b » et « d » , les
« conséquents » ; « a » et « d » sont les
« extrêmes » et « b » et « d » sont les
« moyens ». |
|
|
|
On
énonce souvent une proportion, surtout en géométrie ,
en disant : « a » est à « b » comme « c »
est à « d ». Chacun
des quatre termes d’une proportion est une « quatrième
proportionnelle » par rapport aux trois autres termes., Une
proportion dont les moyens sont égaux est dite « continue » et le
terme moyen s’appelle la « moyenne géométrique » ou la
« moyenne proportionnelle » entre les termes extrêmes. Chacun des
extrêmes est alors une « troisième proportionnelle » par rapport à
l’autre extrême et à la moyenne. |
|
|
|
Ainsi , la proportion |
|
|
|
Propriétés générales des proportions. |
|
|
|
|
|
|
|
Théorème 1 : la condition nécessaire et suffisante pour que quatre quantités
« a ; b ; c ; d »soient en proportion est que le
produit des extrêmes soit égal au produit des moyens. |
|
|
|
1°)
En effet , soit
|
|
|
|
2°) Réciproquement ,
soit « ad = bc » : divisant de part
et d’autre par « bd » , on a : |
|
|
|
|
|
|
|
Corollaires : N°1 : Toute égalité
entre deux quotients peut se transformer en une égalité entre deux produits,
et réciproquement. |
|
|
|
N°2 : On peut
faire subir à une proportion toutes les transformations qu’on voudra , à la condition que le produit des extrêmes reste
constamment égal au produit des moyens. |
|
|
|
|
|
|
|
N° 3 : Dans une
proportion, on peut : 1°)
intervertir l’ordre des rapports ; 2°)
échanger les moyens ; 3°)
échanger les extrêmes ; 4°)
remplacer chaque rapport par son inverse. L’équivalence entre
|
|
|
|
Quant
aux autres transformations
, considérons la proportion : des
proportions : |
|
|
|
Remarque :
Le second théorème permet d’écrire , sous huit
formes différentes, une même proportion. |
|
|
|
|
|
|
|
|
|
|
|
Théorème 3 : Si deux proportions ont un rapport commun ,
les deux autres rapports forment proportion. |
|
|
|
Les
égalités : |
|
|
|
|
|
|
|
Remarque :
De même , si l’on a
|
|
|
|
|
|
|
|
Théorème 4 : l’une quelconque des proportions suivantes ,
ou de celles qu’on peut obtenir par l’inversion des extrêmes et des moyens,
entraîne toutes les autres. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
On
peut établir ce théorème de diverses manières. |
|
|
|
Par
exemple, soit à démontrer l’équivalence entre : |
|
|
|
D’où :
On
établirait encore cette équivalence , en montrant que l’une et l’autre proportion
fournissent la même égalité « ad =
bc » entre le produit des moyens. |
|
|
|
|
|
|
|
Théorème 5 : En multipliant terme à terme plusieurs proportions ou en divisant
terme à terme deux proportions , on obtient une
nouvelle proportion. |
|
|
|
|
|
|
|
En
effet, les égalités |
|
|
|
|
|
|
|
Les
deux premières égalités, divisées membre à membre ,
donnent |
|
|
|
|
|
|
|
Théorème 6 : En valeurs absolues , les puissances ou les
racines de même degré des quatre termes d’une proportion forment une
proportion. |
|
|
|
|
|
|
|
En
effet : 1°)
l’égalité d’où
|
|
|
|
2°)
Les puissances « nième »
de |
|
|
|
|
|
|
|
SITUATIONS PROBLEMES. |
|
|
|
|
|
|
|
N°1 Trouver l’un des quatre termes d’une proportion , connaissant les trois autres. |
|
|
|
Réponse : la relation fondamentale « ad = bc » conduit aux règles suivantes : 1°) Pour obtenir une « terme extrême »
, on divise le produit des moyens par le terme extrême déjà
connu : car on a « a = 2°) Pour obtenir un
terme moyen , on divise le produit des extrêmes par
le terme « moyen » déjà connu ; car on a « b = |
|
|
|
|
|
|
|
N°1 Trouver la moyenne géométrique entre deux quantités. |
|
|
|
Pour obtenir la moyenne géométrique entre deux quantité données on extrait la racine carrée du produit de
ces quantités. Car la proportion continue
|
|
|
|
|
|
|
Rappel : En géométrie , on
établit qu’un rectangle de largeur « a » et de longueur
« b » est équivalent en surface à un carré ayant pour côté «
x = Par
généralisation , on appelle « moyenne
géométrique » entre « n » quantités « a ; b ;
c ; d ; e ; … » une quantité « x » |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|