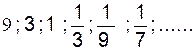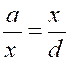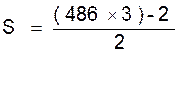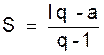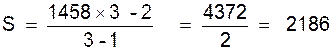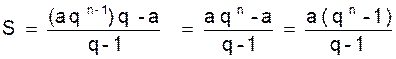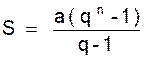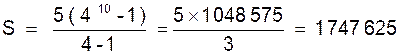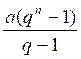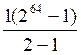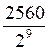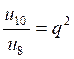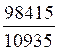|
|
|
|
Suites
arithmétiques |
ENVIRONNEMENT du
dossier:
|
tableau |
DOSSIER : Les Suites
« ou progression »
géométriques
I ) Définition d’ une PROGRESSION GEOMETRIQUE :
II ) RECHERCHE DU Nème TERME.
III ) MOYENNE
GEOMETRIQUE
IV ) RECHERCHE DE LA SOMME
DES TERMES d’une progression géométrique limitée.
V) Insérer « n » moyens géométriques
|
TEST |
COURS |
Interdisciplinarité |
|
► La
suite de nombres U = 2000 ; 2400 ; 2880 ; ….. représentant les
productions annuelles d’une entreprise est obtenue par multiplication
successives par « 1,2 » ; c’ est une suite géométrique. (l’augmentation de
la production annuelle est de 20% l’an)
► Les nombres 1 ;
2 ; 4 ; 8 ; 16 ; 32 ; 64 ;.. forment une progression géométrique de raison
« 2 ».
► Les
nombres 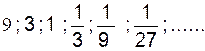 forment une suite géométrique de raison
forment une suite géométrique de raison ![]()
@ ( si problème sur
le calcul revoir la
multiplication d’une fraction par un nombre ou la multiplication de deux
fractions de dénominateur différent)
I ) Définition
d’ une PROGRESSION GEOMETRIQUE :
Définition :
Une progression géométrique est une suite de termes tels que chacun d’eux est égal à celui qui le
précède, multiplié par une quantité constante appelée « raison :
q »
|
Si « u » est la suite géométrique de premier terme u1 = a
et de raison « q » Soit « n » entier supérieur ou égal à 2
u1 = a u2=u1 u3=u2 u4=u3 u n= u n-1_ |
Le quotient de deux termes consécutifs est évidemment constant et égal à
la raison .
On appelle aussi les progression géométriques :
« progression par quotient ».
Exemples :
(1) 2 ; 6 ; 18 ;
54 ; …………. ;
n ; 3 n ;…… est
une progression géométrique croissante de raison « 3 ».
(2) 25 ; 5 ; 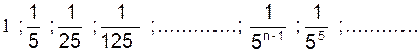 est une progression
géométrique croissante de raison «
est une progression
géométrique croissante de raison « ![]() ».
».
( 3 )
- 6 ; + 12 ; - 24 ; + 48 ; ………. ; +
n ; - 2n …………. est une progression géométrique
croissante de raison « -2 ».
Généralisons :
«
La progression est croissante ou décroissante ,
suivant que la raison est plus grande ou plus petite que l’unité.
|
Si r >1 : la progression géométrique est croissante : Exemple ► les nombres 1 ; 2 ; 4 ; 8 ; 16 ; 32 ; 64 ;..
forment une progression
géométrique de raison « 2 ». |
|
Si r < 1 : la
progression géométrique est décroissante. ► les
nombres |
« r < 0 : ??? » On pourrait considérer comme progressions géométriques des suites de
termes telles que :
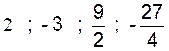
dont la raison serait : ![]() ; On remarque que lorsque la raison est
négative , la progression est alternée .
; On remarque que lorsque la raison est
négative , la progression est alternée .
Il est d’usage de ne considérer
comme progressions géométriques que les
suites de nombres « positifs » répondant aux conditions de la
définition.
Remarque : On peut dire qu’une
progression géométrique est une suite de terme tels que chacun d’eux est égal
au précédent multiplié par une quantité constante ,
positive. Cette quantité constante, représentant le quotient de deux termes consécutifs , est la
raison de la progression . Ce quotient constant explique la dénomination de
progressions par quotient que l ‘on donne parfois aux progressions
géométriques.
Lorsqu’ on connaît le premier
terme et la raison d’une progression géométrique , il
est facile de calculer successivement tous les termes : il suffit de
multiplier successivement chaque terme par la raison pour avoir le terme
suivant .
Exemple :
Former une progression géométrique de 5 termes dont le premier
terme soit « 625 » et la
raison « 1,2 »
On obtient successivement :
625 ´ 1,
2 =
750 ; 750 ´ 1, 2
= 900 ; 900 ´ 1 , 2 = 1080 ; 1080 ´ 1,2 =
1296
La progression cherchée est donc : 625 ; 750 ; 900 ;
1080 ; 1296
On peut aisément remarquer que les termes d’une progression géométrique
vont en croissant ou en décroissant à
partir du premier terme à gauche, selon que la raison est un nombre plus grand
que « 1 » ou inférieur à « 1 »
REMARQUE :
Il est intéressant de comparer les formules « u1 + ( n - 1) r
) » et « u1 q n - 1 » qui donnent l’une le nième terme d’une progression arithmétique ,
l’autre le nième d’une
progression géométrique. A l’addition
dans la première correspond une multiplication dans la seconde
. De même la multiplication de la raison par « n -1 » dans la
première est remplacée dans la seconde
par une élévation de la raison à la puissance « n - 1 ».
Théorème : Dans une progression géométrique limitée le produit de deux termes , quelconques équidistants des extrêmes est constant
et est égal au produit des extrêmes.
Soi t la progression
géométrique limitée de raison « q »
dont les termes extrêmes sont « a » et « l »
« a ; q a ; a q² ; a q 3 ;
…………………. ; 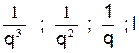 »
»
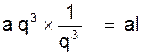
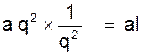
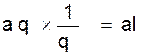
II ) RECHERCHE DU N ème TERME.
Théorème :
Un terme quelconque d’une progression géométriques est
égal au premier terme multiplié par la raison prise autant de fois comme facteur qu’il y a de termes avant lui.
|
Soit la suite géométrique : a ; b ;
c ; d ;….. ;l Avec « a »
étant le premier terme ; Si « q » la raison et
« n » le nombre des termes : Le premier terme est « a » Le second terme est b = a q Le troisième terme est c = b q = (a q)q =
a q2 Le quatrième terme est
d = aq3 La progression peut s’écrire : a ; a q ; a q² ; a q3 ;
a q4 ; ….. ; a qn Donc un terme d’un rang quelconque est égal au premier terme multiplié
par une puissance de la raison ayant un exposant égal au nombre de termes qui
le précèdent. Exemple : la valeur du 5ème terme est égal au 1er « a » multiplié par « q4 ». La
valeur du nème terme est = a q n-1 |
On voit qu’un
terme quelconque est égal au premier multiplié par une puissance de la raison
égale au nombre des termes qui le précèdent ; ainsi le terme de rang
« n » est « a q n-1» :
Exemple 1 : Ainsi le 7ème terme de la progression : 3 ; 6 ; 12 ……..
Dont la raison est « 2 » est égal à : un = 3 ![]() 2 7-1 = 3
2 7-1 = 3 ![]() 2 6
= 3
2 6
= 3 ![]() 64 = 192
64 = 192
Exemple
2 :Calculer le 8e
terme d’une progression géométrique , dont le 1er terme est 4 et la
raison 3
Solution : on applique la
formule : u = a q n-1
u = 4![]() 3 8-1 ; u = 4
3 8-1 ; u = 4![]() 3 7 ; u = 4
3 7 ; u = 4![]() 2 187 ; u = 8 748
2 187 ; u = 8 748
exemple 3 : trouver le 9ème terme de la progression : 2 ; 6 ;
18 ;….
: un
= 2 ![]() 3 8
= 2
3 8
= 2 ![]() 6561 =
13 122
6561 =
13 122
|
FORME
GENERALE : si
l’on désigne « u = un » ;
« a = u1 » dans la formule précédente |
|
Soit
« n » entier supérieur ou
égal à 2 u2=u1 soit u n = u1_ |
|
Formule utilisée en mathématiques
commerciales : Remarque : il arrive parfois que le
premier terme soit appelé u0 u1=u0 u2=u1 u3=u2 un= u0_ |
III )
MOYENNE GEOMETRIQUE :
( info plus sur le calcul des moyennes)
Théorème : dans toute progression géométrique, un terme quelconque
est égal à la « moyenne géométrique » (racine carrée du produit) des
deux termes qui le comprennent.
Si « b » ; « c » ; « d » sont
trois termes consécutifs d’une progression dont la raison est « q » , on a :
« c
= b ´ q » ; « c = d ´ ![]() » ; d’ où
« c² = bd » et « c =
» ; d’ où
« c² = bd » et « c = ![]() »
»
Exemple ► les nombres 1 ; 2 ; 4 ; 8 ;
16 ; 32 ; 64 ;.. forment une progression géométrique de raison
« 2 ».
Vérifions si « 16 » est
égal à la moyenne géométrique de 8 et
32 :
·
. On pose : b = 8
; c =
16 ( 8
fois 2 ) ; d
= 32 ( 16 fois 2) ;
·
Calcul de la valeur de « c » : c
= 8 fois 2 = 16
et c = 32 / 2 = 16
·
. Calcul de c² :
c ²
= 16 fois 16 ou
b fois d = 8 fois 32 ;
c² = 252 ;
d’où ![]() ; c = 16
; c = 16
exercice : soit 3 nombres consécutifs d ‘une suite géométrique : 9 ; x ; 81 ;
déterminez par le calcul la valeur de « x » : puis
déterminez la valeur de la raison « q » .
( racine de 729 ; q = 3 )
|
|
Problème :
Trouver la moyenne géométrique entre deux quantités. |
|
|
Pour obtenir la moyenne géométrique entre deux quantité données on extrait la racine carrée du produit de
ces quantités. Car la proportion continue
|
|
|
|
|
Rappel : En géométrie , on établit qu’un rectangle de largeur
« a » et de longueur « b » est équivalent en surface à un
carré ayant pour côté « x = Par généralisation , on
appelle « moyenne géométrique » entre « n » quantités
« a ; b ; c ; d ; e ; … » une quantité
« x » |
IV ) RECHERCHE DE LA SOMME DES TERMES d’une progression
géométrique limitée.
Résolvons d’abord ce problème pour une progression numérique :
2 ; 6 ; 18 ;
54 ; 162 ; 486
dont la raison est « 3 » , les termes
extrêmes étant « 2 » et « 486 »
la somme des termes est :
S =
2 + 6 + 18 +
54 + 162
+ 486 (1)
Multiplions par la raison « 3 » les deux membres de cette égalité nous avons :
3 S = ( 2 ´ 3) + ( 6 ´ 3) + ( 18 ´ 3) + ( 54 ´ 3) +( 162 ´ 3) +( 486 ´ 3)
(2)
Retranchons membre à membre ( 1) et (2) et
simplifions : il vient :
2 S = ( 486 ´ 3) - 2 ;
on remarque que : « 486 » est le dernier
terme ; « 3 » est la raison ; « 2 » le premier
terme
|
|
d’
où |
; le « 2 » en diviseur représente
la valeur de la raison diminuée de « 1 ». |
GENERALISATION : Soit
la progression géométrique :
« a ; q a ; a q² ; a q 3 ;
…………………. ; 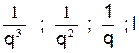 »
»
dont la raison est « q », les
termes extrêmes étant « a » et « l »
la somme de ses termes est :
« S = a + q a +
a q² + a q 3 ; …………………. ;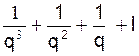 » (1)
» (1)
Multiplions par la raison « q » les deux membres de cette
égalité :
« S q = a q + + a q² + a q 3 +
a q4 ; …………………. ;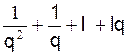 » ( 2)
» ( 2)
retranchons membre à membre
(1) et (2) et simplifions.
S q - S =
l q - a ;
S ( q - 1 ) = l q - a
D’où :
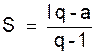
Dans cette formule remplaçons le nième terme « l »
par sa valeur « a qn-1 »
nous obtenons :
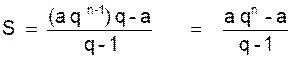
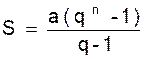
Exemple :
calculer la somme des dix premières puissances de « 2 »
S =
2 + 2 ² + 2 3 +
……………….+ 2 10
Nous appliquons la formule précédente : 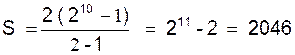
Théorème :
la somme des termes d’une progression géométrique croissante est égale au
produit du dernier terme par la raison , moins 1 , divisée par la raison
diminuée de l’unité.
|
Soit la progression géométrique croissante : a ; b ; c ; d ;
… ; g ; h ; k ; l ; de raison « q » . La somme des termes est : égalité (1)
S = a + b + c + d ……+ g + h + k + l En multipliant par « q » les deux membres de cette égalité,
on trouve égalité ( 2 ) S q = a q + b q + c q + d q
……+ g q + h q+ k q + l q Retranchons ces deux égalités membre à membre en remarquant que a q = b ;
b q = c ; c q = d ; h q = k ; k q = l S q - S =
a q + b q + c q + d q ……+ g q + h q+ k q + l q - a - b - c - d
……- g - h - k - l Et a q - b = 0 ; b q - c = 0 ; c q - d = 0 ………
S q – S = l q - a S (q –1
) = l q - a Donc :
|
|
Exemple 1 : calculer la somme des termes de la progression : 2 ; 6 ;
18 ; 54 ; 162 ; 486 ; 1 458 Remarque : dans une formule précédente on a vu que : « l = a q n - 1 » on
peut alors remplacer « l »
par la valeur donnée dans la première formule. On a alors :
cette formule évite le calcul de « l » Exemple 2 : Calculer la somme des 10 premiers nombres de la
progression : 5 ; 20 ; 80 ;
320 ; ……….
|
|
Solution : |
|
|
Sessa , philosophe indien,
inventa le jeu d’échecs. Son roi , émerveillé de l’attrait de ce jeu savant
et ingénieux, promit à l’inventeur de lui accorder la récompense qu’il
pourrait souhaiter. Le philosophe demanda seulement le nombre de grains de blé qu’on
obtiendrait en mettent un grain sur la 1re case de son échiquier ,
2 sur la deuxième case ; 4 sur la troisième et ainsi de suite en
doublant toujours jusqu'à la 64e . Cette demande sembla ridicule au roi ; combien demandait-il de
grains ? |
Nous appliquons la formule : Ainsi :S = |
|
Réponse : 18 446
744 073 709
551 615 grains |
|
Commentaire : 1 hectolitre ( |
|
EXERXCICES Résolus : |
|
|
1 °) Soit
« u » la suite géométrique de premier terme 2 et de raison 3 Calculer u1 ; u 2 ; u3 ; u9 |
u1 =2 u 2 =6 u3 =18 u9 = 13 122 |
|
2 ° )
Soit « u » la suite géométrique de raison 2 et telle
que u 10 = 2560 Calculer u1 et u 5 |
u 10 = u1
u1 = u5 = u1 |
|
3°) Soit la suite géométrique telle que u10 = 98
415 et u 8 = 10 935 Sachant que u1 est strictement positif, calculer la raison
« q » puis u1. |
u10 = u1 u 8 = u1 donc : soit q2 = d’où
q = 3 ou q = -3 Puisque
u1 et u10 sont positifs ,
« q » est donc positif. Conclusion : q = 3 ; u1 = 5 |
|
On place un capital de 5000
francs à un taux de 5%. Au bout de combien d’années la valeur acquise
sera-t-elle égale au double du capital ? |
u0 = 5000 u1 = 5000 u2 = 5000 un = 5000
on cherche « n » , entier tel que
1,05 n =2 Avec la calculatrice (par essais) , on
constate que 1,0514 =1,98
et que 1,05 15 = 2,08 Au bout de 15 ans , la valeur acquise sera
égale au double du capital. |
Insérer « n » moyens géométriques
Insérer « n » moyens géométriques entre les deux membres
donnés « a » et « b » , c’est à
dire former une progression géométrique de ( n + 2) termes dont « a » et « b »
seront les extrêmes.
TRAVAUX AUTO FORMATIFS.
1) Donner une définition d’une suite
géométrique :
2 ) Qu’appelle t on « raison » dans une suite
géométrique ?:
3 ) Quand dit-on qu’une progression est « croissante ou «
décroissante » ?
4 ) Quelle est la formule qui
permet de trouver (ou d’en déduire) le terme suivant dans une progression
géométrique?
5 ) Quelle est la Formule utilisée en mathématiques
commerciales : qui permet de trouver (ou d’en déduire) le terme suivant
dans une progression géométrique?
EVALUATION
1°) Les progressions suivantes
sont géométriques :calculer la raison « q » :
a)
3 ; 6 ; 12 ; 24 ; …… ( q = 2)
b)
3600 ; 360 ; 36 ; 3,6 ; 0,36 ; …… ( q = 0,1)
c)
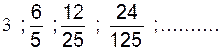 ( )
( )
2°) Dire si les progressions suivantes sont décroissante ou croissante
et pourquoi.
|
|
3 ; 6 ; 12 ;
24 ; 48 Progression
croissante : La raison est 2 En effet : 3 Elle se lit : 3 est à 6 ;comme 6 est à 12 ; comme 12 est à 24 |
|
|
243 ; 81 ; 27 ; 9 ; 3 ; 1 Progression décroissante :est une progression décroissante , dont la raison est Elle se lit : 243 est à 81 ;comme 81 est à 27 ; comme 27 est à 9 |
|
|
2 ; 6 ; 18 ; 54 ; 162 croissante
de raison « 3 » |
|
|
132 ; 66 ; 33 ; 16,5 ; 8,25 décroissante de
raison 1/2 |
|
EXERXCICES
Série 2 |
|
|
1 °) Soit
« u » la suite géométrique de premier terme 2 et de raison 3. Calculer u1 ;
u 2 ; u3 ; u9 |
|
|
2 ° )
Soit « u » la suite géométrique de raison 2 et telle
que u 10 = 2560 Calculer u1 et u 5 |
|
|
3°) Soit la suite géométrique telle que u10 = 98
415 et u 8 = 10 935 Sachant que u1 est strictement positif, calculer la raison
« q » puis u1. |
|
|
On place un capital de 5000
euros à un taux de 5%. Au bout de combien d’années la valeur acquise
sera-t-elle égale au double du capital ? |
|
INTERDISCIPLINARITE
PROBLEMES
|
PROBLEME
1 : |
Solution : |
|
Sessa , philosophe indien,
inventa le jeu d’échecs. Son roi , émerveillé de l’attrait de ce jeu
savant et ingénieux, promit à l’inventeur de lui accorder la récompense qu’il
pourrait souhaiter. Le philosophe demanda seulement le nombre de grains de blé qu’on
obtiendrait en mettent un grain sur la 1re case de son échiquier ,
2 sur la deuxième case ; 4 sur la troisième et ainsi de suite en
doublant toujours jusqu'à la 64e . Cette demande sembla ridicule au roi ; combien demandait-il de
grains ? |
|
|
Réponse : |
|
PROBLEME 2 On donne : en 1998 il y a en France 60 000 000 de personnes . En quelle année la
population aura-t-elle doublée (120 000 000 de personnes )
sachant que sa croissance annuelle est de
3% |
|
SUITE géométrique et intérêts composés :
|
|
PROBLEME 3
Un capital de 9
000 Euros a produit
, capital et intérêts composés , une somme de 12 000 euros , le taux
étant de 5 %. Combien d’année est-il placé ? |
|
PAGE d’exercices supplémentaires :
N°1 : Le 10ème terme d’une progression géométrique est
« 1536 » , la raison est
« 2 » ; trouver le premier terme.
N°2 : Calculer la somme des 10 premiers termes des progressions
suivantes :
a)
1 ; 2 ; 2² ; ……
b)
c)
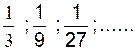
d)
e)
2 ; - 4 ; 8 ; - 16 ; …….
N° 3 : trouver la fraction ordinaire génératrice de la fraction
périodique « 0, 363636…. » considérée comme
la limite de la somme des termes d’une progression géométrique décroissante
illimitée.