|
|
|
|
Les suites géométriques |
|
|
|
|
|
Les puissances de dix |
|
ENVIRONNEMENT du dossier:
|
Objectif précédent : |
3°) la représentation graphique et l’échelle
logarithmique. 4°)
les logarithmes vulgaires n°2 |
|
DOSSIER : Les « Suites » logarithmiques
vulgaires (n°1)
1.
Avantages des logarithmes.
2.
Définition.
3.
logarithmes décimaux : appelé système des logarithmes vulgaires ou, Système base 10 ou encore appelé logarithmes de Briggs.
|
TEST |
COURS |
Devoir évaluation |
Interdisciplinarité
|
|
Corrigé Contrôle |
Corrigé évaluation
|
Définition.
Considérons deux progressions croissantes , l’une arithmétique commençant par zéro ,
l’autre géométrique commençant par 1 ; si l’on désigne par « r »
la raison de la progression arithmétique et par « q » la raison de la
progression géométrique , ces deux progressions peuvent s’écrire :
0 ; r ; 2r ; 3r ; 4r ; 5r ;
…………nr
1 ; q1 ; q2 ;
q3 ; q4 ; q5 ; ……… ;qn ;
On dit que chaque terme de la
progression arithmétique est le logarithme du terme de même rang de la
progression géométrique.
Ainsi :
3r est
le logarithme de q3
4r est
le logarithme de q4
5r est
le logarithme de q5
nr est le logarithme de qn
L’ensemble des deux progressions constitue un système de logarithme . La seule condition à réaliser pour constituer
un système de logarithmes est que la progression arithmétique commence par zéro
et que la progression géométrique commence par l’unité ; on en tire les
remarques suivantes :
Remarques 1 : il existe une
infinité de systèmes de logarithmes puisque la raison de chacune des progression est arbitraire.
Soit le système suivant (base 2)
0 ; 1 ;2 ;3 ;4 ; 5 ;.…
1 ; 2 ; 22 ;23 ;24 ;25 ;
…..
le
logarithme de 23 ou 8 est 3
Soit un autre système suivant (base 2)
0 ; 3 ;
6 ; 9 ; 12 ; 15 ;.…
1 ; 2 ; 22 ; 23 ;24 ;25 ; …..
le
logarithme de 23 ou 8 est 9
Remarquons que les opérations sur les nombres , si on les ramène aux opérations sur les
logarithmes , sont ramenées à des
opérations d’ordre moins élevé :
Une multiplication est remplacée par
une addition ;
Une élévation à une puissance est
remplacée par une multiplication ;
Une division est remplacée par une
soustraction : Une extraction de racine est remplacée par une division.
S’il était possible d’obtenir
rapidement le logarithme d’un nombre donné , et
inversement d’obtenir le nombre dont le logarithme est donné , toutes les
opérations seraient diminuées de difficulté grâce aux logarithmes .
Les tables de logarithmes remplissent
ce rôle , lorsque l’on connaît les règles permettant
de les utiliser .
Rappels :les « Suites
géométriques »
Nous
ne considérons ici que les raisons positives.
1°) La suite 2 ; 6 ; 18
, 54 ; 162 , où chaque
nombre s’obtient en multipliant le
précédent par (+3) constitue une
progression géométrique de raison « 3 »
2°) La suite a ,
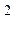aq , aq
; aq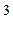
,…..est une progression géométrique de raison « q »
.
Si
« q » est supérieur à 1 , la progression est
dite « croissante ».
Exemple :
pour « q » = 2 et a=5 ;nous obtenons : 5 ; 10 ; 20 ;
40 ; 80 ;…
Si
« q » est inférieur à 1 , la progression est
dite « décroissante ».
Exemple : pour
« q » = 
et a= 2
Nous
obtenons le début de la suite : 2 , 0,2 ; 0,02 ; 0 , 002 ;…
En
résumé : une suite « géométrique » est une suite de nombres tels
que chacun d’eux s’obtient en multipliant le précédent par un nombre constant appelé
« raison »
Système base
10 : appelé système des logarithmes vulgaires ou logarithmes décimaux , ou encore appelé logarithmes de Briggs
L’invention
des logarithmes est due à Neper , baron écossais (
1550 – 1617) . Briggs , son contemporain et ami professeur
de mathématiques à Londres , publia en 1624 les premières tables de logarithmes
vulgaires.
Remarque 2 : On appelle « base » d’un système de
logarithmes le nombre dont le logarithme est égal à l’unité .
Ainsi
, dans le premier système que nous avons écrit , la base est
« 2 » , dans le système des logarithmes vulgaires ou décimaux , la
base est 10.
On peut remarquer que
, par définition , le logarithme de 1 est dans tous les systèmes égal à
zéro.
Remarque 3 :
propriété remarquable des logarithmes
La considération du système général de
logarithmes :
0 ; r ; 2r ; 3r ; 4r ; 5r ;
…………nr
1 ; q1 ; q2 ;
q3 ; q4 ; q5 ; ……… ;qn ;
nous permet d’énoncer cette propriété
remarquable : Chaque terme de la progression géométrique a pour logarithme
un nombre égal au produit de son exposant par la raison de la progression arithmétique .
On écrit : log qn = nr
Ce qui s’énonce logarithme de qn égale
nr
Cette remarque est importante elle permettra d’établir aisément les
propriétés essentielles des logarithmes .
Définition : « Logarithmes
décimaux »
Explication :
Ecrivons
l’une au –dessous de l’autre :
1°) une progression géométrique ayant
un terme égal à 1 est pour raison 10 ;
2°)pour une
progression arithmétique ayant un terme égal à 0 et pour raison 1 , en faisant
correspondre au terme 1 de la première le terme 0 de la seconde :
|
|
…… |
0 ,001 |
0,01 |
0,1 |
1 |
10 |
100 |
1000 |
…(1) |
|
Prog.
arithmétique |
|
- 3 |
- 2 |
-1 |
0 |
1 |
2 |
3 |
..(2 ) |
Tout nombre de la deuxième ligne est
appelé le « logarithme décimale » du nombre correspondant de la
première ligne
Ainsi on écrira que (par
exemples)
Log 100 = 2
Log
0,1 = -1
« Le
logarithme décimal de 100 est égal à 2 »
« Le
logarithme décimal de 0,1 est égal à -1 »
Imaginons qu’entre deux nombres
consécutifs de la 1er ligne et entre les deux nombres correspondants
de la deuxième ligne ,
on insère deux progression formées du
même nombre de termes :
|
Progr. géométrique |
…… |
10 |
a |
b |
c |
d |
100 |
….. |
e |
|
Prog. arithmétique |
|
1 |
a’ |
b’ |
c’ |
d’ |
2 |
|
|
Le terme « a’ » de la
deuxième ligne est le logarithme décimal du terme correspondant « a »
de la première ligne :
On écrira : log a = a’
Examen
des résultats précédents :
De l’examen des progressions (1 )
et (2 ) il résulte que :
1°) les nombres négatifs n’ont pas de
logarithmes.
2°)le
logarithme de 1 est égal à 0
3°) les logarithmes des nombres
positifs plus grand que 1 sont positifs.
4°)les logarithmes
des nombres positifs plus petits que 1 sont négatifs ;
5°)seules
les puissances de 10 ont pour
logarithmes des nombres entiers :
log 1000 = 3 ; log 0,0001 = - 4
PROPRIETES des logarithmes.
Nous allons établir les propriétés des logarithmes
en utilisant les logarithmes des puissances de dix ,
mais ces propriétés s’appliquent aux logarithmes de tous les nombres.
Théorème 1 : Le logarithme d’un produit de facteurs est égal à la somme des
logarithmes des facteurs.
Considérons le produit de 10 par 10
, qui s’obtient en additionnant les exposants des facteurs. 
Il en résulte de la définition des logarithmes que :
Log
= 5
Log 
= 3
Log 
= 2
Or : 5 =3 + 2
Donc
on peut écrire : Log = Log + Log
Si nous généralisons : log ( a 
bc ) = log a + log b + log c
Théorème 2 : le logarithme d’un quotient est égal
au logarithme d’un quotient est égal au logarithme du dividende moins le logarithme du diviseur.
Soit le quotient : = q on sait que D = d q
Appliquons le théorème précédent
log D = log d + log q
On transforme : log q
= log D – log d
On peut donc écrire que : log 
= log D – log d
Théorème 3 : Le logarithme d’une puissance d’un nombre est égal au produit du logarithme de ce
nombre par l’exposant de la puissance.
a
= a
aaaa
appliquons le
théorème relatif au produit des facteurs :
log a = log
a + log a + log a + log a + log a
soit (factorisons le deuxième membre)
log a = 5 log
a
on peut
donc généraliser : log a
= n log a
Théorème
4 : le logarithme d’une racine
d’un nombre est
égal au quotient du logarithme de
ce nombre divisé par l’indice de la racine .
Soit 
= b
D’après la définition de la racine « quatrième » d’un nombre , cette
égalité est équivalente à : a
= 
ou à
l’ égalité équivalente : 
= b
1 ° ) Appliquons
le théorème précédent pour :
a =
log a = 4 log b
log b = 
log a
log = log a
2 ° )
Appliquons le théorème précédent pour : = b
log = log a
|
|
en généralisant : log |
|
TRAVAUX AUTO - FORMATIFS
Compléter les phrases suivantes :
1°)
les nombres négatifs n’ont pas ………………………………..
2°)le logarithme de 1 est égal à ……………………………………..
3°)
les logarithmes des nombres positifs plus grand que 1 ……………………………….
4°)les logarithmes des nombres positifs plus petits que 1 ……………………………….. ;
5°)seules les
puissances de 10 ont pour logarithmes
des nombres ………………..
exemple :
log 1000 =
PROPRIETES des logarithmes.
Théorème
1 :
Le
logarithme d’un produit de facteurs est
égal ……………………………………………….
Si
nous généralisons : log ( a bc ) = ……………………………………………………….
Théorème 2 : le logarithme d’un quotient est égal
……………………………………………
On
peut donc écrire que : log =
Théorème
3 :
Le
logarithme d’une puissance
d’un nombre est égal ………………………………………...
on peut donc
généraliser : log a = ?
Théorème
4 : le logarithme d’une racine d’un nombre est égal …………………………….
|
|
|
|
EVALUATION
Le
logarithme décimal de 2 est 0 , 30103
.
1°)
quels sont les logarithmes de 4 ;
5 ; 8 ; 16 , ; 20 ; 32 ;
40 ; 50 ?
2°)
quels sont les logarithmes de 0,02 ; 0,2 ; 20 ; 200 ; 2
000 ?
3°)quels sont les logarithmes de 0,1 ; 0,2 ;
0,4 ; 0,5 ; 0,8 ?
A
l’aide des résultats de l’exercice précédent , tracez la courbe qui représente la fonction y =
log x pour les valeurs e « x »
comprises entre 0,01 ; et 10.
Echelle
des abscisses :
Echelle
des ordonnées :
Quelle
est la racine carrée de 8 ?
Quel
est le logarithme de cette racine ?
Quelle
est la racine carrée de 10 ?
Quel est sont logarithme ?
Déduire
une valeur approchée du logarithme de « 3 » ; puis une valeur
approchée des logarithmes de 6 ; 9 ; 12 ; 15 .
Calculer
les nombres dont les logarithmes sont 0, 25 ; 1 ,25 ; 2 ; 25 .
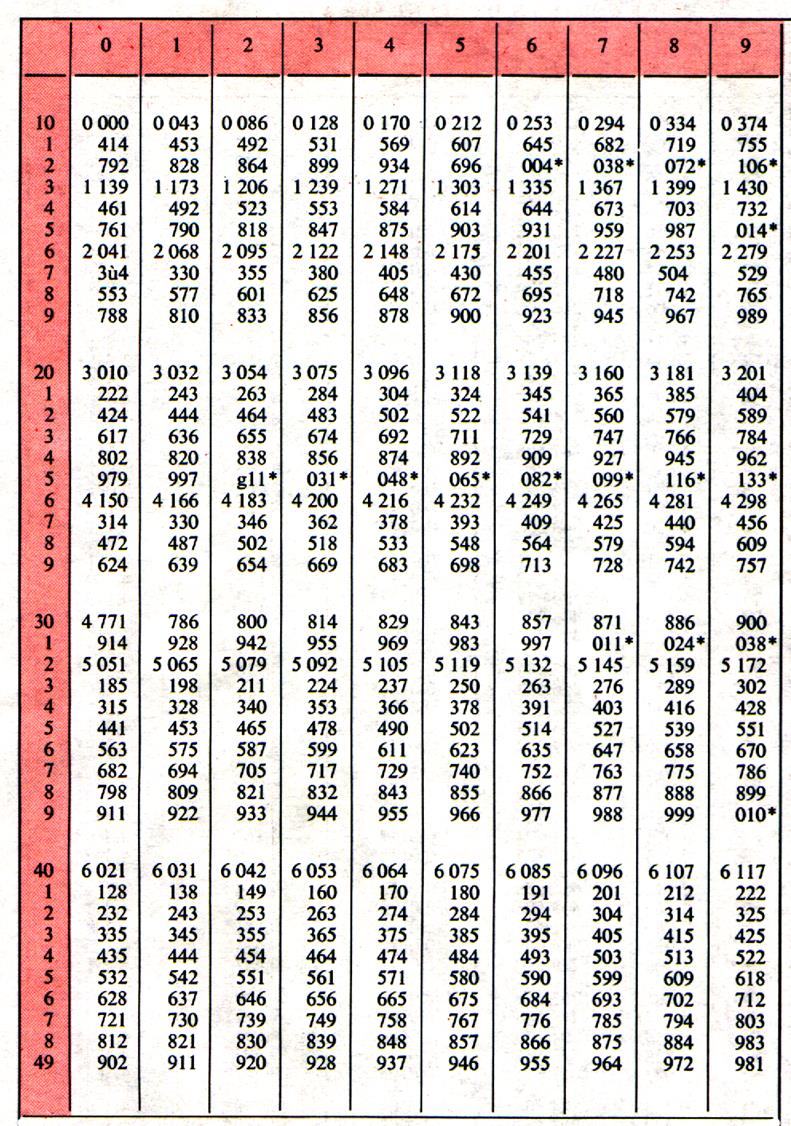
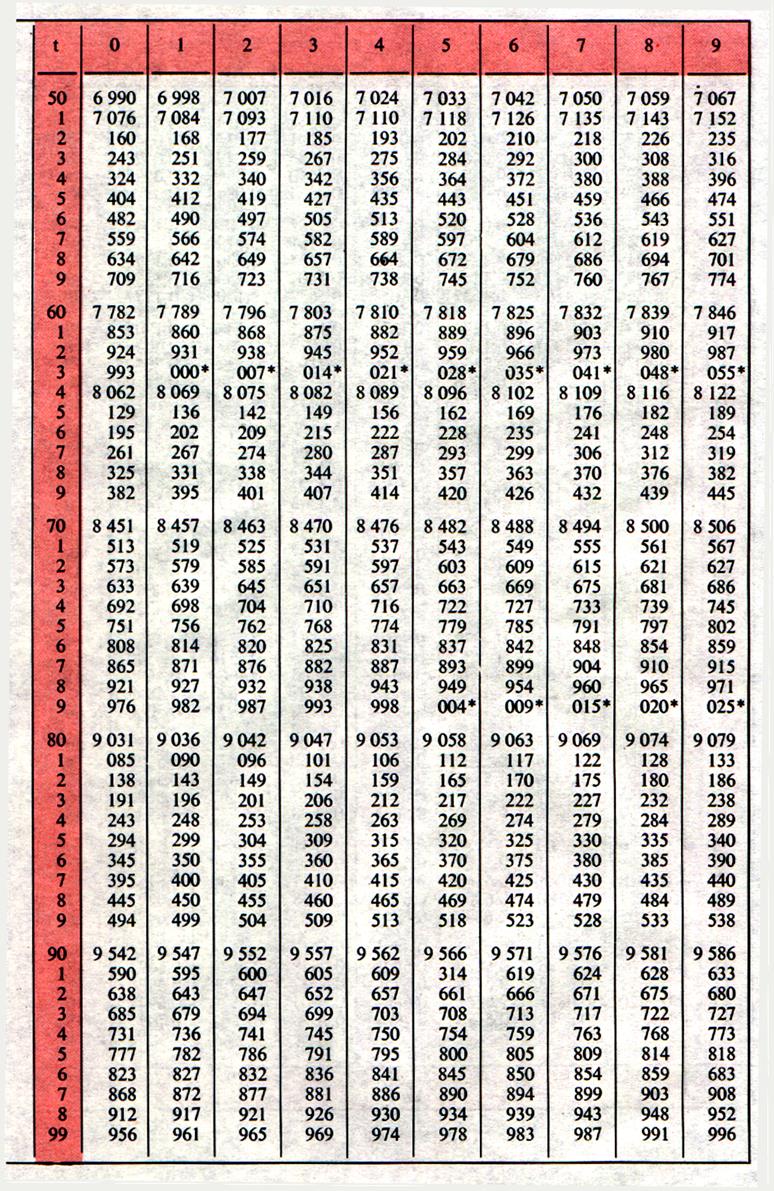
Utilisation
de la calculatrice :
Prendre
des nombres entre 0 et 1000 ; Chercher leur logarithme
et comparer votre résultat avec la table ci jointe.
Physique :
|
Les
logarithmes décimaux des nombres entiers ( N ) de 0 à 1000 . feuille
2/2 |
|
|
CORRIGE
- CONTROLE :
Compléter les phrases suivantes :
1°)
les nombres négatifs n’ont pas de logarithmes.
2°)le
logarithme de 1 est égal à 0
3°) les
logarithmes des nombres positifs plus grand que 1 sont positifs.
4°)les
logarithmes des nombres positifs plus petits que 1 sont négatifs ;
5°)seules
les puissances de 10 ont pour
logarithmes des nombres entiers :
exemple : log 1000
= 3 ; log 0,0001 = - 4
PROPRIETES des logarithmes.
Théorème
1 :
Le
logarithme d’un produit de facteurs est
égal à la somme des logarithmes des facteurs.
Si
nous généralisons : log ( a bc ) = log a + log b + log c
Théorème 2 : le logarithme d’un quotient est égal
au logarithme du dividende moins le
logarithme du diviseur.
On
peut donc écrire que : log = log D – log d
Théorème
3 :
Le
logarithme d’une puissance
d’un nombre est égal au produit du logarithme de ce nombre par
l’exposant de la puissance.
on peut donc
généraliser : log a = n log a
Théorème
4 : le logarithme d’une racine d’un nombre est égal au quotient du logarithme de ce nombre par l’indice de la racine .
|
|
en généralisant : log |
|