la fonction logarithmique ((résumé)

Pré requis:

Les fonctions. (pré requis )
Les fonctions généralités
Les logarithmes (1) ; les logarithmes (2)

ENVIRONNEMENT du dossier:

	Objectif précédent	Objectif suivant
Index warmaths	la fonction homographique	1°) Les logarithmes népériens et décimales	Liste des cours sur les fonctions.
	Les suites logarithmiques	2°) La fonction exponentielle	Liste des cours disponibles sur les logarithmes.
		3°) >>> cliquer ici : COURS n°2 :

DOSSIER : LA FONCTION LOGARITHME « népérien »

1 ) Résumé :
	· Définition
	Représentation graphique de la fonction : log x
	Relations fondamentales.
	Exercices : Résoudre .

		Travaux auto formatifs			Corrigé des Travaux auto formatifs
TEST		Devoir Contrôle	Devoir évaluation	Interdisciplinarité :	Corrigé Contrôle	Corrigé évaluation
	Corriger des travaux.

RESUME DU COURS :

	Définition : On désigne log x ou ln x (lire logarithme népérien de x ) la primitive de ( x > 0 ) qui s’annule pour x = 1 Ainsi y = log x Þ y ‘ =
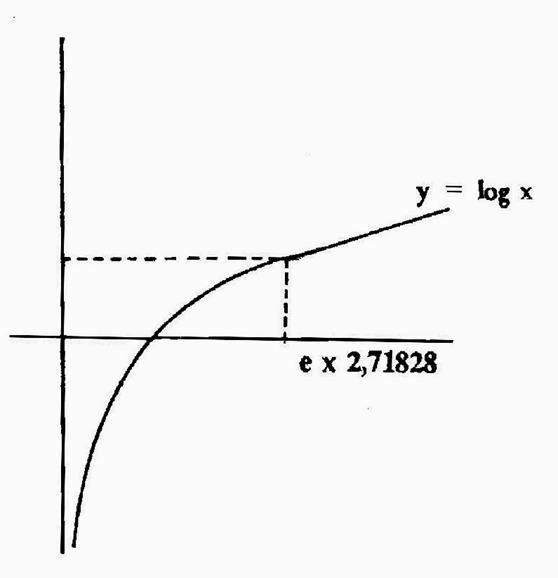
	Représentation graphique de la fonction : log x
		Domaine de définition : (Df) Df = ] 0 ; + [ Lim. log x = - x 0 ⁺ Lim. log x = + x +
	Relations fondamentales.	Exemple :
	Log a b = log a + log b	Résoudre : Log x + log 6 = 2 log 4
	Log = log a - log b	Log 6 x = log 4 ²
	Log = log 1 - log c = 0 - log c = - log c	6 x = 16
	Log a ⁿ = n log a	x =

TRAVAUX AUTO FORMATIFS.

	CONTRÔLE :

	Traduire : log x ou ln x
	Quelle est la forme de la représentation graphique de log x
	Compléter l’égalité :
	Log a b =
	Log =
	Log =
	Log a ⁿ =

	EVALUATION :

	Exercices : Résoudre .

1.	Log x + log 6 = 2 log 4
2.	2 log x + log 8 = 2 log x
3.	2 log x + log 8 = 2 log 4
4.	- log x + 2 log x = 2 log x
5.	log 2 x = log 2 + log 4
6.	log ( x + 1 ) + log ( x + 5 ) = log 96
7.	Log 2 x + log x + 2 = log 8