|
Les suites géométriques |
|
|
Les suites
arithmétiques |
|
|
Les puissances de dix |
ENVIRONNEMENT du dossier:
|
Objectif
précédent : |
Objectif suivant : Application 1 :
Etude simple de la fonction exponentielle et des logarithmes |
DOSSIER
n° 1 : Les
logarithmiques vulgaires
|
TEST |
COURS |
Interdisciplinarité |
|
CHAPITRES :
|
I ) Idée de logarithmes . |
|
|
II) Trouver le logarithme d’un nombre donné . |
|
|
III ) Trouver le nombre correspondant à un
logarithme donné. |
|
|
Recherche d’un produit par les
logarithmes |
|
|
Recherche d’un
quotient par les logarithmes |
|
|
Recherche d’une
puissance par les logarithmes |
|
|
Recherche d’une
racine par les logarithmes |
|
|
Calcul , par
les logarithmes, d’une expression numérique |
|
|
Exercices
spéciaux sur les logarithmes |
|
I ) Idée de logarithmes .
Soient les deux progressions
ci dessous , la première géométrique , la deuxième arithmétique :
|
|
0,001 |
0,01 |
0,1 |
1 |
10 |
100 |
1000 |
10
000 |
Etc. |
|
|
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
Etc. |
1er exemple : « multiplication »
II) Soit effectuer :
10![]() 1000
1000
Cherchons dans la deuxième
progression les nombres qui correspondent aux nombres 10 et 1000 . On
trouve 1 et 3 . Additionnons , on obtient 4 . Cherchons 4 dans la première progression et relevons le
nombre correspondant dans la première progression . On trouve 10 000 . Le
produit demandé est 10 000 .
Les nombres 1 ; 3 ; 4 et tous les termes de la
deuxième progression sont appelés les logarithmes des nombres correspondant de
la première progression .
On dira : log. 10 = 1
log . 1 000 = 3
log
10 000 = 4
On voit que pour effectuer une multiplication , il a suffit de faire une
addition de logarithmes et de chercher le nombre correspondant au total .
Conséquence – le logarithme
d’un produit est égal à la somme des logarithmes des facteurs . (
facteur 10 et facteur 1000)
2ème exemple :
« division »
Soit effectuer : 10
000 : 100
Cherchons dans la deuxième
progression les logarithmes de 10 000 et de 100
On a : log 10000 = 4
log. 100 = 2
Soustrayons les deux logarithmes , on obtient 2 . Cherchons le nombre qui correspond au
logarithme 2 , c’est 100 . Le quotient cherché
est 100 .
On voit que pour effectuer
une division de deux nombres , il suffit
de faire la soustraction des logarithmes de ces nombres et de chercher le
nombre correspondant au logarithme de la différence .
Conséquence : le
logarithme d’un quotient est égal au logarithme du dividende moins le
logarithme du diviseur .
log.
(![]() ) = log. 10000-
log 100
) = log. 10000-
log 100
3ème Exemple
« puissance »
Soit à effectuer 10 3
On cherche dans la deuxième
progression le logarithme de 10 , que l’on multiplie par l’exposant 3 . On
obtient 1![]() 3 ou 3 .
3 ou 3 .
A ce logarithme , correspond le nombre 1 000 , qui est la
puissance cherchée .
On voit que pour effectuer
la puissance d’un nombre , il suffit de multiplier le logarithme de ce nombre
par l’exposant et de chercher ensuite le
nombre correspondant au produit trouvé .
Conséquence : le
logarithme d’une puissance d’un nombre est égal au logarithme de ce nombre
multiplié par l’exposant de la puissance.
4ème exemple « puissance »
Soit à effectuer ![]()
On cherche dans la deuxième
progression le logarithme de 100 , c’est 2 . On divise ce logarithme par
l’indice de la racine , qui est ici 2 . On obtient 1 . Il suffit de
relever le nombre correspondant au logarithme 1 . C’est 10 , qui est la racine
cherchée .
On voit que pour effectuer
la racine d’un nombre , il suffit de diviser le logarithme de ce nombre par
l’indice de la racine et de chercher ensuite le nombre correspondant au quotient trouvé .
Conséquence . Le logarithme
d’une racine d’un nombre est égal au logarithme
de ce nombre divisé par l’indice de la racine .
Tables de logarithmes
. Des savants ont dressé ce qu’on a
appelé des tables de logarithmes ;c’est à dire qu’ils ont calculé les
termes de progressions géométriques , correspondant à des termes de progressions arithmétiques .
Les calculs sont tous faits . Il suffit de relever les
résultats . Des exercices montreront mieux que toute théorie comment on doit se
servir de ces tables .
EXERCICES SUR LES CALCULS DE LOGARITHMES
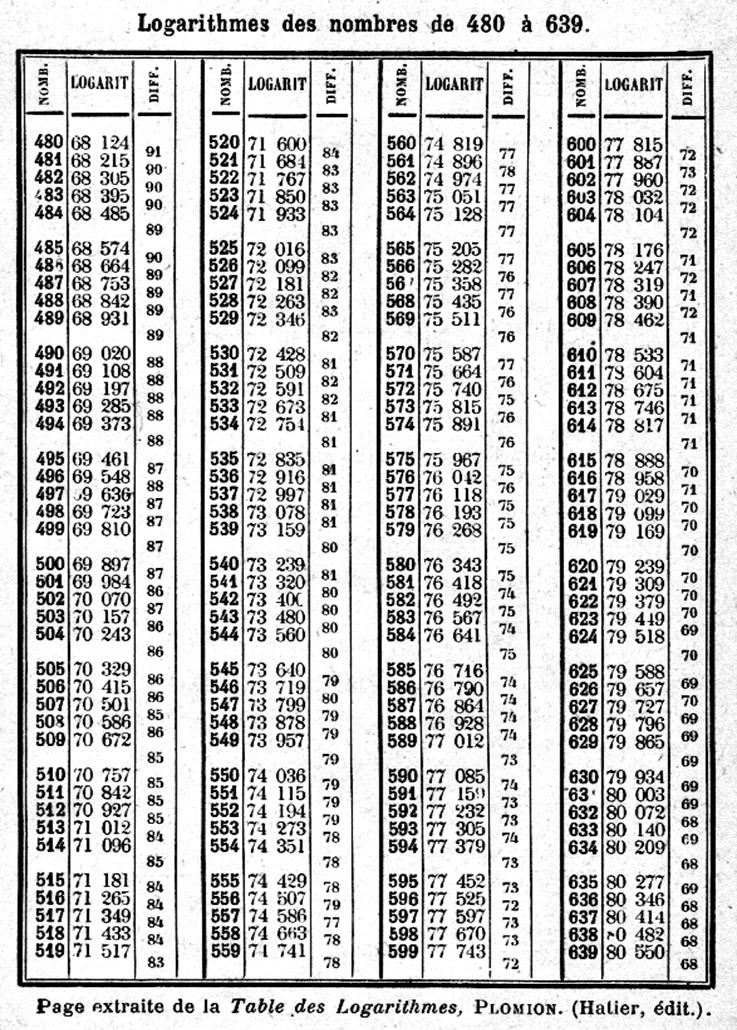
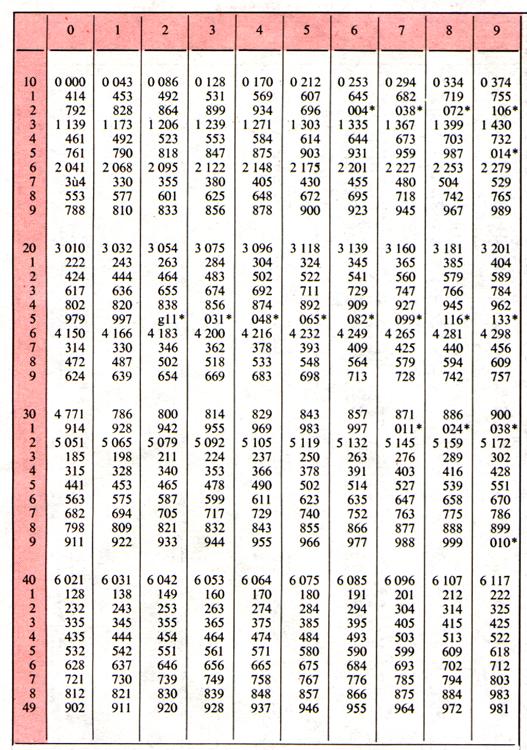
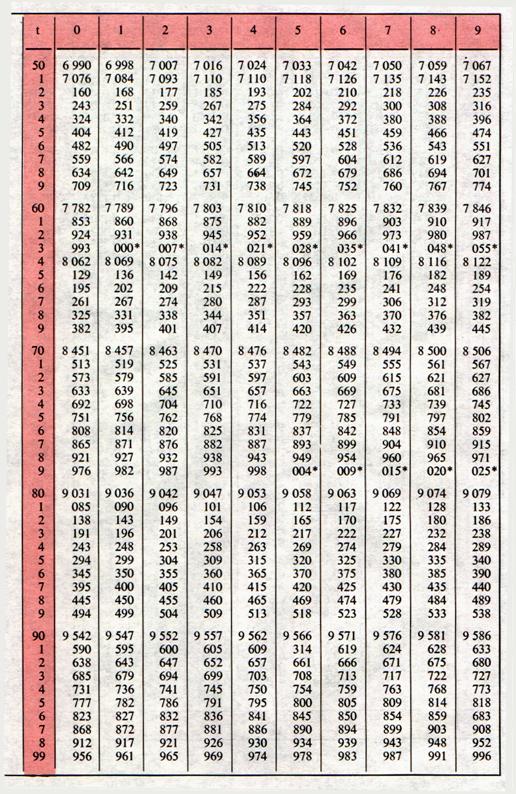
Extrait des tables
|
|
Trouver le logarithme d’un nombre
donné : nombre à trois chiffres
Exercice 1 :
a) Trouver le logarithme du
nombre 493 ,avec une table
On cherche dans l’extrait
de la table , le nombre
« 493 » dans la colonne des nombres , indiquée N . Puis on prend le
logarithme inscrit en face , on trouve
69 285 , ce nombre s’appelle
« mantisse » .
On compte le nombre de
chiffres du nombre « 493 » , c’est « 3 » . On retire 1 à
cette somme et on obtient « 2 » , qui est appelé la
« caractéristique » . On place cette caractéristique devant « 69 285 » , en les séparant par une virgule ; et
on écrit :
Log. 493 =
2 , 69285
b ) Trouver le logarithme du nombre 493 Avec la calculatrice :
taper « 493 » puis
« log » : le résultat affiché est : 2 ,
692846919
Utilité de la
caractéristique :
La caractéristique
« 2 » indique que le nombre dont provient le logarithme est compris
entre 100 et 1000 , c’est à dire à 3 chiffres .
Règle . La caractéristique d’un logarithme est toujours égale au nombre
de chiffres entiers , moins un , du nombre considéré .
Remarque : on peut
tirer de ce qui précède que :
log. de 49,3
= 1 , 69285
log. de 4,93 =
0, 69285
EXERCICE II : Trouver le logarithme du nombre
0,0493 .
On cherche le logarithme du
nombre 493 , c’est toujours comme mantisse
69 285 .Reste à trouver la
caractéristique .
Or , : 0,0493 = ![]() ou log. 493
moins log. 10 000
ou log. 493
moins log. 10 000
Ou 2, 69285
- 4
Pour retrancher 4 de 2 , on inscrira -2 qui
est le résultat , mais en l’indiquant comme ci-dessous :
![]() , 69285
, 69285
d’où log. 0,0493
= ![]() , 69285
, 69285
Remarque .- On voit qu’ainsi tous les logarithmes obtenus
ont leur partie décimales positive , il n’ y a que la caractéristique qui
peut-être négative . Cela facilite les calculs .
Règle : La
caractéristique d’un nombre inférieur à 1 indique le rang du premier chiffre
significatif à droite après la virgule .
NOMBRES
DE 4 CHIFFRES :
Exercice : Trouver le logarithme du nombre 4936
On cherche dans la table le
logarithme de 493 , qui est le même que
celui de 4930 , mais avec la
caractéristique « 3 » .
On a :
log 4 930 = 3 , 69285
Mais ce n’est pas ce
nombre 4 930 dont il faut chercher le
logarithme , c’est 4 936 , c’est à dire
un nombre supérieur de 6 unités .
Pour un nombre supérieur de
10 unités , c’est à dire pour le nombre 4940 , la différence de logarithmes est
de 88 ( colonne des différences) .
On dira : 1à unités correspond
à une différence de logarithme égale à
88 , à quelle différence correspond 6 unités ? La règle de trois suivante
donne :
![]() = 52, 8 ou
53
= 52, 8 ou
53
On ajoute ce nombre 53 au
log. de 4930 , et l’on a
3,69285
+ 0,00053 = 3 , 69338
qui est le logarithme du
nombre 4 936
A l’aide de la calculatrice
le log.
4936 = 3,693375151
NOMBRES DE 5 CHIFFRES
Exercice : Trouver le logarithme du nombre 57 789 .
Cherchons dans la table les
logarithmes de 57 700 et 57 800 ;puisque
57 789 est compris entre 57 700
et 57 800.
On a : log. 57 700
= 4 ,76118
Et
log. 57 800 = 4,76193
Pour une différence de 100
unités entre les 2 nombres , on trouve une différence de 75 entre les
logarithmes ( colonne spéciale)
Comme dans l’exercice
précédent , on fera la règle de trois suivante , en regardant que le nombre
proposé 57 789 surpasse de 89 unités le nombre
57 700 ;
![]() = 67 par excès .
= 67 par excès .
On doit donc ajouter 67 au
log. de 57 700 , c’est à dire à 4,76118
.
On obtient : log. 57 789 = 4, 76185
II TROUVER LE
NOMBRE CORRESPONDANT A UN LOGARITHME DONNE .
Exercice 1
Trouver le nombre
correspondant au logarithme 2,79 934
On ne s’inquiète pas de la
caractéristique , qui indique seulement que le nombre cherché doit avoir 3
chiffres entiers .
On cherche dans la colonne des logarithmes la
mantisse 79 934 qui s’y trouve justement . Elle correspond à
un nombre : 630 . C’est le nombre cherché .
Exercice 2 :
Trouver le nombre
correspondant au logarithme 0, 69679
Ce nombre aura 1
chiffre entier d’après la
caractéristique 0
Cherchons dans les colonnes
des logarithmes , on ne trouve pas 69 679 , qui est compris entre
69 636 , correspondant au nombre 497
et 69 723
, correspondant au nombre 498
et qui est supérieur de 43 unités à 69936
le nombre cherché sera
entre 497 et 498
On dit : Pour une
différence de logarithme de 69723 – 69636 ou 87 (indiquée dans la colonne
des différences ) , on a une différence de nombres égale à 4980 – 4970 ou 10
unités .
Une règle de trois donnera
le quatrième chiffre à ajouter à 497.
Pour une différence de
logarithme de 87 unités , on doit ajouter 10 unités au nombre 4930 , pour une
différence de logarithme de 43 unités , on devra ajouter : ![]() = 5
= 5
Le nombre sera donc :
4,975
La
calculatrice donne pour log. de 0,69679
= 4,974964659
Exercice 3 :
Trouver le nombre
correspondant au logarithme ![]() ,69082
,69082
On cherche 69082 dans les colonnes de logarithmes . (voir page précédente)
On trouve 69020 . Il y a donc une différence de 62 de
plus . Or , la différence tabulaire
correspond à 69020 est de 88.
On posera la règle de trois
suivante , si on veut avoir 5 chiffres du nombre .
Pour 88 : la différence
des nombres 49 000 et 49 100 = 100
Pour « 1 » la différence : ![]()
Pour « 62 » la
différence : ![]() = 70
= 70
Le nombre demandé sera
donc : 49 070 , mais comme la caractéristique est de ![]() , il s’ensuit que le
premier chiffre significatif du nombre 49070 doit venir après la virgule .
, il s’ensuit que le
premier chiffre significatif du nombre 49070 doit venir après la virgule .
Le nombre demandé
est : 0,49070.
RECHERCHE D’UN PRODUIT PAR LES LOGARITHMES.
On a vu que les produits de
facteurs se transforme en additions des logarithmes de ces facteurs .
Exercice 1
Effectuer la
multiplication : 492,7 ![]() 0,51
0,51![]() 517
517
On disposera ainsi :
; log.
492,7 = 2,69258
log.
0,51 = ![]() ,70757
,70757
log.
517 = 2,71349
somme 5,11364 =
nombre 129 910
(voir le résultat avec une calculatrice : 129 910 , 2274 )
Le logarithme 5,11364 est le logarithme du produit .
Recherchons dans une table
complète le nombre correspondant à ce logarithme , et le produit sera effectué .
Dans la table , on a le logarithme 11059 , qui est le plus
approché de 11364 . Il correspond au
nombre 129 ou 129 000 , puisqu’il nous faut ici 6 chiffres entiers à cause de
la caractéristique « 5 » . On dira :
Pour une différence de 335
en logarithme , on aura une différence de 1 000 unités sur un nombre .
Pour une différence de logarithme de
11364 – 11059 ou 305 , on aura une différence de nombre égale à : ![]() = 910
= 910
Le produit sera donc :
1239 910
Le produit est 129910 ,
qu’on retrouve en faisant les
multiplications ordinaires . ( ou avec la calculatrice )
RECHERCHE D’UN QUOTIENT PAR LES LOGARITHMES
On a vu que tout division
de nombres se traduisait par une différence de logarithmes .
Exercice : Effectuer la division 4968,3 : 51,4
On disposera :
log.
4 968,3 = 3 , 69620
log.
51,4 = 1, 71096
Différence : 1, 98524
On recherchera dans la
table , le nombre correspondant au logarithme 1, 98524 et l’on trouvera après
calcul : 96,65
Qui est le quotient demandé
.
RECHERCHE
D’UNE PUISSANCE PAR LES LOGARITHMES
RECHERCHE
D’UNE RACINE PAR LES LOGARITHMES
Compléter les phrases suivantes :
EVALUATION
|
Les logarithmes décimaux des nombres entiers ( N
) de 0 à 1000 . feuille 2/2 |
|
|