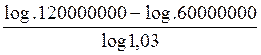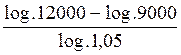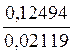Pré requis:

Les suites géométriques
Les suites arithmétiques
Les puissances de dix

ENVIRONNEMENT du dossier:

Index

Objectif précédent : 1°)Les suites géométriques 2°)Les suites arithmétiques

Objectif suivant : 1°) les logarithmes vulgaires

tableau     195 Liste des cours sur le module  :  les logarithmes.

 

Module les log…. : Etude simple  de la   fonction exponentielle et des logarithmes

Problèmes résolus .

 

	Problème  1     :   Problème de la population croissante .
	PROBLEME    2 : On donne : en 1998  il y a en France 60 000 000 de personnes .En quelle année la population aura-t-elle doublée (120 000 000 de personnes ) sachant que sa croissance annuelle est de  3%
	PROBLEME    3 :   Un capital de 9 000   Euros  à produit , capital et intérêts composés , une somme de 12 000  euros , le taux étant de 5 %. Combien d’année est-il placé ?
	Problème     4 : La première année de son ouverture au public , un musée est visité par 250 000 personnes. Durant les années suivantes on enregistre une diminution annuelle de 8 % du nombre de visiteurs………………………………..

 

 

 

TEST

COURS

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

 

 

COURS

 

 

Problème de la population croissante .

 

Imaginons une contrée où les conditions de la vie persistent sans changement . Soit la population initiale  1000  N habitants ( N étant assez grand) Supposons la mortalité persistant à 19 pour mille par an , et la natalité persistant à 20 pour mille :

Question : que deviendra la population , au bout d’un an , de 10 ans , 100 ans , …….? Quand aura t- elle doublée ?

 

Vous direz : la population actuelle est  1 000  ( voulant signifier 1000 N) Elle deviendra 1001au bout de 1 an , augmentant de un millième de sa valeur .

 C’est exacte . Mais n’ajoutez pas qu’elle deviendra 1 002 au bout de 2 ans , 1003 au bout de 3 ans , qu’elle doublera en 1000 ans par progression arithmétique . Ce calcul , à peu prés valable en grossière approximation pour les premières années , devient de plus en plus erroné . Pour bien souligner l’erreur , disons que c’est en 693 ans ( et non pas en 1 000 ans ) que la population doublerait .Ou , sous une autre forme  , disons qu’en  1 000 ans la population ne serait pas seulement doublée mais qu’ elle  deviendrait 2 718 ;elle serait multipliée par 2,718 .

 

Ces deux nombres  693 ( au lieu de 1 000) et  2,718 ( au lieu de 2 ) marquent le même fait : que la population croît en progression géométrique  et non en progression arithmétique , que la fonction est exponentielle .

 

Principe de la solution exacte .

 

La  1^ère année , la population croît du millième de sa valeur 1 000 . Elle devient 1 000 + 1 = 1001 . Elle est multipliée par 1,001.

 

La 2^ème année , elle croît du millième de sa nouvelle valeur 1 001 .

 

Elle devient 1001 +   1001  = 1001 (  1  +  )

 

=1001 (  + )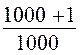

 

= 1001 ()

 

=  1001   1,001

               =  1000 1,001  1,001

 

              Et chaque année , on peut calculer la nouvelle valeur en multipliant la précédente valeur par ce facteur 1,001  raison de la progression géométrique .

 

On a donc :

Population initiale ……………………..1 000

Population au bout de 1 an  ……….. …1 000 ( 1,001)

Population au bout de 2 ans  ……….. …1 000 ( 1,001)²

Population au bout de « x » ans  ………1 000 ( 1,001)^x

 

 

 

 

 

Méthodes de calcul :

 

I )  Avec des adultes : nous pouvons  présenter  la recherche :

Il faut calculer  y = 1000 ( 1,001)^x    . On a là une fonction (y) exponentielle ; la variable « x » s’y trouve en exposant . Le calcul  s’effectue par logarithmes . On en déduit :

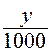 = ( 1,001)^x

 

log .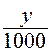 =  log. ( 1,001)^x

 

x . log 1,001  = log .

 

 

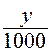
Si par exemple , on veut que la population ait doublé , il faut que

( 1,001)^x  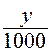=   =  2

 

donc , dans ce cas :

                             x . log 1,001  = log.2

Une table de logarithmes à 7 décimales donne :

Log. 1,001  = 0,000 4345     log 2 = 0,301029

On trouve donc :  x  = 0,301029 : 0,000 4345   = 693,493

 

                              x = 693  ans environ

AUTRES exemple de  PROBLEMES  « résolus »

 

PROBLEME  2               On donne : en 1998  il y a en France 60 000 000 de personnes .En quelle année la population aura-t-elle doublée (120 000 000 de personnes ) sachant que sa croissance annuelle est de  3%	1ère  solution :    On pose :      1,03n = 2 faire  , en faisant varier « n »   ou 2ème solution :   alors passer par les ..logarithmes 120 000 000 = 60 000 000 (1,03)n   soit n =   on a log . 120 000 000 =  log 60 000 000  = on fait la soustraction :              = on cherche le log 1,03 on doit effectuer la division d’un logarithme par un autre logarithme :
SUITE géométrique et intérêts composés
PROBLEME 3               Un capital de 9 000   Euros  à produit , capital et intérêts composés , une somme de 12 000  euros , le taux étant de 5 %. Combien d’année est-il placé ?	Solution :   On aura , d’après la formule :            12 000 = 9 000(1+0,5)n et en appliquant le calcul logarithmique :   n =   on a  log. 12 000 = 4,07918       log. 9 000 = 3,95424 donc : 4,07918 - 3,95424 reste :  log  0,12494   or log. 1,05 = 0,02119   On aura donc à effectuer la division d’un logarithme par un autre logarithme.  =  5 ans 10 mois environ

Problème N°4 : La première année de son ouverture au public , un musée est visité par 250 000 personnes. Durant les années suivantes on enregistre une diminution annuelle de 8 % du nombre de visiteurs.

a)        Quel a été , dans ces conditions, le nombre de visiteurs de la deuxième année ?  b)        Quel a été le nombre total de visiteurs au cours des deux premières années ?   Quel a été , dans ces conditions, le nombre de visiteurs de la cinquième année ?

 

 

 

TRAVAUX AUTO FORMATIFS.

 

CONTROLE :

 

 

Reprendre les exercices et modifier les valeurs de départs.

 

 

 

EVALUATION