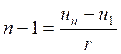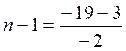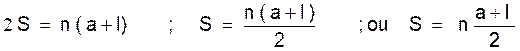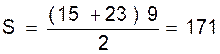|
Les suites et
ensembles de nombres |
ENVIRONNEMENT du
dossier:
|
2°) découverte : les
suites arithmétiques. |
Les SUITES ou PROGRESSIONS ARITHMETIQUES
Partie
1 :
I ) LA PROGRESSION
ARITHMETIQUE (définition).
II ) RECHERCHE DU Nième terme d’une progression .
III ) REPRESENTATION GRAPHIQUE D’UNE PROGRESSION
ARITHMETIQUE
IV)
EXERCICES et PROBLEMES RESOLUS
Partie 2 :
I ) SOMME D’UN CERTAIN NOMBRES DE TERMES CONSECUTIFS
D’UNE PROGRESSION ARITHMETIQUE
II ) SOMME des
n premiers TERMES CONSECUTIFS D’UNE PROGRESSION
ARITHMETIQUE.
III ) INSERTION DE
MOYENS ARITHMETIQUES
|
TEST |
COURS |
Interdisciplinarité
|
Exemple : Les
marches d’un escalier ont une hauteur de 17 cm . le
niveau de la première marche est situé à 5 cm au dessus
du sol . écrivons la suite des hauteurs atteintes par
les marches successives : 5 ; 22 ; 39 ; 56 ;
73 ; 90 ; 107 ; 114 .
Cette suite , dont chaque terme est obtenu en ajoutant
« 17 » au terme précédent, se nomme progression arithmétique. ( « 17 » est le nombre constant appelé
« raison »)
I ) LA PROGRESSION ARITHMETIQUE :
Définition : une
progression arithmétique est une suite de nombres appelés « termes » tels que chacun d’eux se déduit du précédent par addition
d’un nombre appelé
« raison ».
On dit
aussi que le terme suivant est égal à celui qui le précède ,
augmenté d’une quantité constante, que l’on appelle « raison » de la progression.
La progression est
« croissante » ou « décroissante suivant que la raison est positive
ou négative.
|
Exemple de progression croissante |
Exemple
de progression décroissante
|
|
2 ;7 ;12 ;17 ;22 ;27 ;32 est
une progression croissante de raison « 5 » |
20 ;
16 ; 12 ; 8 ; 4 est une progression décroissante de
raison « - 4 » |
|
Elle
s’énonce : 2
est à 7 comme 7 est à 12
comme 12 est à 17 ;etc. |
Elle
s’énonce : 20
est à 16 comme 16 est à 12 ; comme 12 est à 8 ;etc. |
|
Dans une progression croissante : r > 0 |
Dans une progression décroissante : r < 0 |
Si la
raison est nulle , tous les termes sont égaux.
Dans
les suites arithmétiques ( dites aussi "progressions arithmétiques" )
Chaque
terme noté "u" est égal au précédent augmenté d'une constante "b" (appelée "raison
de la progression" )
Autre façon de dire:
Si
u1 =u 0 +
b ( ainsi le
terme 1 est égal au terme u 0
plus la raison "b")
Si u2 = u1 + b ( ainsi le terme de
rang 2 est égal au terme 1 plus la raison "b")
Si
u3 = u2 +
b ( ainsi le
terme 3 de rang est égal au terme 2 plus la raison "b")
On désignera
le nième terme par un
le terme général.
Nous
en déduisons la forme générale :un = un-1+ b
On
appelle "r" la raison de la suite arithmétique ;chaque terme se
déduit du précédent en ajoutant le même nombre ( r) , sauf bien entendu le premier.
Et
l'on écriera :
|
un = un-1+
r |
Remarque : Si u0
vaut : 0
u1 =0 + b ( ainsi le terme 1
est égal à la raison "b")
u2 = b + b
( ainsi le terme de rang 2 est égal au terme 1
plus la raison "b")
u3 = u2 +
b = b +b +b = 3b (
ainsi le terme 3 de rang est égal au terme 2 plus la raison
"b")
Si on
désigne la raison par la lettre "r" : alors : on pourra écrire que
Si u0 =0 alors un = 0+ nr = nr
On retiendra que : la valeur d’un terme
quelconque d’une progression arithmétique est égal au 1er terme
augmenté d’autant de fois la raison qu’il y a de termes avant celui que l’on
calcule.
II ) RECHERCHE de la
valeur du Nième terme d’une progression .
Théorème : Dans
une progression arithmétique , un terme de rang
« n » est égal au premier , plus
(ou moins) autant de fois la
raison qu’il y a de termes avant lui.
|
Soit
« r » la raison et « n » le nombre des termes jusqu’à
« u » On
voit facilement que : Le
premier terme est « a » Le
deuxième terme est b = a + r Le
troisième terme est c =
b + r ou a + r + r
= a + 2 r Le
quatrième terme est d = c + r = b + r + r
= a + r + r +r = a + 3 r Si
l’on veut avoir le terme « u » , on aura
la formule : U
= a + ( n –1 ) r
|
|
Si
la progression arithmétique est décroissante la formule sera : U = a – ( n-
1) r
|
On
peut donc exprimer un en fonction de u1 ; r et
n :
Nous
avons vu précédemment que u = a + ( n –1 ) r
Si
U représente un (la
valeur du nième terme) ; « a » représente u1 (le
premier terme ): On
peut écrire un = u1 + ( n
–1 ) r
|
Exemple : Suite des nombres impairs
positifs : 1 ; 3 ;
5 ; 7 ; ……
C’est la progression arithmétique de premier terme u1
= 1 , de raison « 2 ».
Le 1 000ème nombre impair
est : u 1 000 = 1 + ( 999 x 2) = 1 999
Le n ème
nombre impaire est :
nn = 1 + 2 ( n - 1 ) = 2 n - 1
Activités : vérifier pour n = 1 ; 2 ; 3 ; 4
EXERCICES
TYPES :
a) Le premier terme étant « 5 » , la raison étant « 3 » , le terme de rang
« 18 » :
La valeur du 18ème terme est : 5 +
3 ( 18 - 1)
= 5 + 3 ( 17) = 56
b) Le premier terme d’une progression est
« 3 » , la raison est « 5 » , le
nombre « 528 » fait partie de
la progression , quel est son rang ?
« u = u1
+ r ( n - 1 ) » ;
« 528 =
3 + 5 ( n - 1 ) » ; « 528
= 3 + 5 n - 5 » ; « 528 = +
5 n - 2 » ; « 530
= + 5 n » ; « n =
530 / 5 » ; « n
= 106 » ;
conclusion : le nombre « 528 » est au rang
« 106 »
III )
REPRESENTATION GRAPHIQUE D’UNE PROGRESSION ARITHMETIQUE :
La représentation graphique d’une
progression arithmétique dans un repère
cartésien est une droite de la forme
« y = ax +b » où
« y = un » ; « a = r » ; x = (n -1) ;
b = u1 -1 ;
remarques :
« u1 » et « r » étant constants
, nn est une fonction linéaire de « n »
, de la forme « un = an + b » ( avec « a = r » et « b = u1
- r » ) . mais cette fonction n’est définie que pour les valeurs entières , positives de « n » ( n ![]() N
* ). Le graphe de cette fonction est donc constitué par une succession de
points alignés.
N
* ). Le graphe de cette fonction est donc constitué par une succession de
points alignés.
Exemple :Nombres impairs.
-
de nombreuses fonctions ,
dites linéaires , varient en réalité par paliers successifs. C’est ainsi que le
prix d’un billet de chemin de fer varie par tranches de 10 km. Le prix d’une
pièce d’étoffe ne peut varier que par paliers de 1 centime au minimum,
puisqu’il n’existe aucune unité monétaire inférieure à celle - ci .
On constatera sur de nombreux exemples que la
représentation d’une telle fonction par une droite n’est qu’approchée. En réalité , le graphe est constitué par une succession de
paliers figurant les termes d’une
progression arithmétique.
IV) EXERCICES et PROBLEMES RESOLUS :
un = u1 + ( n –1 ) r
Savoir reconnaître une suite
arithmétique et savoir calculer ses
éléments :
|
Exercices |
Solution : |
|
Soit
« u » la suite arithmétique de premier terme 3 et de raison 5 : Calculer u1 ;
u2 ; u 100 |
u1 = 3 u2
= 3 +5 =8 u 100= 3 + 5(100-1) = 3 + 99 fois5 =498 |
|
Soit
« u » la suite arithmétique de premier terme « u1 »=
12 et telle que u 25 =84 1)
calculer la raison de cette suite. 2)
Calculer u15 |
1)
u 25 = u1 + 24
fois r par
transformation on obtient : r = 2) u15 =
u1 +14 fois 3 = 12 +52 =64 |
|
Calculer le 21ème
terme de la progression : 5 ; 13 ; 21 ; 29 ;….. |
|
|
Calculer le 27ème
nombre impair . Les nombres impairs forment la
progression : 1 ; 3 ; 5 ; 7 ; …..de raison 2. |
|
PROBLEME 1: Quelle est la
hauteur d’une tour au dessus du sol, sachant que
l’on doit gravir 90 marches de 18 cm chacune au dessus
de la première , et que la première n’a que 15
cm. ? Solution : Le premier terme
de la progression est 15 cm ; la raison est de 18 cm. La progression
arithmétique serait : 15 ;
33 ; 51 ; 69 ;…x a ;
b ; c ;………….u La hauteur de la
tour est égale à la première marche
plus autant de fois 18 cm qu’il y a de marches au-dessus de la première , soit 90-1 = 89 On peut
écrire : x = 15 + 89 Ou
en appliquant la formule générale :
un = u1 + ( n –1 ) r
u = 15 + ( 90
– 1 ) 18 = 1617 |
|
4°) Soit
« u la suite arithmétique de premier terme « 3 » et de raison
« –2 » , sachant que un = -19 ,
retrouver « n » |
On sait que
un = u1 + ( n –1 ) r
Donc (n – 1 )
r = un - u1 Ce qui donne : Donc Conclusion :
n = 12 |
|
5°) Soit u la suite arithmétique telle que u 10 = 18,5 et u 25
= 48,5 Calculer le
premier terme de la suite et sa raison. |
Calcul de la raison : On peut savoir que : u 10 = u1+ 9 r et que u 25 = u1 +
24 r on peut donc
calculer u 25 - u 10 = (u1 + 24 r ) - (u1+ 9 r) = 15 r on sait que u 25-
u 10 = 48,5 – 18,5 = 30 donc on peut écrire : 15 r = 30 r = 2 calcul du
premier terme : on a vu
que : u 10 = u1+
9 r on en déduit que u1 =
u 10 - 9 r ; u1 =
18,5 – 9 fois 2 u1 =
18,5 – 18 u1 =
0,5 |
|
6°) soit
« u » la suite des nombres entiers impairs .Ecrire les 5 premiers
termes. Cette suite
est-elle arithmétique ? si oui quelle est sa raison ? Soit
« n » entier supérieur ou égal à 1 ,
exprimer « un » en fonction de n |
u1
=1 ; u2 =3 ; u3 = 5 ; u4
=7 ; u5 = 9 cette suite est
de raison : 2 un =
2n -1 |
COURS (partie 2)
Théorème 1 : dans toute progression arithmétique ,
un terme quelconque est égal à la moyenne
arithmétique ( demi - somme)
du terme qui le précède et de
celui qui le suit.
Si « a » ; « b » ; « c » sont
trois termes consécutifs d’une progression , dont la
raison est « r » on a :
« c = b + r » ;
« c = d - r » ; d’où
« 2c = b + d » et
I ) SOMME D’UN CERTAIN NOMBRES DE TERMES CONSECUTIFS
D’UNE PROGRESSION ARITHMETIQUE.
Théorème : Dans une progression arithmétique limitée ,
la somme de deux termes quelconques équidistants des extrêmes est constante et
égale à la somme des extrêmes.
En effet , le terme qui en a par
exemple « 3 » avant lui est égal à « a + 2r » ; celui
qui en a « 3 » après lui est égal à « l -
2r » , puisque « l »
est égal à ce terme plus « 2r » . Donc la somme des 2 termes considérés est « a + 2r + l - 2r = a + l »
Dans ces conditions , on comprend que l’on ait :
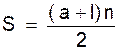
« n » étant le
nombre de termes ; « a »
et « l » sont les termes extrêmes de la progression arithmétique. (voir la démonstration ci dessous)
Démonstration : soit la progression arithmétique limitée de raison
« r », dont les termes extrêmes sont « a » et « l »
« a ; a + r ; a +
2r ; a + 3 r ; …(centre de la
progression)….. ; l - 3r ;
l - 2r ; l -
r ; l
on peut écrire que a + 3
r + l - 3r = a
+ l (sont des extrêmes )
ou a + 2 r + l - 2r = a
+ l (sont des extrêmes )
ou a +
r + l - r = a
+ l (sont des extrêmes )
Exemple :
soit la suite 2 ; 5 ;
8 ; 11 ; 14 ; 17 ; 20
[on identifie ( r = 3 ; a =
2 ; l = 20) ]
La somme des extrêmes = 2 + 20 =
22 ( a
+ l )
On remarque que :
|
( a +
r) + ( l - r) ® |
||
Généralisation :
à la somme des termes d’une progression arithmétique limitée.
Soit la progression arithmétique de « n » termes.
« a ; b ;
c ; d ; …………………………… …..; j ;
k ; l »
Nous pouvons écrire la somme des termes soit en commençant par le
premier terme , soit en commençant par le dernier
terme.
« S =
a + b
+ c + d + …………………………… …..+ j +
k + l »
« S = l +
k + j
+ i
+ …………………………… …..+ c
+ b + a
»
additionnons
membre à membre , il vient
« 2S
= (a + l )+ (b + k) + (c +
j) + …………..+ ( j + c ) + (k
+ b) + (l +a ) »
le second membre est la somme de « n » parenthèses. Chacune
étant la somme de deux termes équidistant des extrêmes est égala à « a + l » d’où :
Règle :
La somme des termes d’une progression arithmétique limitée est égale au produit
de la demi - somme des extrêmes par le nombre des termes.
Exemple 1 : calculer la somme des termes de la progression : 15 ;
24 ; 33 ; 42 ; 51 ; 60
( on reconnaît une suite arithmétique de
raison 9)
Solution :
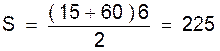
Exemple 2 : (la
première question a été traité dans le
chapitre précédent ) Des casiers de
même dimension sont empilés les uns sur les autres en formant une progression
arithmétique de raison 1 . Sachant qu’il y a 9 rangées de casiers et que la
rangée supérieure en contient 15 , combien en contient
la rangée inférieure ? Calculer
le nombres de casiers empilés .
Solution de la première partie : de la
formule : un = u1 + ( n –1
) r
un
= 15 ( 9
- 1 ) x 1
un
= 15 + 8 = 23
Solution : le premier terme ( la première
rangée ) vaut « 15 » le dernier terme ( la dernière rangée ) vaut
« 23» ; il y a « 9 » termes ( rangées)
|
|
Remarque 1 : la rangée du milieu est la demi - somme des rangées extrêmes quand le nombre de
rangées est impair.
Il suffit donc de compter les casiers de cette rangée qui est ici la 5ème , on trouve « 19 » et multiplier
ce nombre par le nombre de rangée
soit 19 fois 9 = 171
Remarque 2 : Si pour une cause quelconque (
encombrement par exemple) on ne peut compter que la première rangée et
le nombre de rangées , on calcule la
dernière rangée par la
formule : l
= a + ( n - 1 ) r
Du reste si nous remplaçons, dans
la formule de la somme , « l » par
cette valeur nous aurons :
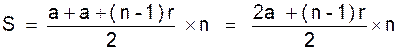
Exemple
1 . Calculer la somme des 30 premiers nombres
impairs :
S = 1
+ 3 + 5 + 7 +
…
Calcul :
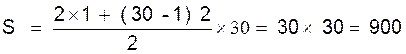
Remarque . Nous voyons que la somme des
« n » premiers nombres impairs est égal à « n² »
Exemple 2 :
calculer la somme des termes de la progression dont le premier
terme est « 5 » , la raison « 3 » et le nombre de termes
« 30 » .
Calcul :
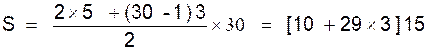
d’
où S = 1 455
II ) SOMME
des n
premiers TERMES CONSECUTIFS
D’UNE PROGRESSION ARITHMETIQUE.
Si S = u1
+ u2 + u 3 + …….+
un
Alors
Exemple : soit une
suite des 12 premiers nombres appartenant à la même suite arithmétique , dont
la valeur du premier vaut « 4 »
et le dernier vaut « 92 ». calculer
la valeur de la somme de ces 12 premiers nombres.
Solution : « n =
12 » ; « u1 = 4 » ; « u2=
92 » , on applique la formule : 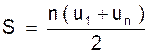
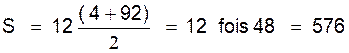
III) INSERTION DE MOYENS
ARITMETIQUES :
Problème 1 :Etant donnés deux nombres
« a » et « b » ,
insérer entre eux un certain nombre « n » de moyens
arithmétiques , c’est à dire former une
progression arithmétique de ( n + 2)
termes dont « a » et
« b » seront les extrêmes.
Pour
faire ce problème, il nous suffit de trouver la raison « r » de la progression .
Nous avons :
l = a + ( n + 2 - 1) r
Donc
l - a = ( n + 1 ) r
Et 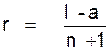
Exemple 1: Insérer « 7 »
moyens arithmétiques entre « 16 »
et « 48 »
Calcul de « r » :
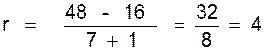
La progression sera :
16 ; 20 ; 24 ;
28 ; 32 ; 36 ; 40 ; 44 ; 48
C’est ce problème que nous
traitons sur le problème n°2 en interdisciplinarité .
Règle : la raison de
la progression obtenue par l’insertion de « n » moyens arithmétiques
entre deux nombres s’obtient en divisant la différence de ces nombres par le
nombre des moyens à insérer , plus un .
Exemple 2 : Insérer 6 moyens arithmétiques entre 10 et 24 ;calculer la raison et donner la progression :
Solution :
la
raison de la progression est : 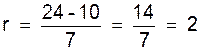
la progression est la suivante : 10 ; 12 ; 14 ;
16 ; 18 ; 20 ; 22 ; 24
……………………………………………………………………………………………………………………………………….
Traduire : un = un-1+ r
1 ) Donner une définition d’une suite
arithmétique :
2 ) Qu’appelle t on « raison » :
3 )Quand dit-on qu’une progression est « croissante ou «
décroissante » ?
4) quelle est la formule qui permet de
rechercher le Nième terme d’une progression ?
5 ) Quelle est la formule
qui permet de trouver (ou d’en déduire) le terme suivant dans une progression
arithmétique ?
EVALUATION :
Exercices :
Série 1
|
|
|
Soit « u » la suite arithmétique de premier terme 3 et de raison 5 : Calculer u1 ; u2 ; u 100 |
|
|
Soit « u » la suite arithmétique de premier terme « u1 »=
12 et telle que u 25
=84 3)
calculer la raison de cette suite. 4)
Calculer u15 |
|
Série 2
|
|
|
1 ) Le
millième terme de la progression arithmétique de raison |
|
|
2°) La suite des nombres impairs
est une progression arithmétique de raison 2 dont le premier terme es
1 : tel que 1 ; 3 ;7 ;9 ;11 ;13 ..; donner le modèle
mathématique. |
|
|
3°) on recherche la raison
« r » d’une progression : on connaît : le premier terme
= 2 , le 50 ième
terme = 149 |
|
|
4°) Soit « u la suite arithmétique de premier terme
« 3 » et de raison –2 , sachant que un
= -19 , retrouver « n » |
|
|
5°) Soit u la suite
arithmétique telle que u 10
= 18,5 et u 25 = 48,5 Calculer le premier terme de la suite et sa raison. |
|
|
6°) soit « u » la suite des nombres entiers impairs .Ecrire
les 5 premiers termes. Cette suite est-elle arithmétique ? si oui quelle est sa
raison ? Soit « n » entier supérieur ou égal à 1 ,
exprimer « un » en fonction de n |
|
|
Quelle est la hauteur d’une tour au
dessus du sol, sachant que l’on doit gravir 90 marches de 18 cm
chacune au dessus de la première
, et que la première n’a que 15 cm. ? |
|
PROBLEME 2: 5 disques métalliques
étagés forment un cône et sont en
progression arithmétique. Le plus grand disque a un diamètre de 240 mm et la
plus petite 80 mm. Calculer la raison de la
progression et déterminer le diamètre
des 3 autres disques. : |
|
PROBLEME 3:
Des casiers de même dimension sont empilés les uns sur les autres en formant
une progression arithmétique de raison 1 . Sachant
qu’il y a 9 rangées de casiers et que la rangée supérieure en contient 15 , combien en contient la rangée inférieure ? |
Problème 4 : (sciences : Info plus )
Un mobile de déplace librement à Paris 4,90 m pendant la première
seconde et successivement 9,80 m de plus pendant chacune des secondes qui suivent . Quel chemin parcourt -il pendant la cinquième seconde ?
Problème 5 : Un bureau
d’études est chargé de mener à bien le
projet de construction d’une pyramide ( base carrée
) du style de celle du Louvre.
Combien de plaques de verre , toutes identiques
et ayant la forme de triangles équilatéraux , sont - elles nécessaire à la réalisation
d’un ouvrage constitué de 12 niveau ?
Info :
« u1 » le
nombre de plaques constituant le niveau le plus haut ; (
4 plaques : 4 côtés ; 1
triangle)
« u2 » le nombre de plaques du niveau sous -
jacent ;
« Un » le nombre
de plaque du nième niveau sous- jacent ;
1°) S’aider
d’un dessin pour trouver la valeur de la raison :
..............................
2°) Déterminer : u 12 avec la formule « un = u 1 + ( n - 1 )
r » ;
3°) Calculer le nombre de plaques nécessaire à l’édification de cette
pyramide de 12 niveaux.
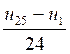
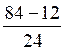
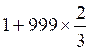 = 667
= 667