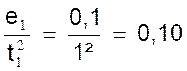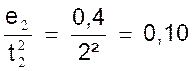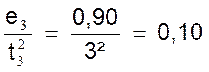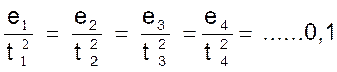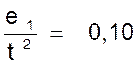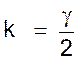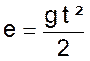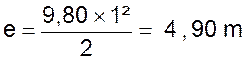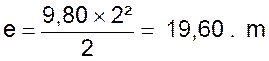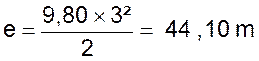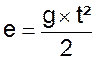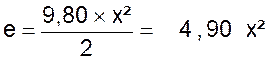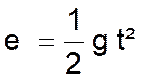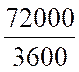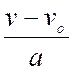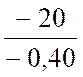Mouvement uniformément varié

Pré requis:

« mouvement »

ENVIRONNEMENT du dossier:

Index

Objectif précédent :

Le mouvement uniforme

Objectif suivant

1°) Le mouvement circulaire.

2°) Vers le « second degré »

tableau

Sciences :liste des cours

DOSSIER : MOUVEMENT UNIFORMEMENT VARIE

	I ) Etude expérimentale des espaces parcourus par une bille sur un plan incliné dans un cas simple.
	2 - Etude expérimentale de la vitesse de la bille roulant sur un plan incliné
	Vitesse instantanée
	Accélération.

	Partie 2 : la chute des corps .

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

Remarque : dans la vie courante , lorsque nous prenons un véhicule et que nous circulons sur une route , nous sommes toujours en situation d’accélération ou de décélération , notre « vitesse instantanée » change continuellement , voilà pourquoi on établit une vitesse moyenne après avoir effectué une « certaine » distance en fonction d’une durée connue (mesurée »

Ainsi ; effectuer un parcours à une vitesse moyenne de « 60 km par heure, signifie que pendant ce parcours on a pu rouler à une vitesse de 140 km /h et parfois à une vitesse de 30 km /h , il se peut qu’au cours de ce trajet on a dû s’arrêter pour une raison ou une autre . (route sinueuse et dangereuse , feu rouge ; panneau « stop » ; « arrêt pipi » ; blocage dans une file de voiture ; bouchon ; accident ; panne ; ….., mettre de l’essence dans le réservoir , se restaurer , …..….)

COURS

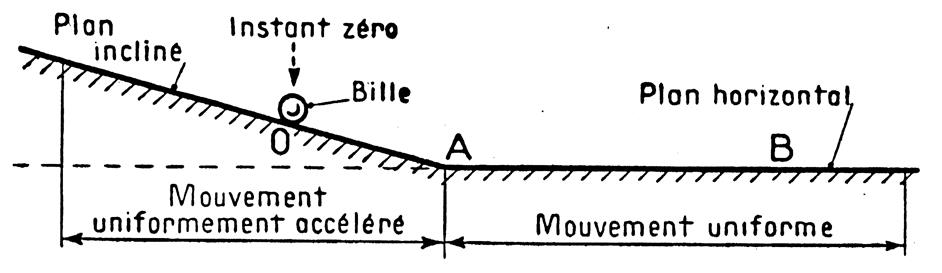
Faits d’observation :

Vous avez déjà descendu une rue en pente en vélo , descendu une pente en luge. Vous avez déjà fait rouler une bille sur une planche inclinée. La descente se fait de plus en plus vite . Les vitesses ne sont pas constantes . Les mouvements ne sont pas uniformes.

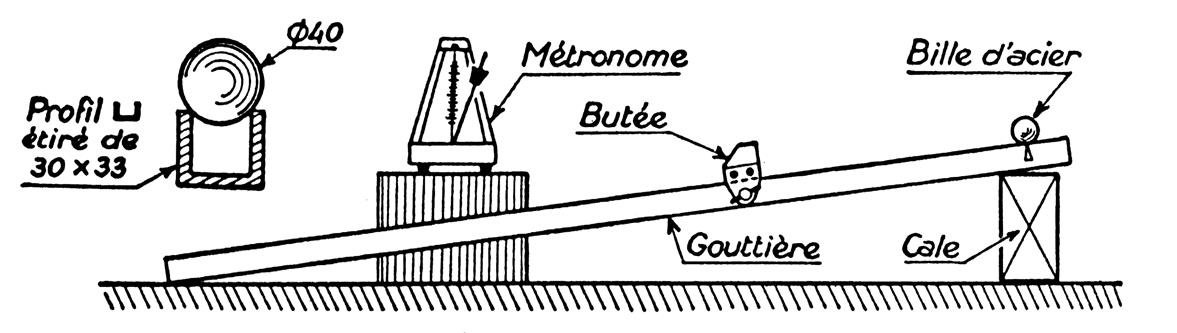
L’étude qui suit porte sur un mouvement analogue : celui d’une bille d’acier roulant sur un plan incliné.

I ) Etude expérimentale des espaces parcourus par une bille sur un plan incliné dans un cas simple.

a) Dispositif expérimental : Le plan utilisé peut être : soit une face bien dressé d’un chevron en bois sur lequel deux baguettes rectilignes parallèles forment une sorte de gouttière qui guide la bille, soit deux tiges de fer rond assemblés parallèlement et formant également une gouttière , soit un profilé en « U » de deux mètres de longueur..

Montage : Dispositif expérimental permettant d’étudier le mouvement de la bille sur le plan incliné. (Les frottements de la bille sur le profilé sont négligeables).

Un buttoir peut glisser le long du profilé. Il permet d’arrêter la bille à un instant fixé par un battement d’un métronome battant la seconde.

b) Expériences : On mesure l’espace parcouru par la bille pendant 1 s. ; puis pendant 2s. etc. …….. ; l’origine des distances sera au point de départ de la bille.

Lâchons la bille , sans la lancer, à l’instant précis d’un battement du métronome en comptant « 0 » et cherchons , en répétant plusieurs fois l’expérience , la position du butoir telle que la bille frappe juste à l’instant du battement suivant compté « 1 »et mesurons l’espace parcouru e₁ = 0,1 m.

(nota : il faut s’habituer au rythme du métronome : pour nous habituer au rythme du métronome , nous comptons à haute voix : 3 ; 2 ; 1 ; 0 ; 1 ; 2 ; la bille est lâchée à l’instant « 0 ».)

Mesurons ainsi les distances parcourues pendant : 1 ; 2 ; 3 ; 4 s.

Les mesures sont regroupées dans le tableau suivant :

Temps ………	t ₀ = 0	t ₁ = 1 s	t ₂ = 2 s	t ₃ = 3 s	t ₄ = 4s	t ₅ = 5s
Distances ou espaces parcourus…..	e ₀ = 0	e₁ = 0,10 m	e₂= 0,40 m	e ₃ = 0,90 m	e ₄ = 1, 60 m	e ₅ = 2,50 m

c) Interprétation des résultats :

1°) Les distances parcourues ne sont pas proportionnelles aux temps employés à les parcourir ; le mouvement n’est pas uniforme.

2°) Si nous divisons chaque espace parcouru par le « carré » du temps correspondant , le quotient est toujours le même :

En désignant par e _t l’ espace parcouru au bout de « t » secondes , nous avons donc :

ou e ₁ = 0,10 t ²

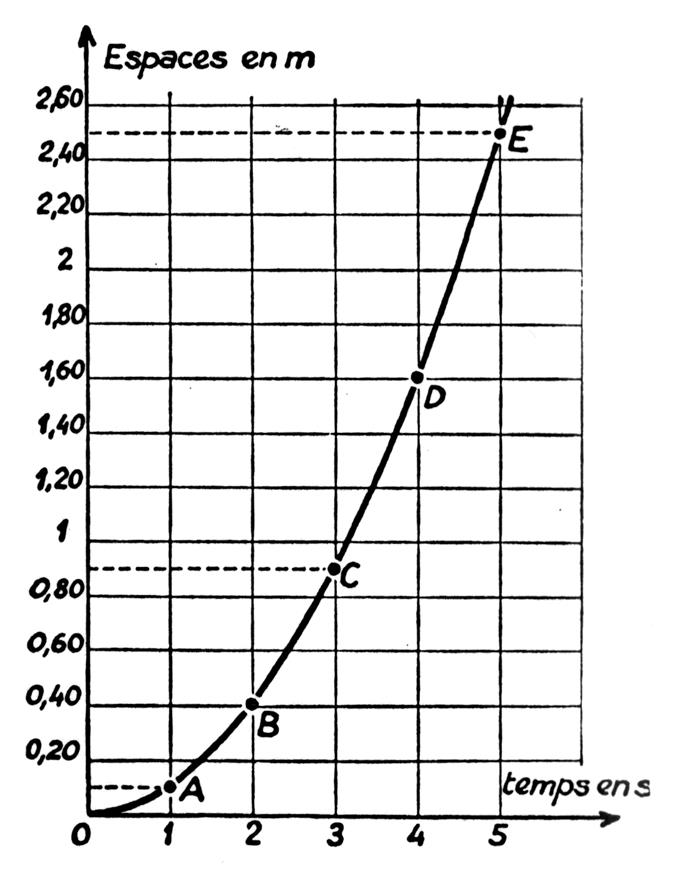
Ci dessus , le diagramme des espaces parcourus par la bille sur le plan incliné.

Cette courbe OABCDE est une parabole.

L’espace parcouru par la bille est proportionnel au carré du temps mis à le parcourir.

3°) Si nous recommençons l’expérience avec une autre inclinaison du plan, nous trouvons que l’espace parcouru est toujours proportionnel au carré du temps à le parcourir ; mais le coefficient de proportionnalité n’est plus égal à 0,10 . Il augmente à mesure que la pente du plan est plus grande.

On peut toujours écrire la formule générale : (1) e _t = k . t²

« k » étant un coefficient qui dépend de la pente du plan : plus la pente est grande , plus le coefficient « k » est grand .

d) Diagramme des espaces parcourus . (voir ci dessus )

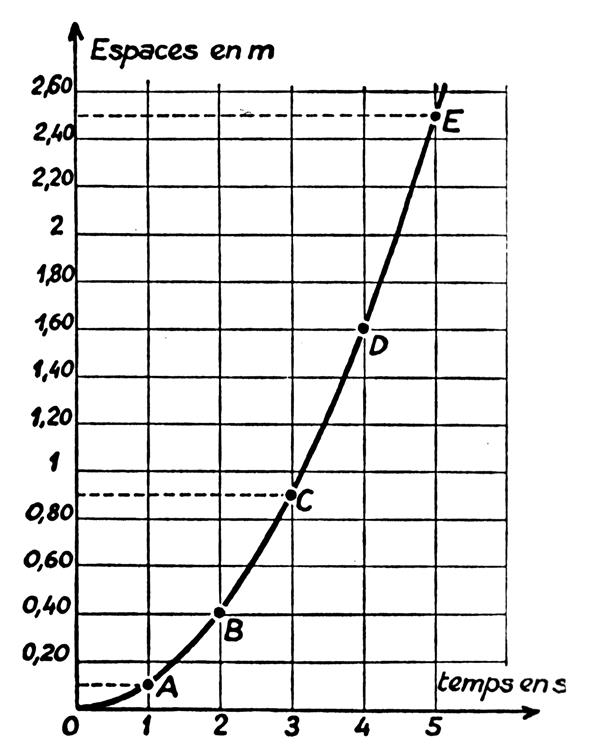
Si nous avons représenté graphiquement les résultats en portant :

- en abscisse , les temps ( échelle 10 mm pour 1s)

- en ordonnée , les espaces parcourus ( échelle :25 mm pour 1 m)

nous obtenons une courbe qui à la forme d’une parabole. ( attention : il ne faut pas confondre cette parabole (représentation graphique de nos mesures) avec la trajectoire, qui est une droite.)

3 - Etude expérimentale de la vitesse de la bille roulant sur un plan incliné.

« Vitesse instantanée » :

a) Dispositif expérimental - Nous plaçons à la suite de la gouttière précédente , et à la partie inférieure , une gouttière identique mais horizontale .

b) Nous recommençons une série de mesures dans les mêmes conditions que précédemment et nous étudions le mouvement de la bille sur le plan horizontal , avec une durée de roulement de « 1 s » sur le plan incliné.

Résultats des mesures :

Durée du roulement sur le plan incliné……………………………………..		1 s
Espace parcouru sur le plan incliné ……………………………………….		0,10 m
Espace parcouru sur le plan horizontal ……….	Pendant 1s	0,20 m
	Pendant 2 s	0,40 m
	Pendant 3 s	0,60 m

La vitesse de la bille sur le plan horizontal est constante « 0,20 m / s » . C’est la vitesse de la bille a l’instant où elle passe au point « A » du plan incliné . On dit que c’est la vitesse instantanée de la bille au point « A ».

Par définition : La vitesse instantanée , à l’instant « t » , d’un point mobile est la vitesse que ce point garderait si, à partir de cet instant, son mouvement devenait uniforme.

c) Nous recommençons une seconde série de mesures dans les mêmes conditions que précédemment avec une durée de roulement de « 2 s » de la bille sur le plan incliné ( pente de 10 % : k = 0,1) et nous étudions le mouvement de la bille sur le plan horizontal .

Résultats des mesures :

Durée du roulement sur le plan incliné……………………………………..		2 s
Espace parcouru sur le plan incliné ……………………………………….		0,40 m
Espace parcouru sur le plan horizontal ……….	Pendant 1s ……………………………………	0,40 m
	Pendant 2 s ………………………………….	0,80 m
	Pendant 3 s …………………………………	1,20 m
*Vitesse de la bille sur le plan horizontal…………………………………………*		*0,40 m/s*

Si nous refaisons une série de mesure avec une durée de roulement de la bille sur le plan incliné nous pourrons remarquer que la vitesse de la bille est de 0,60 m /s.

Ainsi nous pouvons regrouper « ces vitesses » à la sortie du plan incliné : nous les appelons : « valeurs de la vitesse instantanée » elles sont :

	La vitesse est de :	Qui correspond au calcul :
Vitesse instantanée à l’instant « t = 0 »	« v₀ = 0 »	= 2 ´ 0,10 ´ 0
Vitesse instantanée à l’instant « t = 1 »	« v₁ = 0,20 m/s »	= 2 ´ 0,10 ´ 1
Vitesse instantanée à l’instant « t = 2 »	« v₂ = 0, 40 m/s »	= 2 ´ 0,10 ´ 2
Vitesse instantanée à l’instant « t = 3 »	« v₃ = 0, 60 m/s »	= 2 ´ 0,10 ´ 3
Vitesse instantanée à l’instant « t »	« v_t = »	= 2 ´ 0,10 ´ t

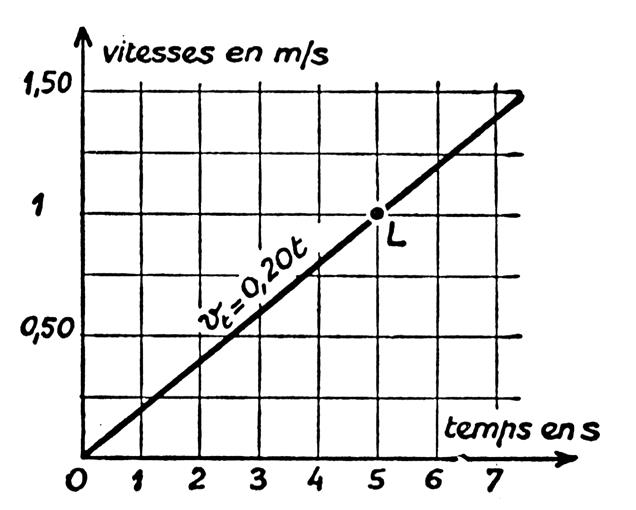
On remarque que la vitesse « v _t » , à l’instant « t » , ou « vitesse instantanée », est donc donnée par la formule : (2) « v _t = 2 k . t » ; Cette vitesse croît proportionnellement au temps.

Représentation graphique de cette vitesse :

La vitesse augmentant à chaque instant , le mouvement de la bille sur le plan incliné est dit « mouvement accéléré ».

IV ) Définition de l’accélération :

Les résultat précédents montrent que la vitesse de la bille augmente pendant chaque seconde , de la quantité constante de « 0,20 m /s) .

Cet accroissement de vitesse pendant chaque seconde est appelé « accélération » du mouvement.

Dans le cas d’une bille qui descend sur un plan incliné , l’accélération est constante , le mouvement est dit « uniformément accéléré ».

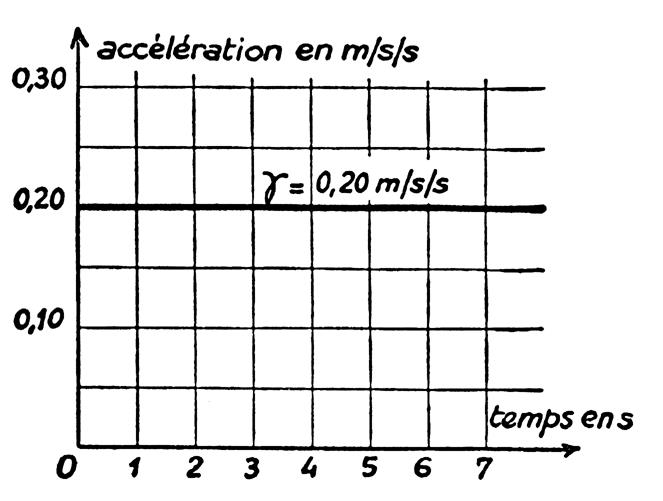
Dans un mouvement rectiligne uniformément accéléré , l’accélération est la quantité constante dont la vitesse s’ accroît pendant chaque unité de temps .

On la représente habituellement par la lettre grecque γ ( gamma)

(voir ci dessous le diagramme des accélérations)

Généralisons :

Représentation graphique de « gamma » = 0,20 m /s/s.

Dans les exemples précédents :

γ = 20 m / s par seconde , ce que nous écrirons γ = 20 m / s / s .

La formule v _t = 2 k . t donne pour les valeurs de « v » aux divers instants 0 ; 1 ; 2 ; ……

v ₀ = 0 ; v ₁ = 2 k ; v ₂ = 4 k ; v ₃ = 6 k ; ……

Pour chaque seconde , la vitesse augmente de « 2 k »

(1) Donc γ = 2 k = constante.

L’accélération est graphiquement représentée par une droite parallèle à l’axe des temps ; on l’appelle « diagramme des accélérations »

Résumé des formules du mouvement uniformément accéléré découlant de l’étude précédente.

Avec les conventions de simplification faites :

- la bille part au repos sans être lancée ;

- les espaces parcourus sont mesurés à partir du point de départ ,

- Les temps sont mesurés à partir de l’instant du départ ;

Dans (1) Remplaçons « k » par sa valeur les formules deviennent :

(1)

e _t = k . t²

_devient

e _t = . t²

(2)

« v _t = 2 k . t »

_devient

v _t = γ . t

(3)

γ = 2 k

_devient

γ = constante

- En résumé :

1°) l ’espace parcouru par une bille qui roule sur un plan incliné dans les conditions simplificatrices suivantes :

- la bille part au repos sans être lancée ;

- les espaces parcourus sont mesurés à partir du point de départ ,

- Les temps sont mesurés à partir de l’instant du départ ;

est e _t = k . t² (1)

2°) Le diagramme des espaces parcourus est une parabole tangente à l’axe des temps à l’origine des coordonnées.

3°) La vitesse instantanée de la bille est celle qu’elle garderait si , à partir de l’instant considéré , son mouvement devenait uniforme.

4°) Cette vitesse est proportionnelle au temps : v _t = 2 k . t ( 2)

5°) le diagramme des vitesses est une droite passant par l’origine des coordonnées.

6°) L’accélération « gamma » , ou accroissement de la vitesse par unité de temps , est constante. γ = 2 k = constante

son diagramme est une droite parallèle à l’axe des temps.

7°) Les formules ( 1) et (2) peuvent s’écrire :

e _t = . t² et v _t = γ . t

- PARTIE 2 : La « Chute des corps » :

Des expériences ont montré que le mouvement de la chute d’un corps dans le vide est un mouvement rectiligne uniformément accéléré. Dans l’air , cette loi n’est plus vérifiée. Il faut tenir compte de la résistance de l’air qui s’oppose à la chute des corps. Dans un souci de simplification, nous supposerons que cette résistance est négligeable .

a) Accélération : l’accélération de tous les corps en chute libre se représente par la lettre « g » et vaut à Paris 9,81 m.s ^-2, ( = 9,81 m / s² )

g = = 9,81 m / s²

Recherche de la définition de l’accélération :

On demande de calculer l’espace parcouru par un corps qui tombe : pendant la première seconde ; puis après deux secondes , puis après trois secondes, etc.

On ne tiendra pas compte de la résistance de l’air.)

Solution :

D’après la formule on a : ( « g » représente l’accélération soit 9,80 m /s²)

Après la première seconde :

Après la deuxième seconde :

Après la troisième seconde :

Et ainsi de suite :

Nous pouvons représenter graphiquement cette fonction :

devient

qui est de la forme y = a x² où « a » est représenté par « 4,90 »

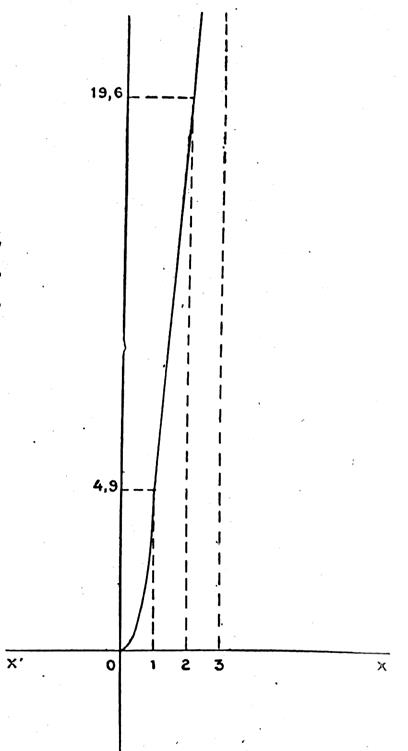
La courbe ci dessous représente la courbe de la chute des corps.

En remplaçant « x » et « y » par leurs valeurs ci dessus , et en portant celles - ci sur les axes on obtient des points d’intersections . Si l’on joint ceux ci on trouve la moitié d’une parabole ; car ici , on ne peut pas envisager des valeurs négatives de « x » . (comme au Pb N°1 précédent).

Commentaires : 1 : le coefficient de « x² » est ici « 4,9 » représenté par « a » qui est donc un nombre positif.

La parabole n’aura donc que la branche positive.

Commentaire 2 : cette branche appartient à une parabole qui est effilée , si l’on peut dire qu’une parabole dont le coefficient de « a » serait égal à « 1 ».

La courbe précédente est la courbe de la chute des corps.

On peut y vérifier que les vitesses après chaque seconde sont proportionnelles aux temps passés , ce qui se montre expérimentalement en Physique.

Effectivement :

L’ accélération :

Dans la première seconde , l’espace parcouru a été de 4,90 m .

Dans la deuxième seconde , cet espace a été de 19,60 m - 4,90 m soit de 14,70 m ; c’est à dire de 4,90 m + 9,80 m , après la première seconde la vitesse a donc augmenté de 9,80 m.

Dans la troisième seconde , l’espace parcouru a été de 44,10 m - 19,60 m soit de 24,50 m , c’est à dire 4,90 m + 17,60 m ou bien de 4,90 m + 2 fois 9, 80 m et ainsi de suite .

La vitesse augmente de 9,80 m à chaque seconde. Ce nombre est appelé l’ accélération.

b) Vitesse à l’instant « t » :

La vitesse à l’instant « t » est

v = g t

« v » en m /s

« g » = 9,81 m / s²

c) Espace parcouru .

En prenant :

- pour origine des temps, l’instant où le corps est lâché,

- pour origine des espaces, le point où le corps est lâché ,

l’espace parcouru à un instant « t » est :

où : « e » est exprimé en en mètres ; « g » vaut 9,81 m /s² et « t » est exprimé en secondes.

II ) Cas générale : Le mouvement uniformément varié

V = v _o+ a t

"V " est la vitesse au temps "t"

"V _o " est la vitesse initiale

"e" désigne l' espace parcouru

"a" désigne l' accélération du mouvement

"t" temps mis

e = v _ot + a t ²

"V _o " est la vitesse initiale

"e" désigne l' espace parcouru

"a" désigne l' accélération du mouvement

"t" temps mis

Si le corps part du repos :

v_o = 0 ; alors les formules deviennent:

V = v_o+ a t devient V = 0 + a t ;

e = v_ot + a t² devient e = 0t +a t²

V = a t

e = +a t²

Problème résolu n° 1:

Au départ d'une gare un train met 40 secondes pour atteindre sa vitesse uniforme de 72 kilomètres à l'heure. Pour s'arrêter , il ralentit sa vitesse de 0 ,40 m/s^-1

On demande :

1° ) L' accélération du mouvement de départ.

2°) L'espace parcouru quand il atteint sa vitesse normale;

3°) Le temps mis pour s'arrêter;

4°) La distance de la gare d'arrivée à laquelle le mécanicien doit cesser l'admission de vapeur.

Solution :

1° L' accélération du mouvement de départ v = a t , d'où a =

v = 72 kilomètres à l'heure ou 72 000 mètres en 3600 secondes

ou = 20 mètres à la seconde

a = = 0,50m par seconde

2° ) L'espace parcouru quand il atteint sa vitesse normale :

e = +a t² ; e = + 0,50 40² = 400 mètres.

3°) Le temps mis pour s'arrêter :

V = v_o+ a t de cette formule nous tirons : t =

mais v = 0 correspond à l' arrêt ; v_o = vitesse initiale 72 kilomètres à l'heure ou 20 mètres à la seconde ; a = - 0,40 m accélération "retardatrice".

t = ; t = ; t = 50 secondes

4°) La distance de la gare d'arrivée à laquelle le mécanicien doit cesser l'admission de vapeur.

e = v_ot +a t² ; e = 2050 + (-0,40) 50²

e = 1000-500 = 500 mètres

CONTROLE :

Compléter les phrases suivantes :

1 °) l ’espace parcouru par une bille qui roule sur un plan incliné dans les conditions simplificatrices suivantes :

- la bille part au repos sans être lancée ;

- les espaces parcourus sont mesurés à partir du point de départ ,

- Les temps sont mesurés à partir de l’instant du départ ;

est (Donner la formule) …………………….(1)

2°) Le diagramme des espaces parcourus est ……………………………….

3°) La vitesse instantanée de la bille est celle qu’elle garderait ……………………………………………………………………………………………

4°) Cette vitesse est ……………………….. : Formule ( ?) : ………………….. ( 2)

5°) le diagramme des vitesses est ……………………………………………………

6°) L’accélération « gamma » , ou accroissement de la vitesse par unité de temps , est : ……………………... Formule ?: ……………………………..

son diagramme est …………………………………………………….

7°) Traduire les formules suivantes , à quel calcul sont -elles destinées .

e _t = . t² et v _t = γ . t

EVALUATION

1°) Un pétrolier met 33 minutes pour s'arrêter , il parcours un distance de 5 km.

2°) Un train rapide , faisant le trajet de Paris au Havre , part de Paris à 14 h 15 , passe à Rouen à 15 h 28 et arrive au Havre à 16 h 15 .

Quelle est la vitesse moyenne d’un point du train : entre Paris et Rouen , en Rouen et le Havre ? entre Paris est le Havre ?

3°) La vitesse instantanée d’un train est de 112 km /h à 14 h 25 , de 118 km/h à 14 h 58 et de 114 km /h à 15 h 12 . Quelle est l’accélération moyenne : entre 14 h 25 et 14 h 58 ? entre 14 h 58 et 15 h 12 ?

Que pensez vous du mouvement du train dans ce dernier intervalle de temps ?

4°) Deux corps tombent d’un même point « O » à « 1 s » d’intervalle.

a) Après quel temps seront - ils séparés l’un de l’autre de 24 , 5 m ?

b) Quels chemins auront -ils parcours à ce moment - là ? ( g = 9,8 m /s / s)

5°) Un cycliste démarre d’un mouvement uniformément accéléré γ = 1 m / s / s.

a) Combien de temps met -il pour avoir une vitesse de 20 km/h ?

b) Quelle distance a - t- il parcourue pendant ce temps ?

c) Quelle a été sa vitesse moyenne pendant ce démarrage ?

6°) Un automobiliste roule à la vitesse de 90 km /h . Le conducteur , apercevant un obstacle , coupe les gaz et freine énergiquement. La vitesse de la voiture diminue de 5 m/s pendant chaque seconde.

a) Quelle est la vitesse de l’automobile 3s après le début du freinage ?

b) Quelle est la distance parcourue pendant ces 3 s ?

c) Combien de temps met -il pour s’arrêter ?

d) Quelle distance a - t -il parcourue pendant ce temps ?

Remarque : la diminution de la vitesse pendant cha&que seconde est appelée « décélération » . Elle est constante dans ce problème, c’est pourquoi le mouvement est dit « uniformément retardé ».

7°) Au départ d'une gare un train met 40 secondes pour atteindre sa vitesse uniforme de 72 kilomètres à l'heure. Pour s'arrêter , il ralentit sa vitesse de 0 ,40 m/s^-1

On demande :

a ) L' accélération du mouvement de départ.

b) L'espace parcouru quand il atteint sa vitesse normale;

c) Le temps mis pour s'arrêter;

d) La distance de la gare d'arrivée à laquelle le mécanicien doit cesser l'admission de vapeur.