DOC. : Professeur ; Formateur

DOC : Formation Individualisée LA PARABOLE.

DOC : Elève.

I ) Pré requis:

i9	Notions	:i
i9	Les ensembles de nombres	:i
i9	Les tableaux numériques à doubles entrées	:i
i9	Fonction et application	:i
i9	Les repères cartésiens	:i

DOSSIER N° : Matière : MATHS  Leçon : LES FONCTIONS

Information « TRAVAUX » Cliquer sur le mot !.

INFORMATIONS PEDAGOGIQUES :

Savoir construire une parabole dans un repère cartésien

Equation de la forme : ² ; cas avec : et cas avec

NIVEAU : Formation Niveau V (BEP) %ºliste des savoirs et savoirs faire.

OBJECTIFS : - définir une parabole et Savoir identifier et tracer ² ; (avec « a » = 1)

II ) ENVIRONNEMENT du dossier :

Index		Dossier précédent : -1° Cours niveau V -2° Fonction généralités. -3° Représentation type. 4°) résoudre l’équation de la forme ax² + b = 0			Dossier suivant : 1°)Etude de la fonction « ax² + bx +c » 2°)Tracés niveau B E P . 3°) Exemples de tracés. 4°) Les fonctions (présentation) 5°) Voir l’étude graphique d’une fonction numérique .			Info : Ici : Info plus le tracé de la fonction « ² » et « ² »…..
Test	COURS		Travaux auto - formation.				Corrigé des travaux auto - formation.
			Contrôle	évaluation		INTERDISCIPLINARITE	Corrigé Contrôle		Corrigé évaluation

V ) DEVOIRS ( écrits):

Devoir diagnostique L tests.	
Devoir Auto - formatif (intégré au cours)	
Devoir Formatif « Contrôle : savoir » ; (remédiation)	
Devoir Formatif «  Evaluation  savoir faire » (remédiation)	
Devoir sommatif.	
Devoir certificatif : (remédiation)	

* remédiation : ces documents peuvent être réutilisés ( tout ou partie) pour conclure une formation .

Leçon	Les études de FONCTIONS :
Niveau V ; IV	Savoir construire une parabole dans un repère cartésien.

La Fonction « a x² » est une fonction dite : « paire » : (puissance « paire »)

COURS

Rappel  sur l’écriture utilisée :

Le mot « Fonction » :est noté « »

La lettre «  » est appelée « variable ». (ce sera un nombre pris dans un ensemble de nombre)

Pour l’écriture « f (x) » ; lire «  éffe de ixe » ; comprendre « en fonction de x »

Pour passer de « x » à « f(x) » on a besoin d’une relation mathématique  notée : R

Cette relation  « R » est une expression algébrique exprimée avec la variable « x », cette expression est le deuxième membre de l’égalité de la forme y = …f (x)

Soit l’écriture : x f (x)

Convention d’écriture : La flèche à talon : « » doit se traduire par : «à pour image »

on doit lire  : «  ixe a pour image  « éffe » de « ixe »  »

exemple soit l’équation «  » pour «  » on trouve « y = 20 » ;

ainsi pour 5 20 on lit : pour «5 » (nombre appartenant aux nombres de l’ensemble de départ) on obtient « 20 » (nombre appartenant aux nombres de l’ensemble d’arrivée)

ainsi pour :

« »	« a pour image »
-2		-8
1		4
2		8
7		28
8,4		33,6

On peut prolonger le tableau suivant :

	Egale
	=	- 8
	=	4
	=	8
	=	28
	=	33,6

ACTIVITE : TRACE de la « Parabole » :

Calculer les carrés des nombres entiers consécutifs, en commençant par l’unité. ( complétez le tableau )

Carré de 1 égale	1 ´ 1 = 1 ² = 1
Carré de 2 égale	2 ´ 2 = 4
Carré de égale	3 ´ 3 = 9
Carré de égale	´ =
Carré de égale	´ =
Carré de égale	´ =
Carré de égale	´ =
Carré de égale	´ =
Carré de égale	´ =
Carré de égale	´ =
Carré de égale	´ =
Carré de égale	´ =

On trouverait ainsi les carrés des « n » premiers nombres. (appelés aussi « carrés parfaits ».)

Nous remplaçons les nombres par la lettre générale « x » , le carré de ces nombres sera représenté par la lettre «  » , et l’on aura : ²

Construisons le graphique de cette fonction , «  » étant la variable et prenant les valeurs 1 ; 2 ; 3 ; 4 ; …….etc.

On obtiendra pour les valeurs correspondantes de «  » : 1 ; 4 ; 9 ; 16 ; ….etc. ;

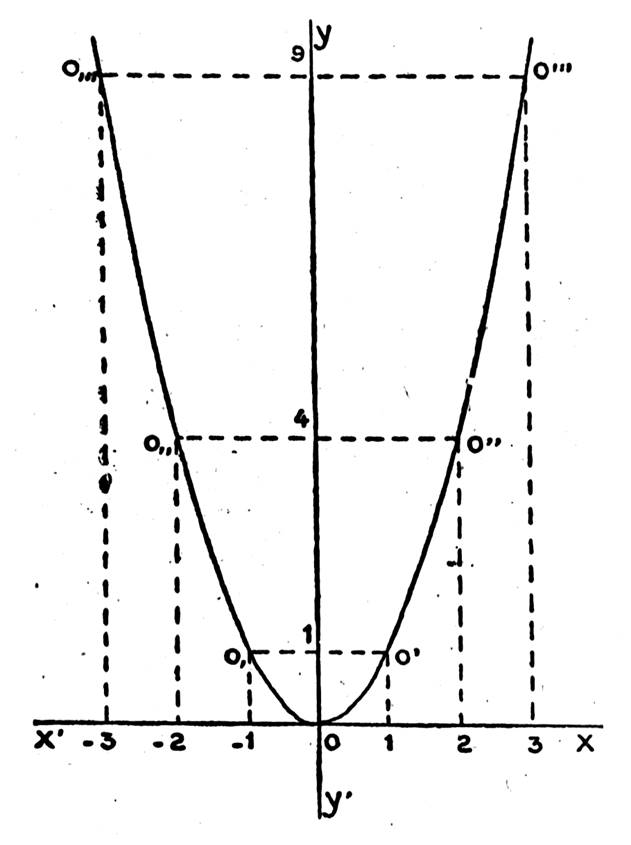
En portant ces valeurs sur les deux axes ( voir « repère cartésien) )

On obtient des points d’intersection O’ ; O’’ ; O’’’

Joignons ces points. On voit qu’on n’obtient plus une droite , mais une courbe d’une « forme spéciale ».

Donnons maintenant à « x » des valeurs négatives , soit : -1 ; - 2 ; - 3 ; -4 , les valeurs correspondantes de « y » seront : + 1 ; + 4 ; + 9 ; +16 ; ….etc. ( ici : SOS calculs ) et la courbe représentative sera la ligne O_, ; O,, ; O ,,, .;

On remarque que cette portion de courbe est absolument le symétrique de la portion de courbe O’ ; O’’ ; O’’’

Les deux portions de courbes n’en forment qu’une, Cette courbe est tangente à l’axe « x’ x » en « O »

En géométrie, cette courbe est appelée « parabole ».

On définit la parabole ainsi :

La distance d’un point de la parabole à l’axe «   » est proportionnelle au carré de la distance de ce point à l’axe «  » 

(voir une explication avec l’ exemple : exercice n°1 sur la chute des corps)

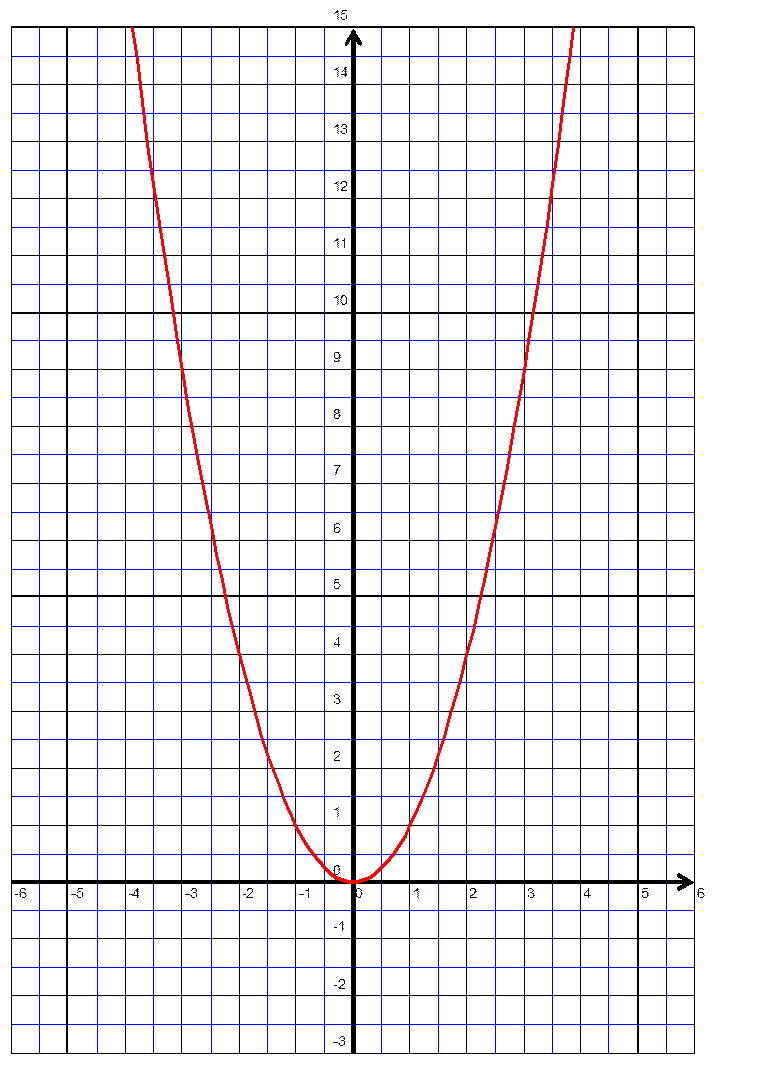
h (x) = x² ; de la forme « y = a x² » , avec « a = 1» positif

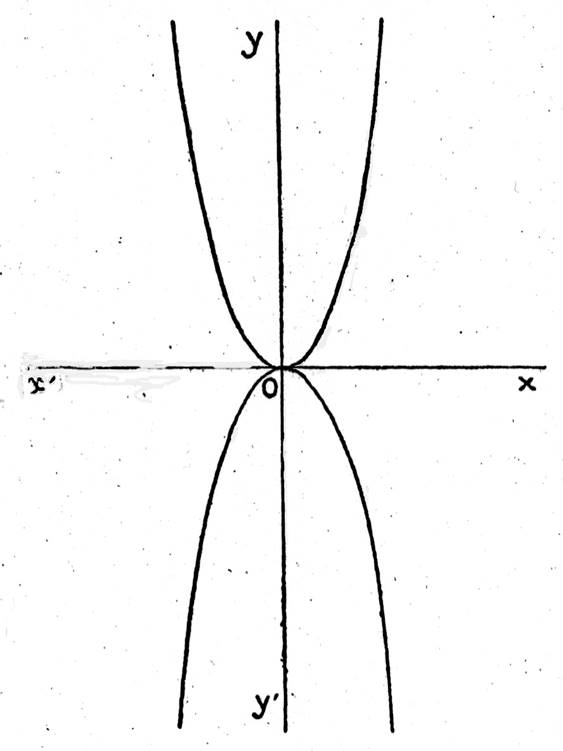
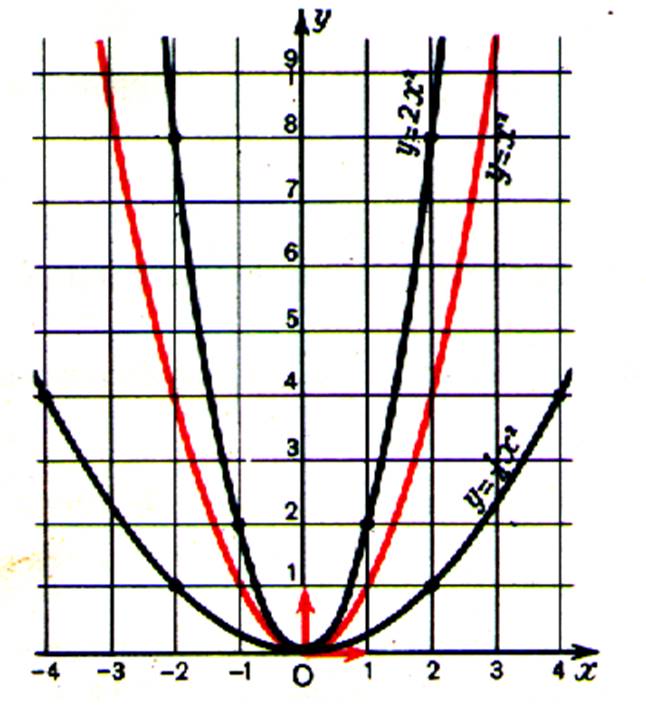
Graphique général de y = a x²

Que « x » soit positif ou négatif , « ² » sera toujours positif. Si «  » est positif, «  » pouvant être positif ou négatif , la courbe est identique à celle ci dessus, c’est à dire qu’elle se trouve au - dessus de la ligne représentant l’axe «  » Si «  » est négatif, «  » pouvant être positif ou négatif , la courbe obtenue est une parabole symétrique à la première, mais disposée au - dessous de la ligne «  ». Ici : Info plus…..

La Fonction « a x² » est une fonction dite : paire : (puissance « paire »)

Une fonction f de E vers F est dite « paire » si pour tout « x » pour lequel existe, existe également et on écrit :

Dans un repère orthonormal la représentation graphique d’une fonction paire est symétrique par rapport à l’axe des ordonnées (axe des «  »).

Exemple : la fonction de vers telle que est paire.

Sa représentation graphique est une parabole lors que l’on prendre une valeur de «  » différente de « 1 »
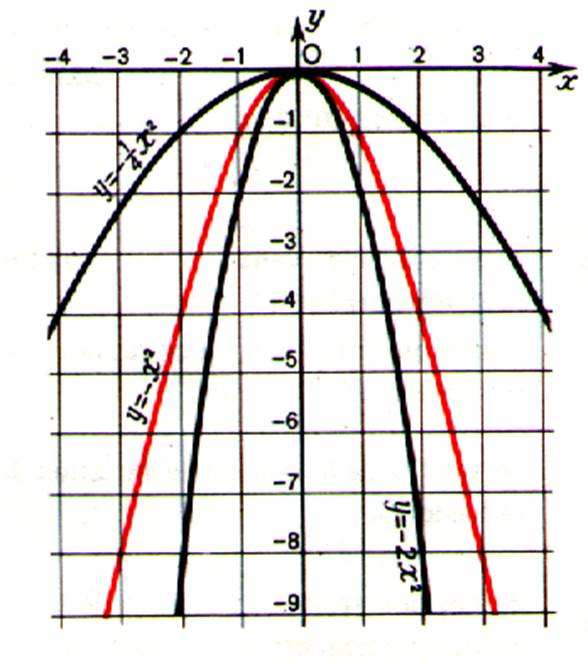
Cas a < 0	Cas : a >0

Leçon	Titre
N°	TRAVAUX d ’ AUTO - FORMATION Sur le tracé d’une parabole

TRAVAUX N° d ’ AUTO - FORMATION : CONTROLE

1°) donner la définition d’une parabole

2°) dans un repère cartésien donner l’allure d’une parabole .

3°) donner l’équation qui permet de tracer une parabole .

TRAVAUX N° d ‘ AUTO - FORMATION EVALUATION

Tracer dans un premier repère cartésien une parabole :

Exemples : ²; ou ; ²

Avec : et -