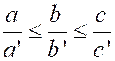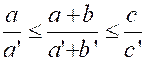·      Rappels.

·      L’ ensemble des réels ; des exemples numériques ( R )

·      Opérations sur « R »

·      Ordre sur « R »

Chapitres :

Règles de calculs

intervalle

Valeur absolue

Exercices types.

Rappels :

► N désigne l’ensemble des entiers naturels : 0 ; 1 ; 2 ; 3 ; 4 ; …..

►  Z  désigne l’ensemble des entiers relatifs : ……. ; (- 4) ;( -3) ;( -2) ; (-1) ;( 0) ; (+1) ; (+2) ;( +3) ;…….

► D  désigne l’ensemble des nombres décimaux , c’est à dire des nombres ayant un développement décimal limité.  Exemple :  0,5  Î D

► D  désigne l’ensemble des nombres décimaux relatifs : Exemples :  0,5  Î D ; (-43,371) Î D ;  ( + 23)  Î D ; (-23 ) Î D

►  Q    désigne l’ensemble des rationnels, c’est à dire des nombres de la forme :   ( ou « A » et « B »  sont des monômes ou des polynômes)

 « a » et « b » sont des nombres entiers relatifs.

a Π Z   ;   le nombre « a » est un entier relatif.

b Π Z*   ;le nombre « b » est un entier relatif différent de « zéro ».

Addition

Multiplication

Associativité

« a + ( b + c) = ( a + b) + c »

« a ( b  c ) = ( a + b) + c »

Commutativité

« a +  b ) = ( b + a )  »

«   a b = b a »

Existence d’un élément neutre

O

« a +  0 ) = ( 0 + a )= a  »

1

« 1 x a  = a x 1 = a  »

Distributivité

« ( a ( b + c  ) = ab + a c   »

En outre , dans «  Z ;   D   et   R »    tout nombre « a » possède un opposé « a’ » , tel que : «  a + a’ = 0 »

Enfin dans l’ensemble « R » tout nombre « a » non nul possède un inverse « a^-1 » tel que : « a a^-1 =  1 »

Les « R » sont les nombres Q et les autres « nouveaux »

1)     Quelques exemples de nombres réels (extérieurs à Q )

a)     Nous avons vu que  «  » ne peut être égal ni à un nombre entier , ni à une fraction ; nous savons seulement  en calculer des valeurs approchées aussi voisines que l’on veut :

        Ainsi :   1, 414213 < <1, 414214  à 0,000001 prés ( à 10^-6  prés)

  Il en est de même des racines cubiques , des racines d’indice n Î N* de nombres entiers qui ne sont pas elles – mêmes des nombres entiers.

       Ainsi : 10, 355580 <   _??????? <10, 355580   ;   à 0,000001 prés ( à 10^-6  prés)

   Ces suites décimales sont illimitées , elles ne sont pas périodiques , sinon le nombre correspondant serait rationnel .

   b)  De même  3,141592653 <  p   < 3,141592654   à 0, 000000001 prés .

b)     Les rapports trigonométries des angles tels que :

Sin 36° » 0,5878 à 0,0001  et de nombreux nombres couramment utilisé .

Tous  ces nombres sont nombres réels et appartiennent à R .

Ces nombres qui  ne sont pas « rationnels » peuvent être dits « irrationnels »

  Lorsque  la  suite de chiffres de la partie décimale  est  illimitée , si elle n’ est  pas périodique , le nombre correspondant est un irrationnel .

Ainsi pour  l’ ensemble des réels ( R )

Nous admettrons que tous les nombres peuvent s’exprimer :

-         Soit exactement par un nombre décimal ( appartenant à Z et Q )

-         Soit par les nombres ayant  une suite de chiffres  en partie décimale illimitée périodique ( donc appartenant à Q )

-         Soit par les nombres ayant  une suite de chiffres  en partie décimale illimitée  non périodique ,

Ces nombres (tous) constituent un ensemble appelé «  ensemble des nombres réels  et est désigné par la lettre « R »

La lettre « R »  désigne l’ensemble des réels, c’est à dire des nombres qui permettent de mesurer toutes les longueurs et leurs opposés.

Pratiquement tous les nombres utilisés dans les calculs élémentaires sont des nombres réels .

D’après ce qui précède  on peut écrire :

N  Ì Z Ì Q Ì R

Mais aussi N Ì Z Ì D^± Ì Q Ì R

Les réels « non  rationnels » sont dits « irrationnels »  ( voir les racines…)

·       Opérations dans R .

Info  « Cours » ++

Voir les opérations dans D^±    .Nous pouvons nous rappeler que nous pouvons définir  « Addition » ( et soustraction) , multiplication ( et division) , opérations qui possèdent les mêmes propriétés que celles données pour Q .

L’opération « puissance » est toujours définie et réciproquement l’opération d’indice « n » » est aussi définie dans  R⁺    .

·       Ordre sur « R »

Une relation d’ordre sur un ensemble « E » est une relation « R  » :

·       Réflexive :  pour tout élément « a » de « E » ;  a  R    a

·       Antisymétrique : Aucun couple  ( a ; b ) d’éléments de « E » ne vérifie simultanément les trois conditions :

( a R   b )    ;  ( b  R   a )   ; ( a  b )

·       Transitive : Si trois élément « a » ; « b » ; « c » de « E » sont tels que :  ( a R   b )    ;  ( b  R   c )   alors   ( a R   c  )

L’ensemble des « R » des nombres réels est  muni de quatre relations d’usage courants notées : 

Lire : inférieur ou égal à… ;

< 

Lire : strictement inférieur à… ;

Lire : supérieur ou égal à… ;

>

Lire : strictement supérieur à… ;

Les relations    et    sont  des relations d’ordre.

Les relation   > et <  sont antisymétriques et transitives , mais non réflexives.

Deux inégalités telles que :

« a  b »   et «  c <  d »    

Ou     « a  b »   et «  c   d »

Ou

«  a < b »  et  « c < d »

Ou     « a  b »   et «  c   d »

Sont de même sens.

Deux inégalités telles que :

« a  b »   et «  c > d » 

Ou     « a  b »   et «  c   d »

Sont  dites de sens contraires

Règles pratiques de calcul :

Info..

1°) En ajoutant ( ou en retranchant ) un même nombre aux deux membres d’une inégalité , on obtiens une inégalité de même sens ..

Exemples :

 « a  b »    entraîne  « a + c  b + c »

«  a < b »  entraîne  «  a + c  < b + c  »

Comme ajouter un réel c’est  retrancher son opposé , on peut appliquer la même règle commençant par retrancher  d’où :

 2°) En  retranchant   un même nombre aux deux membres d’une inégalité , on obtiens une inégalité de même sens .

Info..

3°) En ajoutant « membre à membre »  deux inégalités de même sens , on obtient  une inégalité de même sens .

Exemple : « a  b »   et  « c  d »   entraînent  « a + c   b + d  »

Attention !!!   Il n’est pas permis de retrancher des inégalités :  «  19    17  »  et  «  13    3  », il n’est pas possible de déduire : 19  - 13   17  - 3

4°) En multipliant les deux membres d’une inégalité par un même réel non nul , on obtient une inégalité :

·       De même sens  si le multiplicateur est positif.

·       De sens contraire si le multiplicateur est négatif.

Info.

Intervalles :

« a » et « b »étant deux réels tels que « a  b » 

est l’ensemble des réels « x » tels que

[ a , b ]

« a  x  b »

[  a , b [

« a  x <  b »

] a , b ]

« a  < x  b »

] a , b [

« a  < x <  b »

] a , +  [

« a   <  x  »

[ a , +  [

« a  x  »

] -  , b [

« x <  b »

] -  , b ]

« x  b »

Info

Valeurs absolues :

 est celui des deux réels « + x » et « -x » qui est positif.

 = 0

·       La valeur absolue d’une somme est inférieure ou égale à la somme des valeurs absolues :   +

·       La valeur absolue d’un produit est égale au produit des valeurs absolues.  =   

Fin des rappels  :

Exercices types :

1.     

Nier l’inégalité suivante :  a  -5

2.     

Nier l’inégalité suivante :  b   2

3.     

Nier l’inégalité suivante :   c < 0

4.     

Nier l’inégalité suivante :  0   d  < 1

5.     

Nier l’inégalité suivante :  - 1    f  < - 0,5

6.     

Nier l’inégalité suivante :  f < - 2     ou   f > 3

7.     

Vérifier que le réel :  [  ( a + b ) -  ]  est égal au plus petit des deux réels « a » et « b »

8.      

En remarquant que les radicandes sont des carrés parfaits , simplifier les écritures suivantes (dont on discutera selon les valeurs de « a » :

9.      

En remarquant que les radicandes sont des carrés parfaits , simplifier les écritures suivantes (dont on discutera selon les valeurs de « a » :

10.  

En remarquant que les radicandes sont des carrés parfaits , simplifier les écritures suivantes (dont on discutera selon les valeurs de « a » :

11.  

En remarquant que les radicandes sont des carrés parfaits , simplifier les écritures suivantes (dont on discutera selon les valeurs de « a » :

12.  

En remarquant que les radicandes sont des carrés parfaits , simplifier les écritures suivantes (dont on discutera selon les valeurs de « a » :

13.  

Soit « a » un nombre réel.

Sachant que «  a  < -1 », que peut -on dire de « a² » , de « -a » et de «  » ?

14.  

Soit « a » un nombre réel.

Sachant que «  a  > 5 », que peut -on dire de « a² » , de « -a » et de «  » ?

15.  

Soit « a » et « b » deux réels . On sait que :  4 < a < 7   et   3 <  b < 4   que peut-on dire de « a – b » ?

16.  

Soit « a » et « b » deux réels . On sait que :  - 1  < a < 3    et   -2 <  b < 0   que peut-on dire de « a – b » ?

17.  

Soit « a » et « b » deux réels . On sait que :  -2    a  2    et   - 2   b  2   que peut-on dire de « a – b » ?

Quelles  inégalités     vérifie t-il si le réel « a » vérifie :

18.  

  - 3 < a < 3   ?

19.  

  - 1  a  1 ?

20.  

  - 2 < a < 0 ; ? 

21.  

  - 2 < a  < 4 ; ?

22.  

  - 2  a < 2 ; ?

23.  

  - 2 <  a 3 ; ?

24.  

- 5 < a  - 3 ; ? 

Quelles inégalités le réel « a » vérifie-t-il sachant que

25.  

      < 2               

26.  

        3  

27.  

        > 1

28.  

     1

29.  

   < 2  

Déterminer l’intersection des intervalles « A » et « B » donnés.

30.  

A = [ 0 ; 4  ]   ;   B =  [ 2 ; 6  ]

31.  

A = [ 0 ; 5  ]   ;   B =  [ 5 ; 6  ]

32.  

A = [ 0 ; 3   [   ;   B =  [ 2 ; 4   [

33.  

A = [ - 1  ; 4 [   ;   B =  [ 3  ; 4 [

La réunion de deux intervalles « A » et « B » donnés est-elle un intervalle ? Si oui , préciser cet intervalle.

34.  

A = [ 1 ; 4  ]   ;   B =  [ 2 ; 5  ]

35.  

A = [ 1 ; 2  ]   ;   B =  [ 2 ; 3  ]

36.  

A = [ -1  ; 0 [  ;   B =  [ 0 ; 2  ]

37.  

A = [ -1  ; 1 [  ;   B =  ]  1 ; 3  [

38.  

On donne deux réels « a » et « b » . On sait que :  4,5 < a < 4,6       et      5,3   b  5,4

Que peut –on en déduire pour «  a + b » , pour «  a – b »  , pour     ; pour  «  a² + b² »         

39.  

Comparer les nombres  et   +  : on déterminera leur ordre et on donnera un majorant  de leur écart .

40.  

On donne quatre réels « a » , « b » , « c » et « d » tels que :   a < b    et c < d

Démontrer l’ inégalité : «  a – b < d –c  »

41.  

On donne quatre réels « a » , « b » , « c » et « d » tels que :   a < b    et c < d

Démontrer l’ inégalité :     «  a – d < b – c  »

42.  

On donne six  réels « a » , « b » , « c » et   « a’ » , « b ‘ » , « c’ » tels que :

Etablir les inégalités : «  a b’     b a’            et       

43.  

44.  

45.  

46.