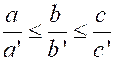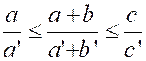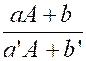|
|
|
|
|
|
|
|
TITRE : EXERCICES sur les
inégalités L’ensemble des nombres Réels
|
|
|
|
|
|
Exercices types : |
|
|
1.
|
Nier l’inégalité suivante : a |
|
|
2.
|
Nier l’inégalité suivante : b
|
|
|
3.
|
Nier l’inégalité suivante : c < 0 |
|
|
4.
|
Nier l’inégalité suivante : 0
|
|
|
5.
|
Nier
l’inégalité suivante :
- 1 |
|
|
6.
|
Nier l’inégalité suivante : f < - 2 ou
f > 3 |
|
|
|
|
|
|
7.
|
Vérifier que le réel : |
|
|
8.
|
En remarquant que les radicandes sont des carrés parfaits , simplifier les écritures suivantes (dont on
discutera selon les valeurs de « a » :
|
|
|
9.
|
En remarquant que les radicandes sont des carrés parfaits , simplifier les écritures suivantes (dont on
discutera selon les valeurs de « a » :
|
|
|
10. |
En remarquant que les radicandes sont des carrés parfaits , simplifier les écritures suivantes (dont on
discutera selon les valeurs de « a » :
|
|
|
11. |
En remarquant que les radicandes sont des carrés parfaits , simplifier les écritures suivantes (dont on
discutera selon les valeurs de « a » :
|
|
|
12. |
En remarquant que les radicandes sont des carrés parfaits , simplifier les écritures suivantes (dont on
discutera selon les valeurs de « a » :
|
|
|
13. |
Soit « a » un nombre réel. Sachant que « a < -1 », que peut
-on dire de « a² » , de « -a » et de « |
|
|
14. |
Soit « a » un nombre réel. Sachant que « a > 5 », que peut -on
dire de « a² » , de « -a » et de « |
|
|
15. |
Soit « a » et « b » deux réels . On sait que : 4 < a < 7 et
3 < b < 4 que peut-on dire de « a –
b » ? |
|
|
16. |
Soit « a » et « b » deux réels . On sait que : - 1
< a < 3 et -2 <
b < 0 que peut-on dire de
« a – b » ? |
|
|
17. |
Soit « a » et « b » deux réels . On sait que : -2
|
|
|
|
Quelles
inégalités |
|
|
18. |
- 3 <
a < 3 ? |
|
|
19. |
- 1 |
|
|
20. |
- 2 <
a < 0 ; ? |
|
|
21. |
- 2 <
a < 4 ; ?
|
|
|
22. |
- 2 |
|
|
23. |
- 2
< a |
|
|
24. |
- 5 < a |
|
|
|
Quelles inégalités le réel « a »
vérifie-t-il sachant que |
|
|
25. |
|
|
|
26. |
|
|
|
27. |
|
|
|
28. |
|
|
|
29. |
|
|
|
|
|
|
|
|
Déterminer l’intersection des intervalles
« A » et « B » donnés. |
|
|
30. |
A = [ 0 ; 4
] ;
B = [ 2 ; 6 ] |
|
|
31. |
A = [ 0 ; 5
] ;
B = [ 5 ; 6 ] |
|
|
32. |
A = [ 0 ; 3
[ ;
B = [ 2 ; 4 [ |
|
|
33. |
A = [ - 1
; 4 [ ; B =
[ 3 ; 4 [ |
|
|
|
|
|
|
|
La réunion de deux intervalles « A » et
« B » donnés est-elle un intervalle ? Si oui
, préciser cet intervalle. |
|
|
34. |
A = [ 1 ; 4
] ;
B = [ 2 ; 5 ] |
|
|
35. |
A = [ 1 ; 2
] ;
B = [ 2 ; 3 ] |
|
|
36. |
A = [ -1 ;
0 [ ; B =
[ 0 ; 2 ] |
|
|
37. |
A = [ -1 ;
1 [ ; B =
] 1 ; 3 [ |
|
|
|
|
|
|
38. |
On donne deux réels « a » et
« b » . On sait que : 4,5 < a <
4,6 et 5,3 Que peut –on en déduire pour « a + b » , pour « a – b » , pour
|
|
|
39. |
Comparer les nombres |
|
|
40. |
On donne quatre réels « a » , « b » , « c » et « d »
tels que : a < b et c < d Démontrer l’ inégalité :
« a – b < d –c » |
|
|
41. |
On donne quatre réels « a » , « b » , « c » et « d »
tels que : a < b et c < d Démontrer l’ inégalité : « a – d < b – c » |
|
|
42. |
On donne six
réels « a » , « b » ,
« c » et « a’ » ,
« b ‘ » , « c’ » tels que : Etablir les inégalités : « a b’ |
|
|
43. |
Rappel : « définition : rationnel » On donne quatre nombres pour former des rationnels « a » , « b » , « a’ » et « b’ » avec « a’ |
|
|
44. |
Soit « a » et « b » deux
rationnels positifs . Montrer que si |
|
|
|
|
|
|
|
|
|
TRAVAUX AUTO FORMATIFS.
1°) Nommer
les ensembles définis par les lettres : N ; Z ; D ; Q (accompagner la réponse par un exemple)
2°) Que
désigne la lettre « R » :
3°) Citez
des nombres irrationnels.
1°) Classer avec la
relation £ les trois nombres ; ; et p
En déduire le classement par la même relation de ; ; et p
(pour résoudre cette question
déterminer des valeurs approchées décimales des deux fractions avec un nombre
de chiffres décimaux suffisant.)
2°) Les valeurs approchées par défaut d’un nombre sont successivement : 1 ; 1,1 ;
1,12 ; 1,12123 ; 1,121231234, etc . ;les chiffres décimaux successifs constituant une suite de plus en plus longue
des nombres entiers .Le nombre est-il rationnel ? est-il
réel ?
3°) Pourquoi la valeur de x
tel que x2 = 5 , est-elle extérieure à
l’ensemble Q . Montrer que dans l’intervalle
[2 ; 3 ]
cette valeur constitue une coupure pour les nombres de l’ensemble Q. En
est-il de même pour x2 = 6,25 ?
CONTROLE : corrigé :
1°) Nommer les ensembles définis par les
lettres : N ;
Z ; D ; Q (accompagner la
réponse par un exemple)
► N
désigne l’ensemble des entiers naturels : 0 ; 1 ; 2 ;
3 ; 4 ; …..
►
Z désigne l’ensemble des entiers
relatifs : ……. ; (- 4) ;( -3) ;(
-2) ; (-1) ;( 0) ; (+1) ; (+2) ;( +3) ;…….
► D désigne l’ensemble des nombres décimaux , c’est à dire des nombres ayant un développement
décimal limité.
Exemples : 0,5
Î D ; (-43,371) Î D ; ( + 23)
Î D ; (-23 ) Î D
►
Q désigne l’ensemble des rationnels, c’est à dire des nombres de
la forme :
2°) Que désigne
la lettre « R » :
l’ensemble des
nombres réels.
3°) Citez des nombres irrationnels.
Pi ; racine carré de 2 ; racine
carrée de 3 ; racine carrée de 7 ;…
EVALUATION:
1°) Classer avec la relation £ les trois nombres ; ; et p
En déduire le classement par la même
relation de ; ;
et p
(pour résoudre
cette question déterminer des valeurs approchées décimales des deux fractions
avec un nombre de chiffres décimaux suffisant.)
2°)
Les
valeurs approchées par
défaut d’un nombre sont successivement : 1 ; 1,1 ;
1,12 ; 1,12123 ; 1,121231234, etc . ;les chiffres décimaux successifs constituant une suite de plus en plus longue
des nombres entiers .Le nombre est-il rationnel ? est-il
réel ?
3°) Pourquoi la valeur
de x tel que x2 = 5 , est-elle
extérieure à l’ensemble Q . Montrer que dans l’intervalle [2 ; 3 ] cette valeur constitue une coupure pour les
nombres de l’ensemble Q. En est-il de même pour x2 = 6,25 ?