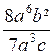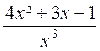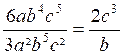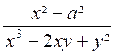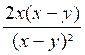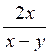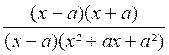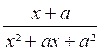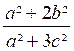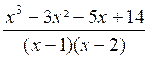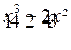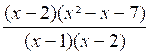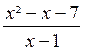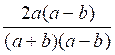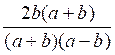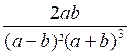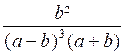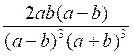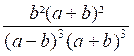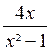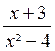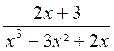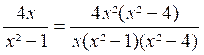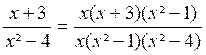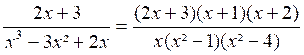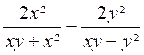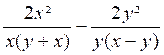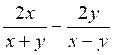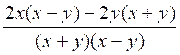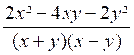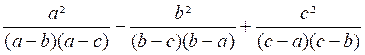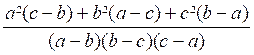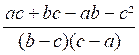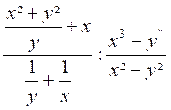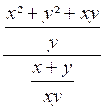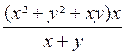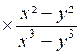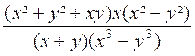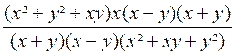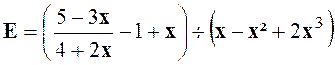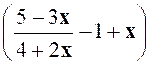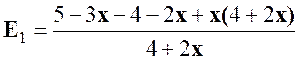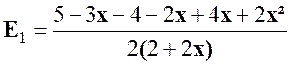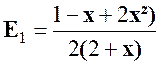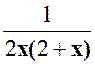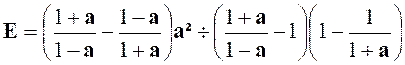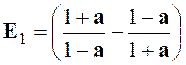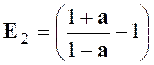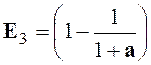|
|
|
|
|
|
|
|
ENVIRONNEMENT du dossier:
|
CHAPITRES :
|
@ info+ |
Les FRACTIONS dites « RATIONNELLES » : |
@ info+ |
|
|
|
|
|||||
|
|
1.
Définition ;, |
|
|||||
|
|
2.
Simplification |
|
|||||
|
|
|
||||||
|
|
|
|
|||||
|
|
|||||||
|
TEST |
COURS |
Interdisciplinarité
|
|
||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
Définition.
On appelle « fraction rationnelle » le quotient de deux monômes ou
polynômes. Exemples : Le dividende est le numérateur de la fraction, le
diviseur est son dénominateur ;le numérateur et
le dénominateur en sont les deux termes. |
|
||||||||||||
|
SIMPLIFICATION. |
|
|||||||||||||
|
|
Le premier problème qui se pose est évidemment
d’écrire une fraction rationnelle sous la forme la plus simple, c’est à dire
de la simplifier. Une fraction rationnelle sera d’autant plus
simple que ses deux termes seront de plus petit degré. De même que pour une
fraction numérique, pour simplifier une fraction rationnelle, on divisera
ses deux termes par un même facteur. Pour cela , on essaiera
de mettre ses deux termes sous forme de « produits de facteurs ».
On pourra alors simplifier la fraction s’il y a au numérateur et au
dénominateur un facteur commun. Exemples :
REMARQUE 1 : Il faut bien faire attention de ne pas supprimer
un même terme au numérateur et au dénominateur si ceux-ci n’ont pas été mis
sous forme de produits. Par exemple : il ne faut pas écrire : en supprimant « a² » aux termes car, en
procédant ainsi, on retranche « a² » aux deux termes et on
n’obtient pas une fraction équivalente. ( pour
vérifier qu’il n’y a pas égalité donner par exemple à « a =
+2» et « b= + 3» il suffit
ensuite de faire le calcul. Dans chaque membre) REMARQUE 2 : Il arrive fréquemment qu’on
peut mettre immédiatement un des termes d’une fraction sous la forme d’un
produit de facteurs du premier degré de la forme (x -a ) ( x - ³ ) ……. Il est alors naturel de se demander s’il est
possible de mettre en facteur dans l’autre terme l’un des binômes (x -a ) ( x - ³ ) ……. * Soit par exemple la fraction : A = Examinons si dans le numérateur « N »
on peut mettre « x- 1 » en
facteur, c’est à dire s’il existe un polynôme « N’ » tel que l’on
ait quel que soit « x » : N
= ( x - 1) N’ S’il en est ainsi, pour « (x - 1 ) N’ = 0 »
donc « N = 0 » Or pour « x = 1 ; N = 1 - 3 - 5 +14 ;
donc dans « N » on ne peut certainement pas mettre
« x-1 » en facteur. Voyons de même si dans « N » il est
possible de mettre « x-2 » en facteur. Le même raisonnement que précédemment nous prouve
que pour qu’il en soit ainsi il faut que « N » s ‘ annule pour
« x = 2 » Pour « x = 2 » ,
on a « N = 8 - 12 -10 +14 =
0 » donc dans « N » on peut peut - être
mettre « x - 2 » en facteur. Pour voir si cela est effectivement possible , nous allons essayer de mettre
« N » sous la forme d’une
somme de binômes dans lesquels on peut mettre « x-2 » en facteur . Avec le
premier terme « x3 » il faudrait «
-2x² » ; on aurait ainsi « x 3 - 2 x² = x²
( x - 2) » Comme dans « N » on a
« -3x² » (
et non pas « -2x²) il faut
ajouter « -x² » Avec
« -x² » il faudrait « 2x » ,
on aurait ainsi : - x² + 2x = - x ( x - 2) Comme dans « N » on a « -5x »
(et non pas « 2x ») il faut ajouter « -7 x » Finalement il reste donc - 7 x + 14 = - 7 ( x -2) Les calculs précédents se résument ainsi :
= ( x - 2 ) ( x² -
x - 7 ) Nous
pouvons donc simplifier la fraction « A » et
écrire : A = |
|
||||||||||||
|
|
||||||||||||||
|
|
On peut prendre pour dénominateur commun le
produit des dénominateurs. Soient par exemple les deux fractions :
La 1ère est équivalente à Il est souvent possible de trouver un
dénominateur commun plus simple que le produit des dénominateurs. Pour
qu’une expression puisse être
prise comme dénominateur commun, il suffit qu’elle contienne en facteur
chacun des dénominateurs des différentes fractions. On pourra former le dénominateur commun en
utilisant une règle analogue à celle
utilisée pour les fractions numériques : ( @ info) On
décompose les dénominateurs eu produits de facteurs et on fait le produit de
tous les facteurs , communs ou non communs , chacun d’eux étant pris avec son
plus fort exposant . EXEMPLE 1
: Réduire au même dénominateur :
On pourra prendre comme dénominateur commun ( a + b ) 3
( a - b )3 Les deux fractions données sont équivalentes à :
EXEMPLE 2 :
Réduire au même dénominateur :
Mettons les dénominateurs sous forme de produits . x² - 1 = ( x +1) ( x -
1)
x² - 4 = ( x
+2) ( x - 2) x3 - 3 x² + 2x = x ( x²
- 3x +2 ) Regardons si dans le trinôme « x² - 3x +
2 » on peut mettre en facteur l’un des facteurs des deux premiers
dénominateurs. Pour
« x = 1 » ; on a
x² - 3x + 2 = 1 - 3 + 2 = 0 Donc , dans ce trinôme il est peut-être possible de mettre « x-1 »
en facteur. En procédant comme nous l’avons vu pour A =
x² - 3 x + 2 = x² -x - 2x +2 = x ( x-1) - 2 ( x
-1) = ( x - 1 ) ( x - 2 ) Donc x3
- 3 x² + 2x = x ( x - 1) ( x - 2) Finalement, on prendra pour dénominateur commun « x (x-1)(x+1)(x-2)=
x ( x²-1) ( x² - 4) et les fractions données sont respectivement équivalentes à :
|
|
||||||||||||
|
OPERATIONS
. |
|
|||||||||||||
|
|
Les opérations sur les fractions rationnelles se
font en appliquant les mêmes règles que pour les fractions numériques. Exemple 1 Calculer
l’expression : A = Les deux fractions se simplifient et on a : A
= = = = |
|
||||||||||||
|
|
Exemple2 : Calculer l’expression :
A = Nous prendrons pour dénominateur commun : ( a
- b) ( b - c) (c - a) A = Regardons si le résultat obtenu peut se
simplifier. Pour voir si dans le numérateur « N » on peur mettre « a -b » en facteur
, remplaçons « a » par « b » ; on
obtient : * b ² ( c -b) + b² ( b- c) + c² × 0 = 0 Dons dans « N » on peut « peut
être » mettre « a - b » en facteur .On a : N = a² c - a²b + b² a - b² c - c² ( a -b) =
c( a² - b² ) - a b ( a - b) - c² ( a - b) = c ( a- b)
( a + b )- a b ( a - b ) - c² ( a - b) = ( a - b) ( ac + b c - a b - c² ) Donc
A = Pour b = c , le numérateur « N’ » s’annule . Il est donc , peut -
être possible de mettre « b -c » en facteur dans
« N’ ».On a : N’ = a ( c - b ) + c ( b - c) = ( b - c ) ( c - a) Finalement A = 1 |
|
||||||||||||
|
|
Exemple 3 . Calculer
l’expression : A
= La 1ère fraction est égale à : Donc A
=
=
=
A = x |
|
||||||||||||
|
|
« Rationnelles » : les expressions
algébriques quelconques et simplification. |
|
||||||||||||
|
|
Quelque soit le degré de complication apparente d’une expression algébrique,
on arrivera à lui donner une forme plus simple, à la condition d’être méthodique , de n’opérer les transformations successives
que sur des fragments de l’expression proposée, fragment mais aussi peu
importants que l’on voudra. |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
Exercice 1 : Transformer l’expression : |
|
||||||||||||
|
|
Solution :
Nous nous occupons de E1 =
Occupons nous de E 2 = x – x ² + 2 x 3 =
x ( 1- x ² + 2 x ² ) Nous savons que qui est de la forme « E =
Simplifions par
( 1- x ² + 2 x ² ) qui n’est jamais nul ( à voir plus tard) E = |
|
||||||||||||
|
|
Exercice 2 : Transformer l’expression : |
|
||||||||||||
|
|
Indications :
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
Travaux auto formatifs. |
|
||||||||||||
|
|
DEVOIR : Voir chapitre par chapitre. |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
Pour chaque chapitre ,
et pour approfondir cliquer sur « @ info » |
|
||||||||||||
|
|
EVALUATION |
|
||||||||||||
|
|
Pour chaque chapitre, et pour approfondir cliquer
sur « @ info » |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|