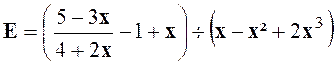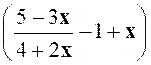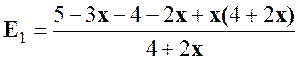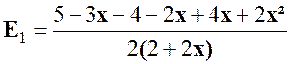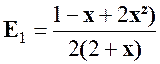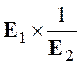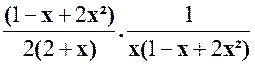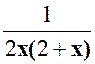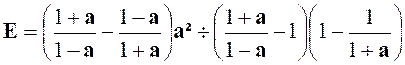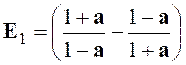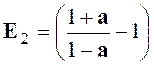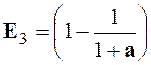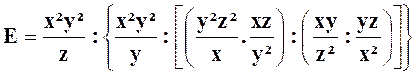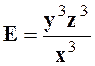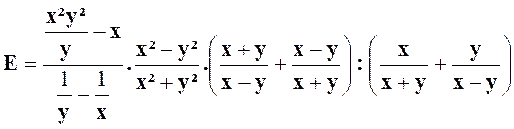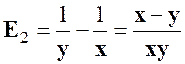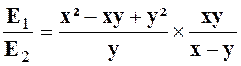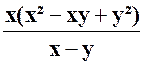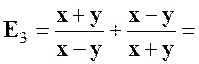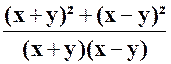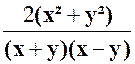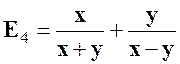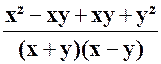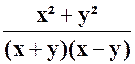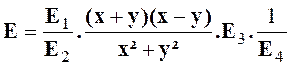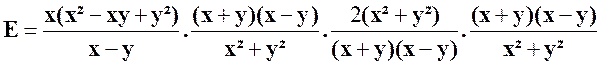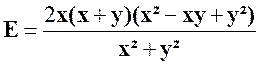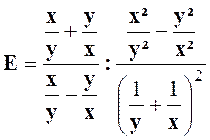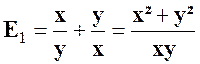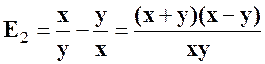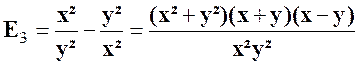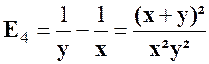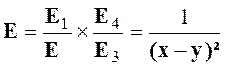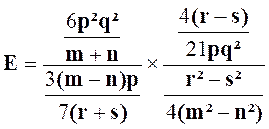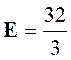@ info+

Les « RATIONNELLES » :

@ info+

               Quelque soit le degré de complication apparente d’une expression algébrique, on arrivera à lui donner une forme plus simple, à la condition d’être méthodique , de n’opérer les transformations successives que sur des fragments de l’expression proposée, fragment mais aussi peu importants que l’on voudra.

Exercice 1 : Transformer l’expression :

        qui est de la forme  «  »

Solution : 

Nous nous occupons de  E₁  =   =  Réduisons tous les termes   au même dénominateur « 4 + 2x »

            ,   ;

Occupons nous de   E ₂  = x – x ² + 2 x ³   =   x ( 1- x ² + 2 x ² )     

Nous savons que qui est de la forme  « E =   » s’écrit :  E =    =   . 

Simplifions par   ( 1- x ² + 2 x ² )  qui n’est jamais nul ( à voir plus tard)

E =         avec :   x 0  et   x -2

Exercice 2 : Transformer l’expression :

Indications :

ensuite on applique :   E =  E ₁ a² : E ₂.E₃ =  2a ;           avec   a +1     et   a -1 ; et     a 0 

Exercice 3 : Transformer l’expression :

réponse :                     avec   x 0      et   y  0 ; et     z 0 

Comme métaphore :  En somme on procède comme un mécanicien ajusteur  qui prépare  les divers éléments d’un  ensemble de pièces  et qui procède au « montage » uniquement lorsque les pièces sont bien préparées.

Exercice 4 : Transformer l’expression :

solution :   Prenons :

Et formons tout de suite :

 =          avec   x 0      et   y  0 

Calculons  ensuite :

= 

 = = 

dés lors :  

ou :

et simplifions :

Réponse :                           avec   x  +y      ;    x  - y  ; et     y 0 

Exercice 5 : Transformer l’expression :

Indications :

Réponse :

                                                              avec   x  0      ;    y  0  ; et    x + y 0   et x + y 0 ;x - y 0 

Exercice 6 : Transformer l’expression :

Réponse :

r  + s    et    r - s

m  + n  et    m  - n ;  

p   0

q   0

Travaux auto formatifs.

DEVOIR : donner en  exercices  les exemples

CONTROLE :

Pour chaque chapitre , et pour approfondir cliquer sur « @ info »

EVALUATION

Savoir refaire les exemples