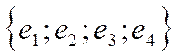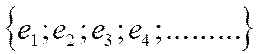|
|
|
Pré requis:
|
Définitions : les chiffres et
nombres |
|
Objectif
précédent : Notions simples
sur les ensembles |
Objectif suivant : |
DOSSIER:
LES « « ENSEMBLES » de NOMBRES
(présentation ; généralités)
LECTURE : « L’ Infini »
mathématique.
A ) LES ENSEMBLES. (définition ;
désignation ;définition d’un élément ;les principaux ensembles de
nombres).
B) ECRITURE symbolique
mathématique D' UN ENSEMBLE.( dit en extension).
C ) Approches sur « LES SUITES » ou Progressions de
nombres .
|
|
|
||||||
|
|
|
Devoir n°1 (première
approche) |
|
|
|
|
|
|
|
LECTURE : « L’ Infini »
mathématique |
|
Au cours de notre étude des
fonctions,nous emploierons souvent les expressions :
« l’infiniment grand» ;
« l’infiniment petit »
, ou de façon abrégée « l’infini »
Que signifie ces mots ?
Tout d’abord il est clair qu’on peut toujours augmenter un nombre donné,
allonger une droite donnée. Considérons donc une grandeur
et faisons croître sa valeur absolue , de telle façon qu’elle soit toujours supérieure à
une quantité qu’on pourra nous assigner
, aussi grande soit telle. Nous appellerons cette valeur, « numériquement
indéfinissable » , l’infiniment grand et nous la
représenterons par le symbole : ∞ .
De même nous définirons « l’infiniment petit » comme une
grandeur décroissante , inférieure en valeur absolue à
toute quantité donnée aussi petite soit elle et nous la représenterons par le
symbole : 
. ( lettre grecque appelée « epsilon ») ;Il est à
noter que l’infiniment grand et l’infiniment petit peuvent être positifs ou
négatifs.
±
. ; ± .
Ainsi que l’ a remarqué Pascal, l’infiniment
grand et l’infiniment petit sont intimement liés l’un à l’autre .
Considérons, par exemple, la fonction 
en même temps que son dénominateur devient infiniment petit
, cette fraction devient « infiniment grande » ,
inversement elle
est infiniment petite lorsque « x » est
infiniment grand.
Cette corrélation a d’ailleurs
une conséquence remarquable.
Si l’on donne a « x » deux valeurs infiniment petites , l’une
négative - e , l’autre positive + e ,
et il est évident que ces deux valeurs sont aussi voisines qu’on le veut , y
devient successivement infiniment grande et négative ; -
z. , puis infiniment grande et
positive ; + z. en sorte que ces
deux valeurs indéfinis se succèdent immédiatement, sans valeurs intermédiaires
|
|
COURS |
|
La théorie des
ensembles a été inventée par Georg Cantor, mathématicien allemand (1845 - 1918)
|
A ) LES ENSEMBLES. |
|
1°) Définition:
Un ensemble est une collection
d'objets distincts ayant un caractère commun et bien défini.
Exemples :des pins ;des crayons , les élèves
d’une même classe ;.................
Mais aussi : l’ensemble des
points d’une droite , l’ensemble des voyelles , l’ensemble
des couleurs de l’arc - en - ciel , ……
En mathématique :il existe les ensembles de nombres et les ensembles
géométriques. : des nombres entiers naturels ,les nombres
décimaux; des vecteurs....,
2°) DESIGNATION
D'UN ENSEMBLE:
On désigne généralement un ensemble par une lettre majuscule. « A », « B » , « S »,….
Remarque : il y a des conventions internationales pour désigner
certains ensembles tels les lettres qui désignent les ensembles de
nombres : N , D , Q , R ,….
3°) ELEMENT (définition) :
Chacun des « objets » de l’ensemble est appelé « un
élément » de cet ensemble.
Quelques informations sur les principaux "Ensembles" de nombres
Il existe 2 grandes
catégories de nombres :
-
les
nombres non relatifs (on considère qu 'ils sont "positifs" , ils ne sont pas
précédés par un signe + ) ;
-
et les nombres relatifs (ils sont
"positifs" (le
signe + l'indique) ou ils sont
négatifs (le signe - l'indique)
4°) LISTE DES
PRINCIPAUX ENSEMBLES DE NOMBRES en mathématiques :
|
Lettres couramment
utilisées pour désigner des « ensembles de nombres » |
|
|
Notions :nombres entiers naturels |
N : représente l'ensemble des nombres entiers naturels
Exemples :
3 ; 4 ; 5 ; 267 ; 2567 ; (classés par
ordre croissant : voir objectif n°..........) |
|
Z (+
ou -) Notions : nombres entiers positifs ou négatifs . |
Z +ou- : représente l'ensemble des nombres entiers relatifs. Exemples : pour Z+
(+5) ; (+63) ; (+125 ) ; (+ 5678
) ;
pour Z- (-5) ;(-89) ;
(-564) ; (- 781 ) ;(-1536) |
|
D |
D : représente l'ensemble des nombres décimaux "non - relatifs" exemples : 0,01 ; 2,50 ; 5,87 ;126,78 (voir système décimal) |
|
D +ou- : représente l'ensemble des nombres décimaux relatifs Exemples de D+ =
(+0.23) ; (+5,89 ) ; (+89,56) ;
.............(classés par ordre croissant : Exemples de D- =
(- 0.23) ; (-5,89 ) ; (-89,56) ; .............(classés par ordre
décroissant ; |
|
|
Q |
Q : ensemble des nombres dits
« rationnels » il contient en plus des D des
nombres représentés par les fractions et les rationnels |
|
R : représente l ’ ensemble
des nombres réels : dont fait
parti le nombre π
( dire « pi » )et « les valeurs de certaines racines » L’ensemble de tous
les nombres : entiers , décimaux , rationnels et irrationnels est l’ensemble des réels . Exemples : π ; 1/3 ; -1,2 ; |
|
|
« * »
l’étoile signifie que la valeur « zéro » est exclue de l’ensemble
des nombres réels. |
|
|
R+ |
On ne considère
que l’ensemble des nombres réels positifs |
|
R- |
On ne considère
que l’ensemble des nombres réels négatifs |
|
S |
S est souvent utilisé pour désigner des
"suites" (les principales
sont : les suites arithmétiques ,suites géométriques ;suites logarithmiques ) |
|
U |
Comme pour "S" , "U"
est souvent utilisé pour désigner des "suites de nombres"
.géométriques , arithmétique . |
;
;
B) ECRITURE symbolique
mathématique D'UN ENSEMBLE.( dit en extension)
Il existe des ensembles, dit "finis" et des ensembles "non
finis" dit "infinis".
A) Ecriture symbolique mathématique
d'un ensemble "fini" . (un ensemble est dit
« fini »si on connaît tous les
éléments)
Procédure:
Après avoir nommé
l'ensemble par une lettre majuscule suivi du signe = ,on
énumère tous les éléments de l'ensemble en les séparant par une virgule (par un
point - virgule pour des nombres)et encadrés par des accolades:
Le modèle
mathématique est :
exemple : E = 
traduction
littérale : E est le nom de l’ensemble , il contient 4 éléments
« e ».c’est un ensemble fini
puisque après le quatrième éléments il n ’ y a pas de points de
suspension.
EXEMPLE d ’ application :
Les diviseurs (D ) de 24 s'écrit en extension:
D 24 = 
1;2;3;4;6;8;12;24
B)Ecriture symbolique mathématique d'un ensemble
"infini". On nomme l'ensemble "infini"
,lorsque l'on ne peut pas nommer tous les éléments.
écriture mathématique , d ‘un
"ensemble infini" : (deux façons)
E = 
ou E = 
Procédure:
On écrit que les premiers
éléments et l’on complète par des points de suspensions, le tout encadré par
des accolades.
Exemples
numériques :
-
soit l'ensemble des nombres entiers naturels qui se note : N
en écriture mathématique cela donne :
N = 0;1;2;3 ;....
-
soit l'ensemble des nombres entiers relatifs qui se note : Z
en écriture mathématique cela donne :
Z = …… ; ( -2) ; ( -1) ; 0; (+1); (+2) ;..
-
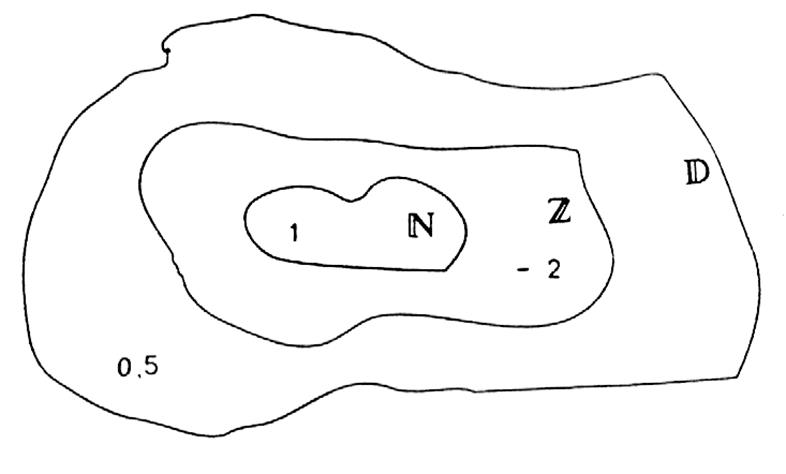
soit l'ensemble des nombres décimaux
qui se note : D
en écriture mathématique cela donne :
D = 0 ; 0,5;
1 ; 1,2;..
Ces ensembles
peuvent se représenter graphiquement par
le « diagramme de Venn »)
- l'ensemble des nombres décimaux relatifs qui se note : D± ( dans lequel se
trouve « D »)
en écriture mathématique cela donne : D± = …. ; ( -2) ;
(-1,5) ; 0,5; 1,2;..
C ) Progressions : "Suite" : de nombres : (info +
sur : Les progressions
arithmétique et géométriques.)
Une suite est un ensemble d'éléments connus
"en compréhension".
Une
"suite" est un ensemble
d ' éléments (de nombres) dont les éléments ont une propriété caractéristique
permettant de les reconnaître (identifier) ;
Pour savoir si un élément "x" appartient
à une suite ,il faut se demander si l 'objet "x" possède ou non cette
propriété ; il est alors connu en compréhension.
L'ordre des éléments est important ( croissant ou décroissant) ; ils
sont ou peuvent être "indicés"
( l'indice indique le numéro d'ordre ou
de rangement de ces éléments)
« suites de
nombres » :
On utilise fréquemment des suites de
nombres rangés dans un ordre déterminé.
Exemples :
Suite 1 : suite des nombres entiers
naturels : 1 ; 2 ;
3 ; 4 ; 5 ; 6 ; 7 ; …… ; n ;…
Suite 2 : la suite des ouverture de
diaphragme d’un appareil
photographique :
2
; 2 ,8 ;
4 ; 5,6 ; 8 ; 11 ; 16 ; 22
Suites des avances longitudinales et transversales , en mètres par minute , sur une
fraiseuse :
Suite 3 : 9 ; 11 ; 14 ; 18 ;
23 ; 29 ; 36 ; 45 ; 58
Suite 4 : 69 ; 86 ; 110 ; 137 ;
173 ; 220 275 ; 346 ; 440
Chacun des nombres figurant dans une
suite est un « terme » de cette suite.
Certaines suites comportent un nombre
fini de termes ( comme la suite 2 qui comprend 8
termes) . Ce sont des suites finies.
D’autres comportent une infinité de termes , ce sont des suites infinies ou illimités ( par exemple : la suite 1)
Notation :
On représente en général les termes
d’une suite par une même lettre , chaque terme étant
repéré par un indice correspondant au rang qu’il occupe dans la suite.
Ainsi pour la suite 2 :
U1 = 2
; u2 = 2,8 ; u3 = 22
Il existe des suites dont les termes
successifs apparaissent au hasard. Mais , le plus
souvent , on définit une suite à l’aide
d’une loi de formation permettant :
-
soit de calculer chaque terme en fonction de son rang : un = f ( n)
Ex : suite des nombres
entiers : un = n
Suite des nombres pairs :
un = 2 n
-
Soit , lorsqu’on connaît un certain nombre de termes , d’en déduire
les termes suivants ( loi de récurrence)
Ex : pour la suite 1 , qui est la suite
des nombres entiers naturels :
1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; …… ;
n ;…
On obtient chaque terme en ajoutant une unité
au terme précédent :
La loi de formation est :
u n = u n-1 + 1
Nous étudierons les deux types de suites, fondamentaux, la suite arithmétique dont la formation est
basée sur la loi simple de l’addition et la suite géométrique dont la formation est sur la loi
simple de la multiplication.
Ces études vont mettre en évidence des
analogies entre les progressions arithmétiques et les progressions
géométriques : elles sont formées de la même manière. (
par addition pour les progressions géométriques , par multiplication
pour les progressions géométriques) , leurs propriétés sont voisines. D’où l’idée du mathématicien Neper de comparer ces
progression et d’établir une correspondance entre les termes de même rang , et d’imaginer
« les logarithmes ».
Nomenclature
"suite" :
|
|
Ensemble |
"Suite" |
|
Désignation |
Par une lettre majuscule (R, N, D .) |
Par la lettre majuscule " U" |
|
Nom des éléments |
"nombres" |
Chaque élément pour le nom de "terme" |
|
Lettre utilisée pour désigner un élément |
|
Chaque terme est désigné par la lettre
minuscule "u" |
|
Les éléments sont ordonnés |
|
Chaque
terme est désigné par la lettre "u" indicé |
|
indice |
|
La valeur numérique de l'indice désigne le
"rang" du terme |
|
|
|
|
|
|
|
|
|
|
Les nombres pairs : 2 ;4 ;6 ;8 ;10 ;12 ;
(tous les nombres multiples de deux) |
|
|
Les nombres impairs1 ;
3 ; 5 ;7 ; 9 ; 11 ; …(
1+2n) .. « n désigne un nombre entier
naturel » |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
INTER DISCIPLINARITE: Trouver des cas ou l ' on peut parler d
' « ensemble »
TRAVAUX AUTO FORMATIFS :
(préparation du devoir)
|
CONTROLE: |
|
1 )
Qu'est ce qu'un ensemble ?
2 )
Par quoi nomme - t - on un ensemble (de nombres) ?
3 )
Comment nomme - t - on les objets d'un ensemble?
4 )Qu'est
ce qu'un ensemble "fini"?
5 )
Qu'est ce qu'un ensemble "infini"?
6 )
Comment écrit-on ,en écriture mathématique, "ensemble fini"?
7) Comment écrit-on , en
écriture mathématique , "ensemble infini" ?
8 )
Entre les deux écritures précédentes ,comment les différencie - t on ?
9) Donnez des exemples d'ensembles de nombres les
plus utilisés (4 au minimum)
10 ) Donnez le nom des ensembles de nombres
désignés par les lettres majuscules suivantes: N ; Z +ou- ;
D ;
D +ou- ; Q
; R
|
|
1) entourez les nombres
a ;b ; 7 ;c ;d ;
1 ; 11 ; l 2 ; 3 ; m ; o ; p ; 5 ;
g ; 6 ; 9 ; y ; u ; t ; 0 ; e ;
2 ; q ;s ; 4 ; r ; 8
2 ) Ranger les nombres suivants dans leur
ensemble :
(+63) ;
4 ; (-564) ; (+5,89 ) ; 267 ; (-
0,23) ; (+89,56) ; (+5) ; (- 781 ) ; (+125 ) ; 5 ;(+ 5678 ) ;
- (-5) ; 3 ;
(-89) ;(-1536) ; (+0.23) ;
(-5,89 ) ; 2567 ; (-89,56) ;
3 )
Construire un ensemble "E " fini
de 4 nombres relatifs,(les classer par ordre croissant)
4 )
Construire l'ensemble "S"
infini des nombres paires.
ALGEBRE:
|
Quel nom donne t on à "x";
"y";…. ,que représente - elle ? |
|
Donner un
exemple de valeur à "x"
et "y" pour chaque ensemble de
nombre
|
|
Soit "x" |
Soit "y" |
|
N |
|
|
|
D |
|
|
|
Z |
|
|
|
D+ ou- |
|
|
|
R |
|
|
|
Soit les deux écritures |
Qu'indique la valeur numérique? |
|
X2 |
|
|
X2 |
|