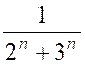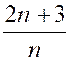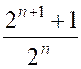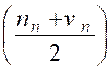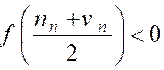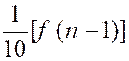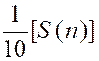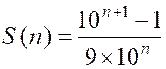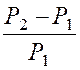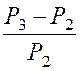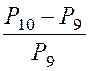|
|
|
Pré requis:
|
Définitions : les chiffres et
nombres |
|
Objectif suivant : |
DOSSIER: LES « SUITES » de NOMBRES
(présentation ;
généralités)
|
|
Exemples
de suites.. |
|
|
|
Notation |
|
|
|
Définition. |
|
|
|
Des
suites : ….
Arithmétiques ; géométriques ; encadrantes….. |
|
|
|
Exercices Types. |
|
|
|
|||||||
|
|
|
Devoir n°1
(première approche) |
|
|
|
|
|
|
COURS |
|
|
Exemples de « suites de
nombres » : |
|
|
|
|
|
|
|
On utilise fréquemment des suites de nombres
rangés dans un ordre déterminé. Exemples : La suite des nombres entiers naturels : 1 ; 2 ; 3 ; 4 ;
5 ; 6 ; 7 ; …… ; n ;… La suite des ouverture de
diaphragme d’un appareil
photographique : 2 ;
2 ,8 ; 4 ; 5,6 ; 8 ; 11 ; 16 ;
22 Les
suites des avances longitudinales et transversales ,
en mètres par minute , sur une fraiseuse : ·
: 9 ; 11 ; 14 ; 18 ;
23 ; 29 ; 36 ; 45 ; 58 ·
: 69 ; 86 ; 110 ; 137 ;
173 ; 220 275 ; 346 ;
440 « terme »
Chacun des nombres figurant dans une suite est un « terme » de
cette suite. « suite
finie ; suite infinie » Certaines suites comportent un nombre
fini de termes ( comme la suite 2 qui comprend 8
termes) . Ce sont des suites finies. D’autres comportent une infinité de termes , ce sont des suites infinies ou illimités ( par exemple : la suite 1) Notation : On représente en général les termes d’une suite
par une même lettre , chaque terme étant repéré par
un indice correspondant au rang qu’il occupe dans la suite. Ainsi pour
la suite 2 :
u1 = 2 ;
u2 = 2,8 ; u3
= 22 Il existe des suites dont les termes successifs
apparaissent au hasard. Mais , le plus souvent , on
définit une suite à l’aide d’une loi
de formation permettant : - soit de
calculer chaque terme en fonction de son rang : un = f ( n) Ex :Suite des
nombres entiers : u n
= n
Suite des nombres pairs :
un = 2 n -
Soit , lorsqu’on connaît un certain nombre de termes , d’en déduire les
termes suivants ( loi de récurrence)
|
|
|
|
Exemple : pour la suite 1 , qui est la suite des nombres entiers
naturels : 1 ; 2 ;
3 ; 4 ; 5 ; 6 ; 7 ; …… ; n ;… On obtient chaque terme en ajoutant une unité au
terme précédent : La loi de
formation est : u n = u n-1 + 1 Nous étudierons
les deux types de suites, fondamentaux, la suite arithmétique dont la formation est
basée sur la loi simple de l’addition et la suite géométrique dont la formation est sur la
loi simple de la multiplication. Ces études vont mettre en évidence des analogies
entre les progressions arithmétiques et les progressions géométriques :
elles sont formées de la même manière. ( par
addition pour les progressions géométriques , par multiplication pour les
progressions géométriques) , leurs propriétés sont voisines. D’où l’idée du mathématicien Neper de comparer
ces progression et d’établir une correspondance entre les termes de même rang , et d’imaginer
« les logarithmes ». |
|
|
|
Définition : |
|
|
|
Une suite est un ensemble d'éléments connus "en
compréhension". Une
"suite" est un
ensemble d ' éléments (de nombres) dont les éléments ont une propriété
caractéristique permettant de les reconnaître (identifier) ; Pour savoir si un élément "x"
appartient à une suite ,il faut se demander si l 'objet "x" possède ou non cette
propriété ; il est alors connu en compréhension. L'ordre des éléments est important ( croissant ou décroissant) ; ils
sont ou peuvent être "indicés" ( l'indice indique le numéro d'ordre ou de
rangement de ces éléments) |
|
|
|
Une suite de nombres réels est une application de
l’ensemble des entiers dans : R |
|
|
|
|
|
|
|
C’est donc une fonction numérique dont l’ensemble
de définition est N ( ou parfois N *
= N -
|
|
|
|
Si l’image d’un entier « n » est noté
« u n » , la suite elle-même
est notée : ( u n )
|
|
|
|
Une suite est dite « croissante »
(resp. décroissante) lorsque pour tout entier « n » on a
l’inégalité u n |
|
|
|
|
|
|
|
Les exercices 1 ; 2 ; 3 qui sont
proposés en fin de ce cours ; montrent des suites convergeant vers
« 0 » ; si petit que soit le nombre strictement positif
« On note u n |
|
|
|
Et l’on dit que ( u
n ) converge vers le réel « a » lorsque la suite
( u n – a ) converge « 0 » |
|
|
|
Deux types de suites se rencontrent souvent dans les
applications |
|
|
|
1°) Les
suites arithmétiques ( dites aussi « progressions arithmétiques ». |
|
|
|
Chaque terme est égal au précédent augmenté d’une constante
« b » ( appelée raison de la progression )
Le terme général s’écrit
alors : u n = u 0 +
nb |
|
|
|
2°) Les suites géométriques ( dites aussi « progressions géométriques) |
|
|
|
|
Chaque terme est égal au précédent multiplié par
une constante « q » ( appelée :
raison de la progression) |
|
|
|
|
Ce terme général s’écrit alors : u n = u 0 q n |
|
|
|
|
On peut vérifier que si la raison « q »
est telle que |
|
|
|
|
|
|
|
|
|
3°) Les Suites encadrantes. |
|
|
|
|
Deux suites
( u n ) et ( v n ) sont
dites encadrantes lorsque les quatre propriétés suivantes sont
vérifiées : |
|
|
|
|
( u n ) est croissante. |
|
|
|
|
( v n ) est
décroissante |
|
|
|
|
Pour tout entier « n » ( u n ) La suite ( v n - u n )
converge vers « 0 » On montre alors que les deux suites convergent
vers un réel « a » et que pour tout « n » : ( u n ) ( u n ) est une valeur approchée par défaut de
« a » ; ( v n
) est une valeur approchée par excès
de « a » ; une incertitude est ( v n - u n ) |
|
|
|
|
|
|
|
|
|
(info + sur : Les progressions
arithmétique et géométriques.) |
|
|
|
|
|
|
|
|
Exercices types
( série 4) |
|
||
|
1. |
On considère la suite définie par : u n = 1°) Calculer ses huit premiers termes
. 2°) Comment choisir « n » pour
que : ·
( u n ) < 0,1 ·
( u n ) < 0,01 ·
( u n ) < |
|
|
|
2. |
On considère la suite définie par u n = 1 °) Calculer ses huit premiers termes . 2°) Comment choisir « n » pour
que : ·
( u n ) < 0,1 ·
( u n ) < 0,01 ·
( u n ) < |
|
|
|
3. |
On considère la suite définie par u n = 1 °) Calculer ses huit premiers termes . 2°) Comment choisir « n » pour
que : ·
( u n ) < 0,1 ·
( u n ) < 0,01 ·
( u n ) < |
|
|
|
4. |
On considère la suite définie par u n = 1 °) Calculer ses dix premiers termes
. 2°) Montrer que , pour
tout entier « n » , on a les deux inégalités : ·
2 < u n ·
u n+1 < u n 3°) Peut-on déterminer « n » en sorte que ·
( u n – 2 ) < 0,1 ? ·
( u n – 2 ) <
·
|
|
|
|
5. |
On considère la suite définie par u n = 1 °) Calculer ses dix premiers termes
. 2°) Montrer que , pour
tout entier « n » , on a les deux inégalités : ·
2 < u n ·
u n+1 < u n 3°) Peut-on déterminer « n » en sorte que ·
( u n – 2 ) < 0,1 ? ·
( u n – 2 ) <
|
|
|
|
6. |
On considère la fonction définie sur
l’intervalle [ 1 ;
3 ] par f ( x ) = x² - 2 a) vérifier que « f »
est croissante. b) On définit deux suites ( u n ) et ( v n ) en
posant : u 1 = 1 ) et ( v 1 = 3
) et Si u n+1 = u n et
v n+ 1 = si u n+1
= vérifier que , pour tout
entier « n » f ( u n ) <
0 et
f ( v n ) c) Calculer : « u2 » ; « v2 » ; »u3 » ;
« v3 » ; « u4 » ; »v4 » ;
« u5 » ; « v5 » d) Vérifier que ( u n ) est une
suite croissante , que ( v n ) est une suite décroissante et que pour tout « n » ; (
u n ) < ( v n ) e) Montrer que ( v n ) - ( u n ) est une
suite convergeant vers « 0 ». Calculer les dix premiers termes . f) Donner un encadrement de |
|
|
|
7. |
On considère la fonction définie sur
l’intervalle [ 1 ;
3 ] par f ( x ) = x² - 3 a) vérifier que « f »
est croissante. b) On définit deux suites ( u n ) et ( v n ) en
posant : u 1 = 1 ) et ( v 1 = 3
) et Si u n+1 = u n et
v n+ 1 = si u n+1
= vérifier que , pour tout
entier « n » f ( u n ) <
0 et
f ( v n ) c) Calculer : « u2 » ;
« v2 » ; »u3 » ; « v3 » ; « u4 » ; »v4 » ;
« u5 » ; « v5 » d )
Vérifier que ( u n ) est une
suite croissante , que ( v n ) est une suite décroissante et que pour tout « n » ; (
u n ) < ( v n ) e ) Montrer que ( v n ) - ( u n ) est une suite convergeant vers « 0 ». Calculer les dix
premiers termes . f ) Donner un encadrement de g) Si votre calculatrice comporte une touche |
|
|
|
8. |
On définit une suite par « f
( 0) = 1 » ; « f ( n ) = 1°) Calculer « f ( n) »en
fonction de l’entier naturel « n ». exemple :
·
le premier terme est
« f (0) = 1 ; ·
le second terme est « f ( 1 )
= ·
le troisième
terme est f (2) =
·
le quatrième
terme est f (3) =
·
le 8 ième terme est
f ( 7)
= voir ci-dessus : Montrer que cette suite est
décroissante. Quelle est la valeur de
« f ( 8) » 2°) Pour tout entier « n » , on pose : « S (n) = f ( 0) + f ( 1) +………..+ f ( n) » a)
Calculer « S (3) = f ( 0) + f ( 1) + f ( 2 )+ f ( 3) » b) Montrer que En déduire que l’on a : |
|
|
|
9. |
L’étude de la production électrique française en
milliards de kilowattheures pendant dix années consécutives numérotées de
« 1 » à « 10 » a montré que les rapports :
( P n désignant la
production de l’année numérotée « n » ) étaient pratiquement constants et que leur valeur
commune était k = 0,1. 1°) Sachant que la production de l’année n°1
est P1 = 40
, calculer les valeurs de P2
, P3 , P4 . 2°)
« n » désignant un entier compris entre « 1 » et
« 9 » , P n+1 la production de
la ( n+1)ième année, trouver une relation simple entre P n et P n+1. Calculer P n en fonction de P1 ;
en déduire la valeur de P 10. 3°) A partir de quelle année la production
a-t-elle été au moins le double de P 1 . ? |
|
|
|
10. |
A suivre !!!!! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Progressions : "Suite"
: de nombres :
Nomenclature
"suite" :
|
|
Ensemble |
"Suite" |
|
Désignation |
Par une lettre majuscule (R, N, D .) |
Par la lettre majuscule " U" |
|
Nom des éléments |
"nombres" |
Chaque élément pour le nom de "terme" |
|
Lettre utilisée pour désigner un élément |
|
Chaque terme est désigné par la lettre
minuscule "u" |
|
Les éléments sont ordonnés |
|
Chaque
terme est désigné par la lettre "u" indicé |
|
indice |
|
La valeur numérique de l'indice désigne le
"rang" du terme |
|
|
|
|
|
|
|
|
|
|
Les nombres pairs : 2 ;4 ;6 ;8 ;10 ;12 ;
(tous les nombres multiples de deux) |
|
|
Les nombres impairs1 ;
3 ; 5 ;7 ; 9 ; 11 ; …(
1+2n) .. « n désigne un nombre entier
naturel » |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
INTER DISCIPLINARITE: Trouver des cas ou l ' on peut parler d
' « ensemble »
TRAVAUX
AUTO FORMATIFS : (préparation du devoir)
|
CONTROLE: |
|
1 ) Qu'est ce qu'un ensemble ?
2 ) Par quoi nomme - t - on un ensemble (de nombres) ?
3 ) Comment nomme - t - on les objets d'un ensemble?
4 )Qu'est ce qu'un ensemble "fini"?
5 ) Qu'est ce qu'un ensemble "infini"?
6 ) Comment écrit-on ,en écriture mathématique, "ensemble fini"?
7) Comment écrit-on , en
écriture mathématique , "ensemble infini" ?
8 ) Entre les deux écritures précédentes ,comment les différencie - t
on ?
9) Donnez des exemples d'ensembles de nombres les
plus utilisés (4 au minimum)
10 ) Donnez le nom des ensembles de
nombres désignés par les lettres majuscules suivantes: N ; Z +ou- ;
D ;
D +ou- ; Q
; R
|
|
1) entourez les nombres
a ;b ; 7 ;c ;d ;
1 ; 11 ; l 2 ; 3 ; m ; o ; p ; 5 ;
g ; 6 ; 9 ; y ; u ; t ; 0 ; e ;
2 ; q ;s ; 4 ; r ; 8
2 ) Ranger les nombres suivants
dans leur ensemble :
(+63) ;
4 ; (-564) ; (+5,89 ) ; 267 ; (-
0,23) ; (+89,56) ; (+5) ; (- 781 ) ; (+125 ) ; 5 ;(+ 5678 ) ;
- (-5) ; 3 ;
(-89) ;(-1536) ; (+0.23) ;
(-5,89 ) ; 2567 ; (-89,56) ;
3 ) Construire un ensemble "E " fini de 4 nombres relatifs,(les classer par ordre
croissant)
4 ) Construire l'ensemble
"S" infini des nombres paires.
ALGEBRE:
|
Quel nom donne t on à "x";
"y";…. ,que représente - elle ? |
|
Donner un
exemple de valeur à "x"
et "y" pour chaque ensemble de
nombre
|
|
Soit "x" |
Soit "y" |
|
N |
|
|
|
D |
|
|
|
Z |
|
|
|
D+ ou- |
|
|
|
R |
|
|
|
Soit les deux
écritures |
Qu'indique la valeur
numérique? |
|
X2 |
|
|
X2 |
|