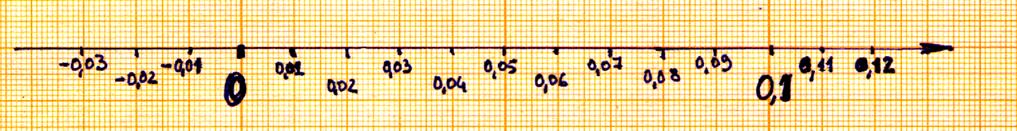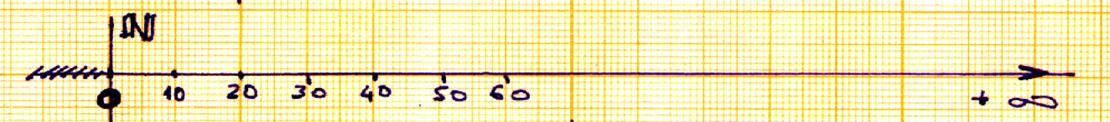Pré requis
|
Les ensembles de nombres |
|
|
Relations d’ordre dans les nombres entiers naturels |
|
|
Nomenclature (terminologie) |
ENVIRONNEMENT du dossier
|
Objectif précédent : >>> voir papier millimétré. |
Objectif suivant : |
Tableau |
|
DOSSIER REPRESENTATION
GRAPHIQUE des NOMBRES ,sur papier millimétré :
1. Le papier millimétré ; précision (0,1 ;0,01 ; 0,001 )
2. Représentation des N
3. Représentation des Décimaux positifs
4. Représentation des décimaux relatifs
5. Représentation des réels.
|
TEST |
COURS |
Interdisciplinarité |
|
COURS
Pour la REPRESENTATION
GRAPHIQUE DES NOMBRES nous utilisons du papier millimétré :
(nous pouvons
aussi construire un axe gradué ![]() sur une feuille quadrillée )
sur une feuille quadrillée )
Un papier est vendu
pour effectuer des représentations graphiques : on le nomme le papier millimétré ! ! ! ! !
Cas courant : c’est une feuille au format A4 (
Cette feuille est « quadrillée » :
Elle est divisée en carreaux de
Précision à 1 + ou – 0,1:
|
« dixième
d’unité ». Chaque graduation « 1 unité » peut se
subdiviser en 10 parties égales.(nous
obtenons les dixièmes d’unités) exemple : nous pouvons placer un point en « +
1,1 » |
|
|
Précision à 0,1 + ou –
0,1:
|
l’unité est divisée en 10 parties égales ( 0,1
par 0,1) ; ces divisions sont divisées en 10 parties égales ( soit chaque
graduation représente 0,01 unité) exemple : nous pouvons placer un point en « +
1,12 » |
|
|
Précision à 0,01 + ou –
0,1:
|
Nous pourrions obtenir des « millièmes d’unités » chaque
subdivision précédente peut encore se
diviser en 10 parties égales. (nous
obtenons les millièmes d’unités) :
exemple : nous pouvons
placer un point en « + 1,112 » |
|
|
Représentation
graphique des nombres :
|
Représentation graphique des nombres entiers naturels : Précision à 1 + ou - 0,1 |
|
|
|
|
|
Représentation graphique des nombres entiers
naturels : Précision : 1+ ou -1 |
|
|
|
|
|
Représentation
graphique des nombres
entiers relatifs : Précision : 1+ ou -1 |
|
|
|
|
LES DECIMAUX Lpositifs et relatifs .
|
Représentation graphique des nombres décimaux
positifs : Précision : 0,1 / 10
= 0,01 |
|
|
|
|
|
Représentation graphique des nombres décimaux
positifs : Précision : 0,1/20 = 0,005 |
|
|
|
|
|
Représentation graphique des nombres décimaux positifs : Précision : 1 / 10 = 0,1 |
|
|
|
|
Représentation graphique des
nombres décimaux relatifs :
|
|
|
Les nombres relatifs
« opposés » sont dit « symétriques ».
Exemple : 5 et –5 sont symétriques par rapport à 0
LES REELS
|
On peut placer « approximativement » des nombres
réels : |
|
|
|
|
![]()
 » 1,414 ;
» 1,414 ;
 p = 3,14
p = 3,14
TRAVAUX AUTO - FORMATIFS
Que veut dire
« graduer »?
Quelle est la fonction du segment
unitaire?
EVALUATION
A )
GRADUATION avec règle graduée:
Série 1 :Conditions :
l’unité 1 à pour mesure
1°) Graduer une droite avec des entiers
naturels .( N ) inférieur à 10
2°) graduer une droite avec des nombres décimaux positifs
( allant de 0,5 en 0,5 ) inférieur à 10
3°) graduer une droite avec des nombres décimaux positifs
( allant de 0,25 en 0,25 ) inférieur à 10
4°)Graduer une droite avec des nombres entiers
relatifs compris entre –10 et +10
5°) graduer une droite avec des nombres décimaux relatifs
( allant de 0,5 en 0,5 ) inférieur à 10
6°) graduer une droite avec des nombres décimaux relatifs
( allant de 0,25 en 0,25 ) inférieur à 10.
Série 2 : Conditions :
l’unité 1 mesure
1°)
Graduer une droite avec des entiers naturels .(
N ) inférieur à 10 , supérieur à -5
2°) graduer une droite avec des nombres
décimaux positifs ( allant de 0,5 en
0,5 ) inférieur à 10 supérieur à -5
3°)
graduer une droite avec des nombres décimaux
positifs (
allant de 0,25 en 0,25 ) inférieur à 10 supérieur à -5
4°)Graduer une
droite avec des nombres entiers relatifs compris entre –10 et +10 supérieur à
-5
5°) graduer une droite avec des nombres
décimaux relatifs ( allant de 0,5 en
0,5 ) inférieur à 10 supérieur à -5
6°) graduer une droite avec des nombres
décimaux relatifs ( allant de 0,2 en
0,2 inférieur à 10 supérieur à -5.
7 ° )
Exercices : Sur une droite graduée
placer les points suivants :
p ; 1/3 ; -1,2 ; ![]()
![]() ;
;![]() ;
;![]()
.