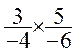Pré requis:
|
|
|
|
|
ENVIRONNEMENT du dossier:
|
Objectif précédent : |
Objectif suivant : |
Liste
des cours en calcul numérique |
|
|
|
|
|
|
DOSSIER : NOTIONS sur : LES
NOMBRES « POSITIFS » ET
« NEGATIFS »
Ces nombres sont aussi appelés : « nombres algébriques. »
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TEST |
COURS |
Devoir Contrôle |
Devoir évaluation |
|
|
Corrigé Contrôle |
Corrigé évaluation |
|
|
|
|
|
|
|
|
COURS
Origine et signification des nombres
« positifs » et « négatifs » :
Il arrive fréquemment
que l’on considère des grandeurs susceptibles d’être comptées dans deux sens
opposés : par exemple :
Le temps peut être compté dans le présent
ou dans l’avenir
Une longueur sur une droite peut être portée
dans un sens ou dans l’autre à partir de l’un de ses points ;
Les sommes qu’inscrit un commerçant sur son
livre de caisse peuvent être des « recettes » ou des
« dépenses » ; etc.
Dans ces divers cas ,
il est commode , au lieu d’employer un langage plus ou moins long pour indiquer
quel est le sens de la grandeur qui correspond à un nombre donné , de convenir
d’une « notation abrégée » ; telle est l’origine des nombres
négatifs et positifs.
Exemples :
|
Au lieu
d’inscrire « 50 € de recettes » , nous
pourrons écrire |
+ 50 € |
|
Au lieu
d’inscrire « 35 € de dépenses » , nous
pouvons écrire |
- 35 € |
|
Au lieu
d’écrire que le thermomètre marque 3° au dessus de zéro , nous dirons
qu’il marque |
+ 3° |
|
Au lieu
d’écrire que le thermomètre marque 7 °
au dessous de zéro , nous
dirons qu’il marque |
- 7° |
|
Et ainsi de suite …….. |
|
Mais cet
avantage est loin d’ être le seul que présente
l’introduction de ces nombres ; de plus , ce que nous venons de dire ne
suffit pas à faire comprendre pourquoi
on emploie , pour les distinguer , les signes
+ et - de l’addition et de la soustraction, plutôt
que d’autres signes quelconques.
Nous le comprendrons mieux en résolvant le problème
suivant :
Problème : Un habitant de Lyon voyage fréquemment sur
la ligne Paris- Lyon – Marseille. Chaque
jour il note la distance à laquelle il se trouve de Lyon .
Il marque aujourd’hui
Commentaire :
On ne peut pas
répondre à cette question , car les
données sont insuffisantes.
Le voyageur
peut être à
Pour désigner
ces deux sens , on convient de désigner l’un d’eux sous le nom de « sens
positif » , soit par exemple de
Lyon vers Marseille , l’autre inverse , sous le nom de « sens
négatif ».
Si le voyageur
s’est éloigné de Lyon de
+ 70 et – 70 sont des nombres , l’un « positif »
et l’autre « négatif » .Cette notation est très avantageuse comme « langage abrégé ».
Il est , en
effet, plus court de dire ou d’écrire :le voyageur est à +
Les autres avantages de cette écriture :
Calculons la
distance qui sépare notre voyageur de Paris .
Si le voyageur
est à +
on pourrait écrire :
Si ,au
contraire, sa distance de Lyon est
de –
on
pourrait écrire :
On voit que , dans les deux cas , la distance du
voyageur à Paris s’obtient en écrivant à la suite de la distance de Paris à
Lyon
Second exemple :
Un
commerçant avait en caisse au début de la journée 1500 € . Il vient de recevoir 270 € , puis il a payé une première
note de 50 € et une deuxième note
de 120 €. Quel est son avoir en
caisse ?
Nous
convenons d’appeler « positives » les sommes versées en caisse et
« négatives » les sommes déboursées .Les trois opérations indiquées
s’inscriront :
+ 270 € – 50 € – 120 €
ou encore la somme des trois opérations se noterons : (+ 270 € ) + ( –
50 € ) + ( – 120 € )
On
voit aisément que l’avoir en caisse s’obtient en calculant comme suit :
1200 + 270 = 1470
1470 – 50
= 1420
1420 – 120 = 1 300
l’avoir
en caisse est de 1 300 €.
Il a
suffi d’écrire les nombres à la suite dans l’ordre où ils se présentent et
d’effectuer successivement les opérations indiquées par leurs signes .
Règles de
calcul sur les nombres positifs et négatifs
Nous allons
reprendre d’une manière plus précise la définition des nombres positifs ou
négatifs et montrer en même temps comment on peut en déduire les règles des
opérations à effectuer sur ces nombres .(dans l’ordre on abordera :
l’addition et la soustraction , ensuite
la multiplication et la division.
Nous utiliserons les « segments »de
droites pour apporter d’autres précisions :
Nous considérons d’abord le cas où les nombres
positifs et négatifs servent à mesurer des longueurs comptées dans des sens
opposés.
Pour avoir une image aussi simple
que possible, nous utiliserons comme figure géométrique une droite indéfinie sur laquelle nous aurons choisi un
sens de parcours que nous appellerons « sens positif » et que nous
indiquerons par une flèche ; une telle droite s’appelle un « axe
orienté » ou , plus
brièvement , un axe . Le sens opposé au
sens positif est le « sens négatif ».
On peut se figurer un promeneur qui marcherait sur l’axe , allant
tantôt en avant , tantôt à reculons , mais en regardant toujours « vers la direction
positive » .
B
A
Pour aller
de A vers B , le voyageur marcherait en avant , et pour aller de B vers A , il irait à reculons.
Si ce
promeneur fait des pas égaux , il peut mesurer les distances en comptant le
nombre de ses pas .
Nous
considérerons comme « positifs » les pas faits en avant , et comme
« négatifs » les pas faits à reculons ; de telle sorte que s’il
lui faut 40 pas pour parcourir la distance AB , on dira que de A vers B il y a
+ 40 pas et que de B vers A il y a – 40 pas .
On
donne le nom de « segment » à une portion d’un axe lorsqu’on porte
son attention sur le sens dans lequel elle parcourue.
Ainsi
lorsque le voyageur va de A vers B , nous dirons qu’il
parcourt le segment AB ( on notera le parcours de A vers B : 
) (info plus : algèbre) ; lorsqu’il va de B vers A , nous
dirons qu’il parcourt le segment BA ( on
notera le parcours de B vers A : 
)
Ainsi n’est pas la même
chose que . (on les
appelle en algèbre : « mesure algébrique » )
Ce n’est pas
la même chose d’aller de Paris à Lyon ou de Lyon à Paris. Dans les deux cas on
parcourt la même distance désignée indifféremment par la notation AB ou BA ,
mais on ne marche pas dans le même sens.
Equivalents algébriques des
segments.
Pour exprimer
que notre promeneur fait + 40 pas pour parcourir le segment
, nous
écrirons : = + 40 ,
ou = 40
on écrirait au contraire : = - 40
puisqu’il faut faire – 40 pas pour parcourir le segment , c’est à dire
faire 40 pas à reculons pour aller de B vers A.
Les nombres 40
et –40 s’appellent les
« équivalents algébriques » des segments et , l’unité choisie étant le pas du promeneur.
Commentaire : bien entendu , on pourrait choisir toute
autre unité ; la seule chose essentielle , c’est de bien préciser quelle
unité on choisit et de ne pas en changer dans le cours d’une même question .
L’
équivalent algébrique d’un segment ne dépend pas seulement de l’unité de longueur
choisie, il dépend aussi du sens choisi comme positif sur l’axe .
Si la figure restant par ailleurs la même , on
changerait la direction de la flèche , c’est qui aurait pour
équivalent – 40 et qui aurait + 40 .
Il en est de
la direction positive comme de l’unité de longueur , on peut la choisir
arbitrairement au début d’une question , mais il est essentiel qu’elle soit
bien précisée et qu’elle ne change pas dans le courant de la question .
La longueur 40 est
dite la « valeur absolue » des nombres + 40 et – 40 ;c’est la
longueur commune des segments AB et BA ; ou , si l’on veut , la distance
géométrique de AB ou BA .
D’une manière générale , on
appelle valeur absolue d’un nombre positif ou négatif le nombre que l’on
obtient en supprimant le signe .
La valeur absolue d’un nombre positif est égale à ce nombre.
Deux
segments situés sur un même axe sont dits égaux lorsqu’ils ont même équivalent
algébrique ; il doivent avoir même
longueur et même sens .
A D
B
C
Les segments AB et CD sont
égaux . Mais le segment AB n’est pas égal au segment DC , ce segment DC est
égal au segment BA.
Les segments AB et BA sont dit opposés , on dira aussi que
les segments DC et AB sont opposés , puisque le segment DC est égal à BA .
Les équivalents
algébriques de deux segments opposés sont deux nombres tels que + 40
et – 40 égaux en valeur absolue
et de signes contraires (on dit parfois plus brièvement mais incorrectement ,
égaux et de signes contraires ), nous dirons aussi que ces nombres sont
opposés.
|
SOMME de deux nombres . |
Supposons que notre promeneur fasse
7 pas en avant , et ensuite 3 pas en reculons ; il parcourt d’abord
, un segment de = +7 , et ensuite un
segment 
= - 3
Il est clair qu’il
serait arrivé au même point C en faisant simplement 5 pas en avant
, c’est à dire en parcourant le segment de 
= + 4
Ainsi parcourir successivement
les segments de mesure et revient à parcourir le
segment . Nous exprimerons ce
fait en disant que le segment est la somme des
mesures algébriques des segments et et
nous écrirons
= +
On voit là quelle différence sépare la notion de segment (mesure
algébrique) de la notion de longueur ; la longueur AB est de 7 pas , la longueur BC de 3 pas : leur
somme est donc est 10 pas.
Et ,de fait, le promeneur qui parcourt successivement ces deux longueurs
fait bien 10 pas en tout et non pas 4 . Seulement , comme il en fait 3 à
reculons , le point où il arrive est le
même que s’il avait fait seulement 4 pas
en avant.
Lorsque l’on considère les segments au lieu des longueurs , on ne se
préoccupe que de ce point final , on ne s’inquiète pas de la fatigue du promeneur qui aurait pu
faire 503 pas en avant et 500 à
reculons ; on désire seulement
savoir en quel point il arrive.
La mesure algébrique du segment
AC , à savoir + 4 est dite la « somme » des valeurs algébriques des
segments AB et BC , c’est à dire de 7 et de – 3 ; nous pouvons
écrire : 7 +( - 3 ) = 4
On vérifierait :
Que : 7 + 3
= 10
( ainsi : 7 pas en avant plus 3 pas en avant
équivalent à 10 pas en avant )
De même que :
-7 + 3 = - 4
( ainsi : 7 pas en
arrière et 3 pas en avant équivalent à 4
pas en arrière )
de même enfin :
que - 7 –3
= - 10
( ainsi : 7 pas en arrière et 3 pas en reculons équivalent à 10 pas en reculons )
Nous venons de voir un cas particulier , de ce cas nous pouvons obtenir la règle d’addition
de deux nombres .
|
Règle d’addition : |
Pour obtenir la somme de deux nombres de même signe , on ajoute leurs valeurs absolues et l’on
affecte la somme du signe commun.
Pour obtenir la somme de deux nombres de signes contraires , on
retranche la plus petite valeur absolue de la plus grande et on affecte à la
différence le signe de la plus grande .
Exemples :
3 + (-4) = -1
125 + ( - 210 ) = - 85
-3250 + ( - 3 ) = - 3253
- 100 + 2 = - 98
- 1010 + ( 2000 ) = 900
134 + ( - 134 ) = 0
remarque :
On voit que la somme de
deux nombres opposés est toujours égale à zéro ; faire un certain nombre
de pas en avant , et ensuite le même nombre de pas à reculons , équivaut à ne
pas bouger , à ne faire aucun pas .
Somme de plusieurs nombres .
Ce calcul nous l’avons déjà fait dans l’exemple
suivant :
Un commerçant avait en caisse au début
de la journée 1500 € . Il vient de recevoir
270 € , puis il a payé une première note de 50 € et une deuxième note de
120 €. Quel est son avoir en
caisse ?
Nous convenons d’appeler
« positives » les sommes versées en caisse et « négatives »
les sommes déboursées .Les trois opérations indiquées s’inscriront :
+ 270 €
– 50 € – 120 € ou encore la somme des trois opérations se
noterons : (+ 270 € ) + ( – 50 € ) + ( – 120 € )
On voit aisément que l’avoir en caisse
s’obtient en calculant comme suit :
1200 + 270 = 1470
1470 – 50
= 1420
1420 – 120 = 1 300
l’avoir en caisse est de 1 300 €.
Il a suffi d’écrire les nombres à la
suite dans l’ordre où ils se présentent et d’effectuer successivement les
opérations indiquées par leurs signes .
C’est
le résultat que l’on obtient en ajoutant
le second au premier , le troisième à la somme ainsi obtenue , la
quatrième à cette nouvelle somme , etc.
L’opération
se réduit donc à une série d’additions de deux nombres qu’on effectue en
appliquant la règle ci
dessus indiquée.
Ainsi
la somme :
12 + (
- 5 ) + ( - 28 ) + 13
s’obtiendra
comme suit :
12 +
(-5 ) = 7
7 + (
- 28 ) = -21
-21 +
13 = - 8
la
somme demandée est –8
Théorèmes relatifs à la somme de
plusieurs nombres
On peut établir quelques propositions qui
permettent d’obtenir autrement le même résultat et le plus souvent d’introduire
ainsi dans les calculs des simplifications commodes.
Théorème 1 :
La somme de plusieurs nombres ne change pas quand on intervertit leur
ordre .
Par exemple , l’on a
13 + ( -5 )+ ( -28) +17 = -5 + 13 + 17 + (-28)
en effet , supposons que Paul ait
à recevoir 13 € de Pierre et 17 € de
Francis et qu’il doit payer une note de
5 € chez le boulanger et 28 € chez le boucher . Il est évident que sa
situation finale est la même quel que soit l’ordre dans lequel il règle ces
opérations , qu’il recouvre d’abord une
créance et pour cela qu’il commence par
Francis ou par Pierre ; qu’au contraire il paye ses dettes et pour
cela qu’il aille d’abord chez le boucher ou chez le boulanger. Cette situation
reste toujours qu’il a –3 € de dette ,
qu’il possède – 3 €.
On trouverait aisément une
démonstration analogue pour les théorèmes suivants qui sont d’un usage
commode :
Théorème 2 :
On ne change pas la valeur d’une
somme en remplaçant plusieurs de ses
parties par leur somme effectuée.
13 + ( -5 )+ ( -28) +17 = -5 + 13 + (-11)
Théorème 3 : pour calculer la somme de plusieurs nombre
, on peut procéder comme suit : additionner les valeurs absolues des
nombres positifs ; additionner les valeurs absolues des nombres négatifs ;
retrancher la plus petite de ces sommes de la plus grande , et donner le signe
de la plus grande .
13 + ( -5 )+ ( -28) +17 = 30 + (-
33)
commentaire : suivant le cas , il peut être
commode d’utiliser le premier ou le
deuxième de ces théorèmes.
« 357 + ( - 324 ) + 325 + (-34) + 4 »
on remarque que l’on à
( - 324 ) + 325 = 1
(-34) + 4 = -30
de sorte que l’on aura à calculer : 357 +1 – 30 = 328
SOUSTRACTION
|
Définition . La soustraction est l’opération inverse de
l’addition.
Retrancher un nombre d’un autre ,
c’est en trouver un troisième qui ,ajouter au premier, reproduise le second .
Exemple :
Si l’on retranche 3 de 5 , on trouve 2
, car 2 + 3 = 5
Si l’on retranche –3 de 5 , on
trouve 8 , car 8 +(-3) = 5
Si l’on retranche 5 de –3 , on trouve –8 , car –8 + 5 = 3
Règle de la soustraction .
Pour retrancher un nombre quelconque , il suffit d’ajouter le nombre
opposé .
Ainsi ,pour retrancher « 3 » , il suffit d’ajouter –3 ;
pour retrancher –3 , il suffit d’ajouter
« 3 ».
Ce principe peut être regardé
comme une conséquence des exemples donnés ; on peut le démontrer
rigoureusement en remarquant que la somme de deux nombres opposés et nulle , on
a :
7 + 3 + (-3 ) = 7
7 + (-3) +
3 = 7
dans la première égalité 7 + 3
est le nombre qu’il faut ajouter à ( - 3 ) pour avoir 7 ; dans la deuxième égalité
, d’après la définition même de la soustraction 7 + ( -3 ) est la différence de
7 et de 3.
La démonstration serait la même si au lieu de 7 on avait un nombre
négatif tel que -8 .
La soustraction se ramène donc à l’addition ; soit par exemple à
effectuer le calcul de l’expression
4 - ( - 5 ) + ( -7 ) – ( + 4 ) - ( - 3 ) + 12
on pourra écrire : 4 + ( + 5 ) + ( -7 ) + ( - 4 )
+ ( + 3 ) + 12
de manière qu’il n’y ait
plus que des additions à effectuer ; et l’on appliquera les règles que
nous avons données dans l’addition.
Les théorèmes démontrés pour le cas
d’additions successives s’appliquent aussi dans le cas de soustractions ;
en particulier , on ne change pas le résultat final en intervertissant l’ordre
des opérations ; on a par exemple :
4 – ( -3 ) + ( -5 ) – (-7) = 4 – ( - 7) – ( - 3 ) + ( -5 )
REMARQUE : (approche
« algèbre »)
Lorsqu’on désigne les nombres par des lettres , il peut arriver qu’une
lettre représente un nombre négatif tel que ( - 5 ) ; alors le symbole
« - a » signifie que l’on doit retrancher « -5 » , c’est à
dire que l’on doit ajouter 3 ; donc :
- ( -3 ) = + 3
D’ une manière générale ,
« -a » désigne le nombre opposé au nombre « a »
On se trouve amené ainsi parfois à superposer en quelque sorte plusieurs
signes - ; il en résulte des
explications précédentes que deux signes
« - » peuvent être
supprimés ou , ce qui revient au même , remplacés par le signe « + »
Ainsi lorsque « a » désigne – 3
-a = - ( -3 ) = + 3
Si l’on a à retrancher –a , cela revient à ajouter « a » ,
c’est à dire à retrancher 3 .
-
[- (-3 ) ] = - 3
Dans ce cas , nous avions trois signes
« - » ; si l’on en suppriment deux , il n’en reste plus
qu’un .
· Applications :
1°) soit à calculer l’expression :
a – b – ( - c ) + ( - d )
où l’on suppose : a =
10 , b =
- 4 , c = 3 , d = -7
on obtient
10 – ( - 4
) – ( - 3 ) + ( - ( -7 ) ) =
10 + 4 + 3 + 7 = 24
2°) calculer l’
expression : - a – (– b) + ( - c )
- ( - d )
où l’on suppose :
a = 4 ,
b = - 6 , c = - 3
, d = 7
on obtient - 4 – 6 + 3 + 7 = 0
on peut trouver d’autres
exemples aux exercices précédents .
Théorèmes
relatifs à la soustraction .
Théorème 1 :
Pour retrancher une somme d’un nombre , il suffit d’en retrancher
successivement les divers parties de la somme.
Par exemple :
7 -[ 5 + (-3) + (-7 ) +2 ] = 4 –
5 – ( -3 ) – (-7 ) –2
= 4 – 5 + 3 + 7 – 2
ce théorème résulte directement de la définition même de la
soustraction car , en ajoutant au second
membre la somme qui figure entre crochets au premier membre , on obtient bien
« 4 » ; il suffit , pour faire cette addition , d’appliquer les
théorèmes relatifs à la somme de plusieurs nombres , les
termes +5 , - 5 ; - 3 ; +3 ,
etc. se « détruisent » ou
« neutralisent » deux à deux .
théorème 2 :
Pour retrancher d’un nombre la différence de deux autres , il suffit
d’en retrancher le premier et d’ajouter le second au résultat obtenu.
Ainsi : - 7 – [6 – ( -3 )]
= -5 –6 + ( -3 )
Car le nombre opposé à 6 – ( -3 ) ou 6 + 3
est - 6 + (-3 )
REMARQUE importante :
Règle pratique
On conclut des théorèmes précédents que toute parenthèse précédée du signe +
peut être supprimée , tandis que
, si l’on supprime une parenthèse
précédée du signe - , il faut changer
les signes qui précédent les nombres placés à son intérieur.
Dans l’application de cette règle pratique , on doit avoir grand soin
d’observer que , dans le cas où plusieurs signes se trouvent superposés devant un même nombre
, il ne faut changer que l’un d’eux .
Soit , par exemple , à calculer
l’expression suivante :
5 – [2 – ( - 3 )
] on obtiendra : 5 – 2 + ( - 3 )
On a eu soin de changer l’un des signes – qui précédaient 3 , mais on
n’a pas changé les deux .
Pratiquement , d’ailleurs , on évitera le plus possible ces
superpositions de signes , en effectuant immédiatement les opérations indiquées
.
Par exemple : 5 – [2 – ( - 3
) ] deviendra de suite : 5 – [2 + 3
]
MULTIPLICATION
|
La notion concrète
d’addition algébrique nous a été donnée
par l’examen des segments de droite , nous avons pu en déduire aisément la règle
de calcul.
Nous allons procéder aussi par une étude concrète , celle du mouvement
uniforme pour bien faire comprendre ce
que signifie la multiplication des nombres positifs et négatifs et quelle est
l’origine de la règle d’opération.
Considérons un promeneur , figuré par le point A se déplaçant sur un axe
dans les conditions indiquées plus haut à propos des segments
.On dit que le mouvement du point A est « uniforme » lorsque les
espaces qu’il parcourt dans les temps égaux sont toujours égaux .
Ainsi l’espace parcouru pendant une heure est toujours le même ,
l’espace parcouru pendant une minute est toujours le même, etc.
Dans cette définition , il ne faut pas perdre de vue que le point A se
déplace sur un axe , c’est à dire que
les espaces ne sont considérés comme égaux que s’ils sont égaux en valeur absolue , et
de même signe .
Un promeneur qui marche d’un pas égal sur une route se déplace à peu
près d’un mouvement uniforme , s’il se dirige toujours dans le même sens , il
n’en est pas de même s’il se promène de long en large dans un corridor.
On appelle « vitesse » d’un mouvement uniforme l’espace
parcouru pendant l’unité de temps.
Pour déterminer la vitesse , il est donc nécessaire de connaître :
1°) le mouvement ; 2°) le sens choisi comme sens positif ;3°)
l’unité de longueur ; 4°) l’unité de temps .
Il résulte de la définition de
la vitesse que c’est un nombre positif ou négatif , suivant que le mobile se déplace dans le
sens positif ou le sens négatif .
Problème .
Proposons – nous de trouver quel est l’espace parcouru dans un temps
« t » , la vitesse étant « v ».
1er cas .
supposons par exemple que notre promeneur fasse 3 pas à la seconde , qu’il se dirige à partir de « A »
dans le sens positif , quel est l’espace
parcouru ( en pas ) au bout de 4 secondes ?
La vitesse s’exprime en
(+ 3) , et le temps par (+4) .
Le promeneur fait en 4 secondes 3
fois 4 = 12 pas ;
Ces 12 pas sont parcourus dans le sens positif , l’espace parcouru
= +12
Nous exprimerons cela comme il suit : (
+3 )
( +4) = ( + 12)
Nous dirons que : +12 est
appelé « produit algébrique » de +3 par + 4 .
2ième CAS.
Supposons que le promeneur
aille à reculons , sa vitesse
est de « –3 »
Il parcourt en 4 secondes
3 fois 4 = 12 pas
, comme précédemment ,
mais le segment qu’il parcourt
B A
est dirigé dans le sens négatif ,
il est donc exprimé par –12
–12 est le produit algébrique de
–3 par + 4
On exprimera ce résultat (-3 ) ( +4 ) = -12
3ième Cas :
Supposons que le promeneur marche en avant , proposons –nous de trouver
l’espace parcouru pendant le temps - 4
secondes .
Que faut-il entendre par « espace parcouru » pendant un temps
négatif ?
A « l’époque actuelle »
le mobile est en A , au temps moins 4 ; ( - 4 ) , c’est à dire
« il y a 4 secondes , il était en « B » , nous disons que le
segment est
Est l’espace qui correspond au temps -4
Comme l’espace parcouru pendant
le temps + 4 est le segment qu’il
faut parcourir pour , de la position
actuelle , aller à la position occupée à l’époque + 4 .
Pendant ces 4 secondes , le promeneur a fait encore 3 fois 4 = 12 pas , puisqu’il se déplace dans le sens positif , c’est qu’il était il y a 4 secondes
à gauche de A ; le segment est donc négatif. Nous
exprimons cette observation comme il
suit : ( +
3 ) ( -4) = - 12
Le
produit algébrique de +3 par – 4 est –12
4ième
Cas :
Supposons enfin que la vitesse et le temps soient
négatifs le voyageur se déplace à reculons
, il est actuellement en A . Où était-il il y a 4 secondes ?
L’examen direct de
la question nous montre qu’il était à droite de A à 12 pas ; le segment est donc positif .
Nous écrivons : (-3) ( -4)
= + 12
Le
produit algébrique de –3 par – 4 est + 12
L’étude de ces cas particuliers que nous avons tenu à détailler nous
permet d’énoncer la règle suivante de la
multiplication .
Règle de la multiplication .
Le produit de deux nombres positifs
ou négatifs est un nombre dont la valeur absolue est égale au produit des
valeurs absolues des facteurs .
Ce nombre est positif dans le cas où les deux facteurs sont de même
signe .Il est négatif si ces facteurs
sont de signes contraires .
Applications :
3 5 = 15
3( -
5 ) = - 15
- 3 5 = - 15
- 3 ( - 5) = + 15
Produit de
plusieurs facteurs.
Le produit de plusieurs facteurs est , par définition , le résultat
final que l’on obtient lorsqu’on
multiplie le premier facteur par le second , le produit obtenu par le troisième
, le produit obtenu par le quatrième , etc.
Ainsi , soit le produit :
-3 4(-5) 6(-2) 2
il s’effectue comme suit :
-34 = -12
-12 -5 = 60
60 6 = 360
360 -2 = -720
-720 2 = -1440
le produit considéré a pour valeur - 1440
Signe du produit de plusieurs facteurs .
D’après la règle précédente ,
lorsqu’on effectue le produit de plusieurs facteurs , on voit que chaque
facteur négatif entraîne un changement
de signe , tandis que chaque facteur positif n’en entraîne pas ;
On en conclut que le signe du produit ne dépend que du nombre de
facteurs négatifs ; si ce non est paire ou nul , le produit est
positif : si ce nombre est impair le produit est négatif.
Cette remarque permet d’obtenir rapidement le produit : on
détermine d’abord son signe , il suffit ensuite d’effectuer le produit des
valeurs absolues des facteurs.
Propriétés du produit de plusieurs facteurs .
Théorème :La valeur d’un produit de plusieurs facteurs
ne change pas lorsqu’on intervertit l’ordre des facteurs .
Pour démontrer que la valeur du produit ne change pas , il suffit de
faire voir que la valeur absolue reste le même et que le signe reste aussi le
même . Or la valeur absolue du produit est égale au produit des valeurs
absolues des facteurs ; d’après un théorème d’arithmétique , elle ne
dépend pas de l’ordre. Quand au signe , il ne dépend
que du nombres de facteurs négatifs ; le théorème est donc démontré .
Ainsi :
3 (-2) (-7) 4(- 5) = 4(- 5) 3 (-2) (-7)
Corollaire . On peut
dans un produit de plusieurs facteurs remplacer un certain nombre d’entre eux
par leur produit effectué.
3 (-2) (-7) 4(- 5) = 10 12(-7) = 120 (-7) = -840
Propriété distributive de la multiplication.
Théorème :
Pour multiplier une
somme par un nombre , il suffit de multiplier les parties de la somme par ce nombre et d’ajouter entre eux les
résultats obtenus .
Nous nous
bornerons à vérifier l’exactitude de ce
théorème sur des exemples :
1er exemple . Soit
[2 + (-3) + (-4) + 17 ] 10
On a :
2 10 = 20 ; (-3) 10 = - 30 ; (-4) 10 = - 40 ; 17 10= 170
20 –30 –40 + 170 = 120
ou
2 + (-3) + (-4) + 17 = 12
12 10 = 120
dans les deux cas on a bien « 120 »
2ième exemple : soit
[2 + (-3) + (-4) + 17 ] (- 10
)
On a :
2 - 10 = - 20 ; (-3) - 10 = + 30 ;
(-4) -10 = + 40 ; 17 - 10= -170
-20 + 30 + 40 - 170
= -120
ou
2 + (-3) + (-4) + 17 = 12
12 ( - 10) = -120
dans les deux cas on a bien « - 120 »
On obtient donc le même résultat
, soit en effectuant la somme d’abord , et la multiplication ensuite , soit en
multipliant d’abord les divers parties de la somme et en ajoutant ensuite entre eux les
résultats obtenus .
On exprime cette propriété en disant que la multiplication est
distributive par rapport à l’ addition .
Remarque : la soustraction se ramenant à l’addition , la
multiplication est aussi distributive par rapport à la soustraction . En
désignant par a ; b ; c ;
d ; des nombres positifs ou négatifs , on a :
( a – b – c – d ) n = an – bn – cn – dn
La division est l’opération inverse de la multiplication.
Diviser un nombre par un autre , c’est en trouver un troisième dont le
produit par le second soit égal au premier .
Exemples :
15 : (-5 )
= -3 car (-3) ( - 5 ) = 15
-15 : (-5 ) = 3
car (+ 3) ( - 5 ) = - 15
-15 : ( 5 ) = -3
car (-3) ( 5 ) = - 15
La règle de la division est une conséquence immédiate de la règle de la
multiplication.
Le quotient de deux nombres a pour valeur absolue le quotient de leurs
valeurs absolues.
Ce quotient est positif ou négatif selon que ces deux nombres sont de
même signe ou de signes contraires.
Exemples : ( - 42 ) :
(-6) = 7
( - 21 ) : 3 = -7
21 : ( - 3 ) = -7
|
LES FRACTIONS ALGEBRIQUES |
Définition .
En algèbre , on appelle « fraction » le quotient indiqué de
deux nombres positifs ou négatifs .
Voici l’exemple de fractions :
; 
; 
les valeurs de
ces fractions sont d’après la règle de la division :
Théorème .
On ne change pas la valeur d’une fraction algébrique en multipliant ou
en divisant ses deux termes par un même nombre .
En effet , on ne change pas la
valeur absolue , d’après la proposition
analogue de l’arithmétique . Quant au signe , il ne change pas non plus
si l’on multiplie ou divise par un nombre négatif , car les signes des deux
termes changeant tous les deux , le signe de leur quotient reste le même .
Réduction au même dénominateur .
De la proposition précédente , on conclut qu’il
est possible de réduire plusieurs
fractions au même dénominateur par la même règle qu’en arithmétique .
Il en résulte que pour
étudier l’addition ou la soustraction des fractions , on peut se borner aux fractions qui on même dénominateur .
Addition et soustraction des
fractions :
Règle : pour ajouter ou soustraire (retrancher ) plusieurs
fractions ayant un même dénominateur , il suffit d’ajouter ou retrancher les
numérateurs et de donner au résultat le dénominateur commun
Ainsi , a ;b ;c ;d ;n étant des nombres positifs ou
négatifs ( dit aussi « relatifs » ) on a :
- 
- 
+ 
= 
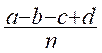
On démontre cette règle en vérifiant que la multiplication
par « n » des deux membres de l’égalité donne des résultats identiques
Règle : Le produit de deux fractions est une fraction ayant pour numérateur
le produit des numérateurs et pour dénominateur le produit des dénominateurs.
Exemples :
=
=
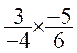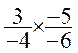On obtiendrait aisément le produit de plusieurs fractions en appliquant
la même règle :
= 
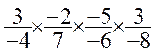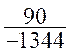
DIVISION des Fractions
|
Pour en
savoir plus ++++
|
La division est l’opération inverse de la multiplication ; la règle
s’énonce ainsi :
Règle : le quotient de deux fractions s’obtient en multipliant la
fraction dividende par la fraction diviseur renversée.
Exemples :
= 
= 
= 
= 
= 
= 
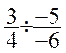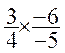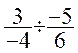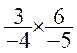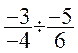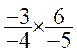La règle se justifiant en
vérifiant que le produit du quotient par le diviseur reproduit le dividende .
Remarque . dans la pratique , on calcule la valeur absolue et le signe de chaque fraction , on fixe le signe du quotient
d’ après la même règle que pour
le quotient de deux nombres
entiers ; la valeur absolue est le quotient des valeurs absolues
des fractions.
Ainsi : = =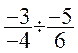
= = 
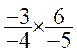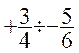TRAVAUX AUTO FORMATIFS
Donner la
règle concernant l’addition de nombres positifs et négatifs.
Donner la
règle concernant la soustraction de nombres positifs et négatifs.
Donner la
règle concernant la multiplication de nombres positifs et négatifs.
Donner la
règle concernant la division de nombres
positifs et négatifs.
Donner la
définition d’une fraction algébrique :
Donner la
règle concernant l’addition de fractions de nombres positifs et négatifs.
Donner la
règle concernant la soustraction de fractions de nombres positifs et négatifs.
Donner la
règle concernant la multiplication de fractions de nombres positifs et
négatifs.
Donner la
règle concernant la division de fractions de nombres positifs et négatifs.
Addition et soustraction des nombres positifs et négatifs :
|
Série : 1 |
|
|
4 – ( -7) + 8 |
+ 19 |
|
6 – 5 + 2 – 12 |
- 9 |
|
- 5 – 3 – ( -13 ) + ( -2 ) |
+ 3 |
Applications des nombres positifs et négatifs :
Remarque préliminaire
Nous avons donné déjà
plusieurs exemples d’application des nombres positifs et négatifs à des
problèmes concrets. C’est même de ces
exemples que nous avons pu dégager les règles de calcul .
Nous avons vérifié
que les règles d’opérations sur les nombres positifs et négatifs donnent
toujours des résultats corrects , c’est à dire « conforme à la
réalité »
Ces nombres ne sont
donc pas des abstractions pures ;
ce sont simplement des manières abrégées de représenter des faits très simples
, très élémentaires et bien connus de tous .
Il faut n’y voir
aucun mystère ; mais simplement la traduction dans le langage de l’algèbre de remarques
évidentes .
Dans les problèmes
où on utilise les nombres affectés de signes , on doit introduire des
conventions de signes bien précises , et , une fois ces conventions introduites
, s’y conformer avec beaucoup d’attention . Il ne reste plus dés lors qu’à
effectuer les opérations suivant les règles que nous avons données et à
interpréter le résultat conformément aux conventions faites .
Donnons encore quelques exemples
pour illustrer ces observations .
1°) Détermination d’un point sur un axe.
Distance de deux points .
Nous avons déjà dit ce qu’on
appelle « axe orienté »
Etant donné sur un axe la position d’un point « A », ( que l’on appelle :
abscisse d’un point ) , pour connaître la position d’un autre point
« B » , il suffit de connaître la valeur de la mesure algébrique
du segment AB ( et l’unité de longueur)
Connaissant les points « A » et « B » , pour connaître la
position d’un point « C » , il suffit de connaître ou ou
, etc.
Par exemple , sur la figure ci dessous , on a
déterminé « B », « C » , « D » en supposant le point
« A » connu , ainsi que les
segments suivants :
A D C
= 5 ; = 3 ; 
= -5
Mais cette manière de
procéder présente un inconvénient ; il est nécessaire de faire un
calcul pour connaître la position respective des points « A » et
« D » .
Il faut passer par tous
les intermédiaires .
Il est plus commode , pour fixer la position d’un point sur un
axe , de donner sa distance à un point fixe , toujours le même , qu’on appelle
« origine des abscisses » et que l’on désigne généralement par la lettre « O » . La distance
d’un point quelconque « A » au point « O » est la valeur
algébrique du segment OA ( noté : 
) , on dit que c’est l’abscisse du point « A »
Ainsi , sur la figure ci dessous , l’abscisse
du point « A » est + 3 ; l’abscisse du point
« B » est –2
B O A
Définition de l’ abscisse d’un point :
L’abscisse d’un point sur un axe est la
valeur algébrique du segment allant de
l’origine à ce point .
|
|
Problème : Etant donné es les abscisse de deux points , calculer
leur distance.
Soient A et B les eux points
donnés ; désignons par « a » et « b » , leur abscisses
, c’est à dire nous posons :
= a et 
= b
Nous voulons calculer la mesure algébrique du segment AB.
Nous avons établi à propos des segments que l’on a :
= 
+
ce qui signifie , rappelons – le : aller de A en B , équivaut à
aller d’abord de A en O , et puis de O en B.
On a d’ailleurs : AO = -
OA= - a
OB =
b
Il en résulte donc : = -a + b
= b - a
Telle est la formule qui donne la mesure algébrique de deux points .
Ce qui se traduit en langage littéral :
La mesure algébrique de deux
points A et B est égale à l’abscisse du second « B » diminué de
l’abscisse du premier « A »
Bien que cette règle , ayant été démontrée , n’ait pas besoin de
vérification , cette vérification sur des exemples n’en est pas moins
profitable au commencement .
Exemple 1 :
B O A
= a = - 3 (puisque = 3 ) ; = b = -2
= + = (-3)
+ (-2) = -5
Exemple 2
A B O
= a = 3
(puisque = - 3 ) ; = b = - 2
= + = b – a
= (-2) - (-
3) =
+ 5
Exemple 3
= a = 5
(puisque = - 5 ) ; = b = - 2
= + = b – a
= (-2) - (-
5) =
+ 3
Exemple 4
B A O
= a = 1
(puisque = - 1 ) ; = b = - 4
= + = b – a
= (- 4 ) - ( 1
) = - 3
Il ne faut pas perdre de vue que
la mesure algébrique d’un « bipoint » est positive ou négative
suivant que la direction de ce bipoint est elle-même positive ou négative .
DETERMINATION D’UN EVENEMENT dans le temps
. ORIGINE DES TEMPS . UNITE DE TEMPS
Pour déterminer la position d’un événement dans le temps , on
choisit une époque bien déterminée que
l’on appelle « origine des temps » et une « unité de
temps ».
La date de chaque événement est alors représentée par un nombre positif
si l’événement est postérieur à l’origine
des temps , négatif s’il est antérieur ,
et dont la valeur absolue est égale à la mesure de l’intervalle de temps qui sépare cet événement de
l’origine .
Prenons , par exemple , comme origine des temps le 12 janvier 1910 , à
midi , et comme unité « l’heure » .
Si divers événements se produisent : le
12 janvier à 11 heures du soir , le 13 à 8 heures du matin , le 11 à 9 heures
du soir , le 12 à 8 heures du matin , leurs époques seront respectivement
égales à +11 ; + 20 ; -15 ; - 4
.
On appelle
« époque d’un événement » l’intervalle de temps qui sépare cet
événement de l’origine des temps , affecté du signe + si l’événement est postérieur à cette origine
, et du signe « - » s’il lui est antérieur.
Intervalle qui sépare deux événements ;
Lorsque l’on connaît les époques de deux événements , A et B ,
l’intervalle de temps qui les sépare est
égal à l’époque de B diminuée de
l’époque de A.
L’ intervalle ainsi obtenu est positif
si A est antérieur à B , et négatif si A est postérieur à B , on peut le
désigner par la mesure algébrique de AB
.
Ce n’est pas autre
chose en somme que l’application au
temps de la règle des abscisses pour la
mesure algébrique de deux points .
Par exemple , l’intervalle qui sépare les deux événements dont les
époques – 13 et + 25 est : +25 – ( - 13 ) = 38
Il s’est écoulé en effet 38 heures entre le 10 janvier à 9 heures du
soir et le 12 janvier à 11 heures du matin .
REMARQUE sur la « CHRONOLOGIE »
L’origine du temps communément adoptée pour la chronologie dans les pays
chrétiens est l’époque de la naissance de Jésus-Christ ; c’est à dire que
l’on suppose qu’il est né le 1er
janvier de l’ an 1 , à minuit (nous
mettons de côté les difficultés qui
résultent de l’emploi successif des calendriers julien et grégorien , et des
années bissextiles ; nous supposons toutes les années égales pour
simplifier )
C’est cette date qui doit être désignée par zéro. Un événement qui se
produit au milieu de l'an 1 aura , si l’on prend
l’année comme unité , son époque
désignée par 
ou 0,5 ; un
événement qui s’est produit au milieu de l’an 10 aura son époque désigné
après 9,5. Il ne faut pas voir là une
contradiction ; l’origine des temps étant le moment de la naissance de J-C , l’époque 9,5 ou 9 est celle où il y a 9
ans ; il est dans sa dixième
année que l’on appelle l’an 10 . C’est ainsi que , en 1910 nous sommes dans
le XXe siècle bien qu’il ne
se soit écoulé que 19 siècles et une petite fraction de siècle depuis le
commencement de l’ère chrétienne.
Quand aux années
antérieures à la naissance de J.-C. , les chronologistes les désignent par
l’an 1 avant J.-C. , 2 avant J.-C. , etc. Aucune année n’est désignée par
zéro . Un événement qui se produit le 1er octobre de l’an 1 avant J.-C. aura son époque
désignée par 
; un événement qui se produit le 1er mai de
l’an 34 avant J.-C. , c’est à dire 33 ans et 7 mois
avant la naissance de J.-C. , aura son époque désignée par 
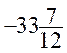l’année étant toujours
choisie comme unité .
Il est dés lors très aisé de calculer
l’intervalle de temps qui sépare deux
événements .
Exemple : un homme est né le 1er mai de l’an 12 avant
J.C. , et mort le 1er août de
l’an ‘( après J.-C.) combien de temps a-t – il vécu ?
En choisissant
l’année pour unité , l’époque de sa naissance est
-
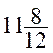et l’époque de sa mort 
;
- (-) = +
= 
= 
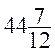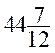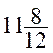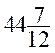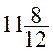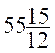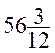
la réponse est : 56 ans 3 mois .
|
Problèmes : |
1 ° ) Un commerçant constate
qu’il doit à diverses personnes les sommes suivantes : 323,50 € ;
402,50 € ; 312,75 €.
D’autre part , divers personnes lui doivent 300 € , 250 € , 417,45 €
.Il a actuellement en caisse 1 000 € . Combien aura –t-il après ses
comptes réglés ?
2° ) Un commerçant doit à divers
personnes 3640 € ; 2350 € ; 4500 € , divers personnes lui
doivent 2000 € ; 3000€ ; et
1500 € . il a en caisse 492,50 € . Quelle est sa situation ?
3°) Jean est plus âgé de 3 mois 6 jours que Pierre et plus jeune de 6 mois et 5 jours que Franck . Quelle différence d’ âge y a t - il entre
Franck et Pierre ?