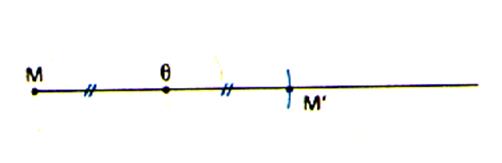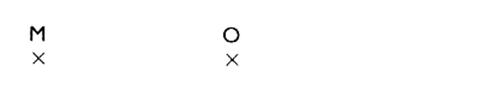|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
Niveau. VI ; V |
|
|||||||||||||||||||||||
|
Pré requis: |
|
|||||||||||||||||||||||
|
|
|
||||||||||||||||||||||
|
|
|
||||||||||||||||||||||
|
Le point |
|
||||||||||||||||||||||
|
Le cercle :et la symétrie centrale
(centre) |
|
||||||||||||||||||||||
|
ENVIRONNEMENT du
dossier: |
|
||||||||||||||||||||||
|
Objectif
précédent : |
Objectif suivant : |
tableau : |
|||||||||||||||||||||
|
DOSSIER : SYMETRIE CENTRALE N°1 |
|||||||||||||||||||||||
|
|
1.
Généralités |
|
|||||||||||||||||||||
|
|
2.
Définition |
|
|||||||||||||||||||||
|
|
3.
Propriétés |
|
|||||||||||||||||||||
|
|
4. Figures
simples
possédant un centre de symétrie:
(niveau classe 5e) |
|
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
TEST |
COURS |
Interdisciplinarité |
|
||||||||||||||||||||
|
|
|||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
1 - Généralités :
dans
« centrale » il y a « centre », le « centre » est assimilable à un « point » |
|
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
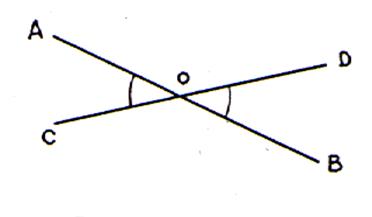
Deux points possèdent un centre de symétrie. |
|
|||||||||||||||||||||
|
|
|||||||||||||||||||||||
|
|
|
||||||||||||||||||||||
|
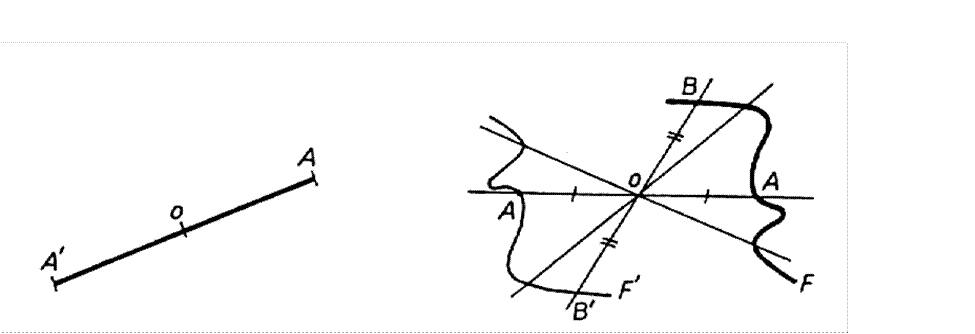
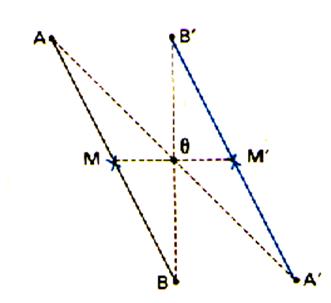
Symétrie de deux
points : Deux points A et
A' sont dits "symétriques par
rapport à un troisième point "O" , si
le troisième point "O" est
le milieu des deux points A et A' |
Symétrie d'une
courbe quelconque : Pour tracer une figure symétrique par rapport à
un centre (O) ,il
faut déterminer des points ,tracer des droites passant par un point et le
point O et reporter la même distance ( exemple OB = OB' ) |
||||||||||||||||||||||
|
|
|||||||||||||||||||||||
|
||||||||||||||||||||||||
|
|
Soit un point M et un point O donné , on appelle
symétrie centrale de centre O l’application du plan P dans le plan P qui associe à tout point ( M ) le point (
M’) tel que O soit le milieu du segment
MM’ . Notation : So : P ® P M
a M’ |
O = milieu [MM’]
( voir
la symétrie de deux nombres relatifs opposés
) |
|
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|||||||||||||||||||||||
|
|
|||||||||||||||||||||||
|
L’image du point ( M’) se
trouve à l’intersection de la droite ( q M) et de l’arc de cercle de centre q de rayon R =q M |
|
|
|||||||||||||||||||||
|
|
|||||||||||||||||||||||
|
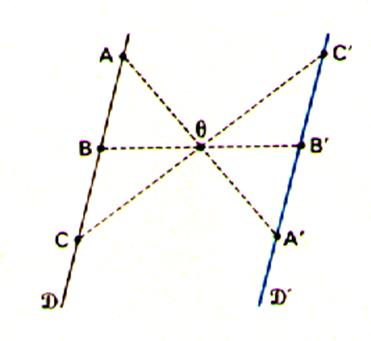
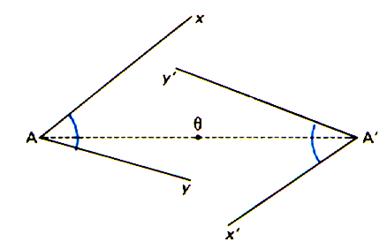
Symétrie centrale d’une droite : ( voir :info
++ : image d’une droite dans une
symétrie centrale ) |
|
||||||||||||||||||||||
|
L’image
d’une droite D est une droite D’ telle que D et D’ soient parallèles. Une
symétrie centrale conserve l’alignement. ( aussi peut-on y
voir une rotation de 180 ° autour de q) |
|
|
|||||||||||||||||||||
|
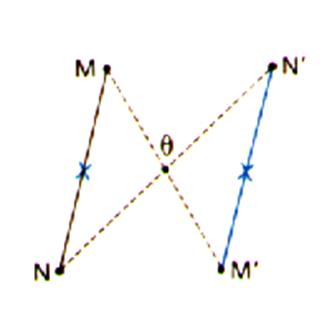
Symétrie centrale d’une distance : |
|
||||||||||||||||||||||
|
Une
symétrie centrale conserve les
distances. Exemple :
d ( N,M ) =
d( M’, N) |
|
|
|||||||||||||||||||||
|
Symétrie centrale du milieu : |
|
||||||||||||||||||||||
|
L’image
du milieu d’un segment est le milieu du segment - image. Si
M est le milieu du segment AB , alors M’ est le milieu du segment A’B’ |
|
|
|||||||||||||||||||||
|
|
|||||||||||||||||||||||
|
|
|
||||||||||||||||||||||
|
Cas particulier : le point « A » , |
|||
|
|
|||
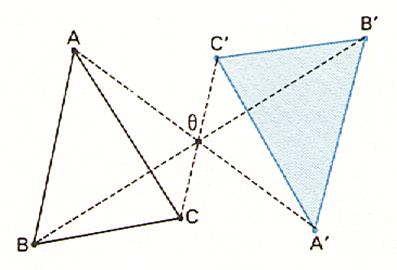
Figure : Symétrie centrale d’un triangle
|
|||
|
L’image
d’un triangle est un triangle de mêmes
dimensions (
isométrique) |
|
||
Figure : Symétrie centrale d’un quadrilatère
|
|||
|
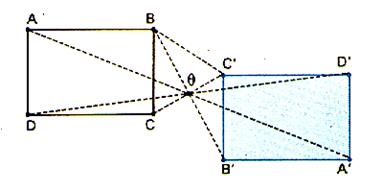
L’image d’un rectangle est
un rectangle de mêmes dimensions ( isométriques) |
|
||
|
Figure :
cercle ;
Symétrie centrale d’un disque |
|||
|
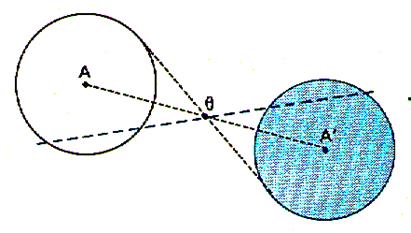
L’image
d’un cercle est un cercle de même rayon . L’image
d’un disque est un disque de même rayon . |
|
||
|
|
Conclusions :
retenons Une symétrie centrale conserve
l’alignement ; les longueurs et les angles . Une symétrie centrale conservant l’alignement ; les longueurs et les angles , il en
résulte que toute figure ( cercle ; triangle , quadrilatère ) à pour image une figure du même type et de mêmes dimensions , donc de même aire
. IMPORTANT :
Une symétrie centrale conserve les aires . |
|
|
|
|
|
||
|
|
|||
|
|
|||
|
4 - Le centre de symétrie : Figures géométriques admettant et
possédant un centre de symétrie . |
|||
|
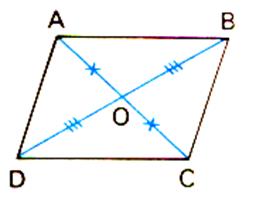
Le parallélogramme admet un centre de symétrie
, c’est le point d’intersection des diagonales . |
|
||
|
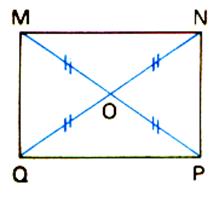
Le rectangle admet un centre de symétrie , c’est le point
d’intersection des diagonales |
|
||
|
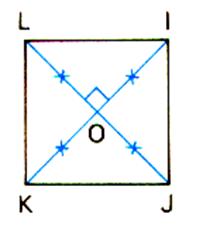
Le carré admet un centre de symétrie
, c’est le point d’intersection des diagonales |
|
||
|
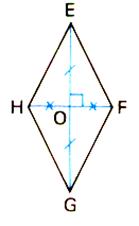
Le
losange admet un centre de symétrie , c’est le point d’intersection des diagonales |
|
||
|
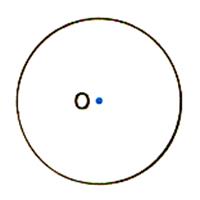
Le
cercle
admet un centre de symétrie, son centre. (toutes droites diamétrales sont axes de symétrie) |
|
||||||
|
Informations en complément sur le polygone : |
|||||||
|
Le cercle et le polygone régulier |
Quand le nombre des cotés est pair , le
centre du polygone est un centre de symétrie |
||||||
|
|
|||||||
|
NOTA: |
|||||||
|
Une
figure plane qui a deux axes de symétrie perpendiculaires, a aussi un centre
de symétrie qui est le point d'intersection de ces deux axes: |
|
|||||
|
Exemple: |
|
|||||
|
|
|
|||||
|
|
|
|||||
|
|
|
|||||
|
|
|
|||||
|
L'homme
souvent copie la nature .pour rendre plus agréable à l'œil et plus harmonieux ce qu'il bâtit. La nature nous
donne de nombreux exemples de symétrie
centrale: |
|
|||||
Les
cristaux se neige vus au microscope
|
|
||||||
|
La
marguerite (voir) |
|
||||||
|
Le
tournesol (voir) |
|
||||||
|
L'orange ,le citron que nous
coupons en deux |
|
||||||
|
A vous de trouver
d'autres exemples!!!!! |
|||||||
|
Applications
: motifs architecturaux tels les "quatre feuilles" |
|||||||
|
|
|
||||||
|
|
|||||||
|
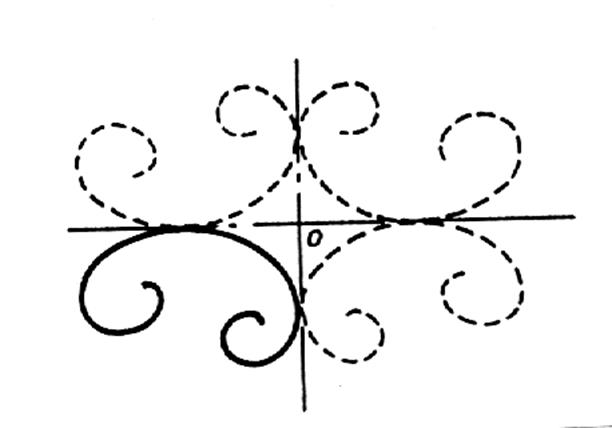
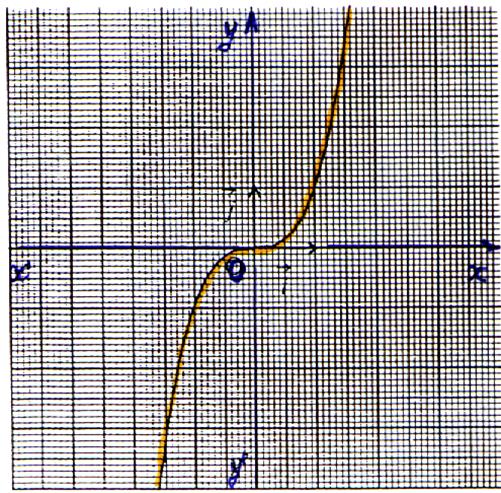
Appliquer
aux études de fonctions : Exemple :
si l’on observe le tracé de « x3 » ; on constate que « O » est centre de
symétrie
|
|
||||||
|
|
|||||||
|
|
|||||||
TRAVAUX AUTO –FORMATIF .
|
|||||||
CONTROLE
1°) Qu’appelle-t-on :
symétrie centrale ?
2°)
Traduire la notation suivante : Notation : So :
P ® P M
a
M’ | O = milieu [MM’]
3°)
Que conserve une symétrie centrale ? . 4°) Quelles sont les figures qui admettent un centre de
symétrie ? 5°)Compléter la phrase
suivante : ( 5e) le parallélogramme ; le rectangle ; le
carré ; le losange admettent un centre de symétrie qui est le point
…………….. 6°)
Le cercle admet un pour centre de
symétrie …… …………….. |
|||||||
EVALUATION
|
|||||||
|
SERIE
1 : 1°)
construire le symétrique de M par rapport à "O" |
|||||||
|
|
|||||||
|
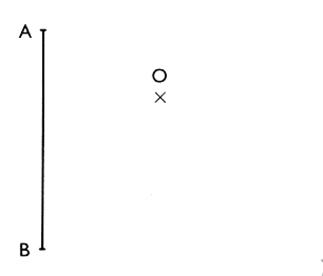
2°)
construire le symétrique du segment AB
par rapport à "O" |
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
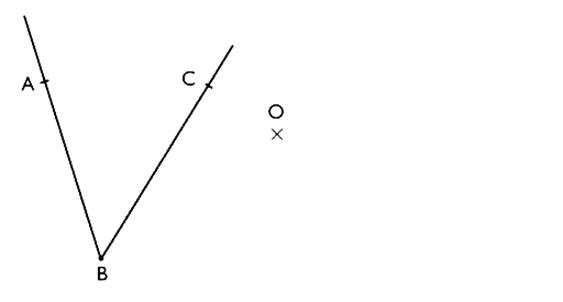
3°)
Construire le symétrique de
l'angle par rapport à
"O" |
|||||||
|
|
|||||||
|
4°)
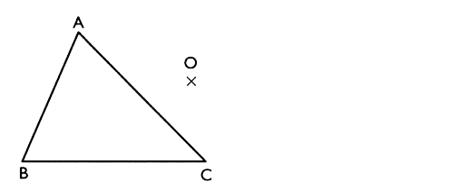
construire le symétrique du polygone ( triangle) par rapport à "O" |
|||||||
|
|
|||||||
|
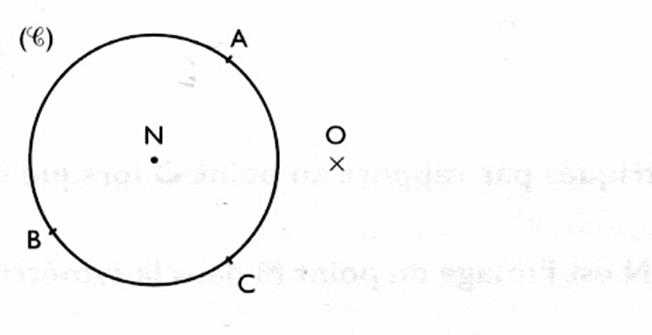
5°)
construire le symétrique du cercle
par rapport à "O" |
|||||||
|
|
|||||||
|
|
|
||||||
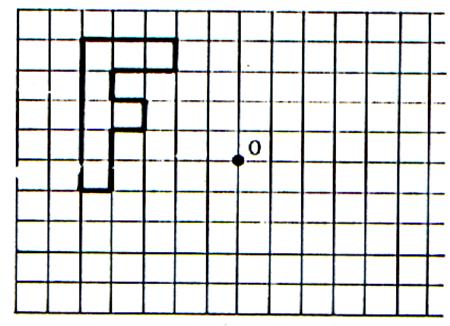
Exercice N°1
|
En
utilisant le quadrillage , dessiner l’image de la
lettre « F » dans la symétrie centrale de centre O. |
||||||
|
|
|||||||
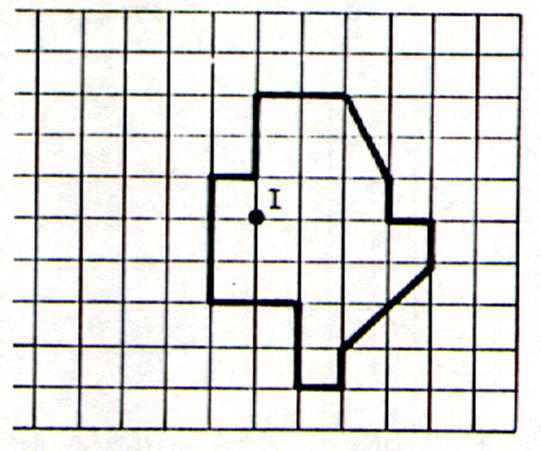
Exercice N°2
|
En
utilisant le quadrillage , dessiner l’image de la
figure ci contre et reproduire son image dans la symétrie centrale de centre I. |
|
|
|
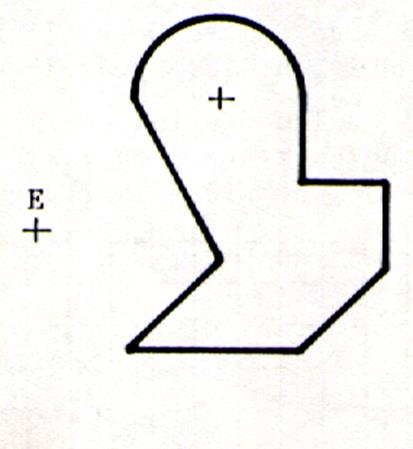
Exercice N°3
|
Dessiner avec la
règle et le compas la symétrie de la figure ci-contre de centre E |
|
|
|
|
|
|
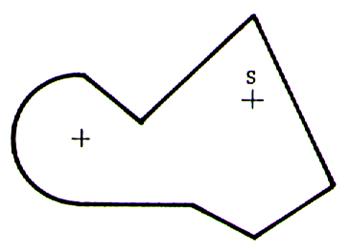
Exercice
N°4 |
Dessiner avec la
règle et le compas la symétrie de la figure ci-contre de centre S |
|
|
|
|
|