C’est un figure remarquable : quadrilatère ; le carré à 4 côtés , 4 sommets ;4 angles … parallélogramme ; ses côtés sont parallèles deux à deux ….rectangle , ses angles sont droits , ses côtés perpendiculaires …..ses côtés sont égaux : c’est un losange .

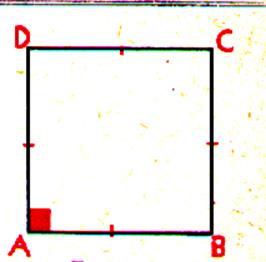
Définition

Le carré est un parallélogramme dont deux cotés consécutifs sont égaux et perpendiculaires .

Il en résulte de cette définition que le carré possède à la fois les propriétés du rectangle et celles du losange.

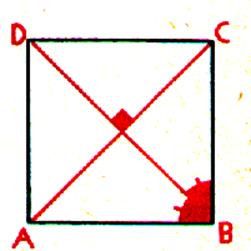
Conséquence: les diagonales du carré sont perpendiculaires en leur milieu et sont bissectrices des angles du carré.

Remarque :

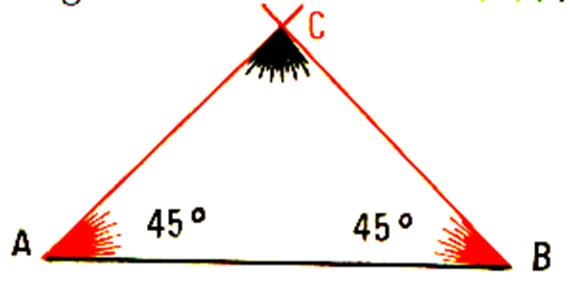
La diagonale d’un carré coupe le carré en deux triangles isocèles

car1

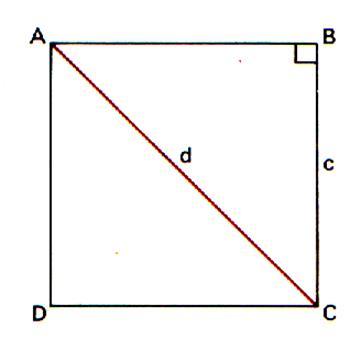
La diagonale ( d ) à pour longueur :

d = c

d =

Dans les calculs courant on prend

Exemple de calcul :

Un carré à son côté qui mesure 5 cm . Calculer la longueur de sa diagonale :

Réponse : d = 1, 414 fois 5 ; d = 7,07 cm

Vérifier ce résultat en traçant ce carré et mesurez la longueur de la diagonle…..

Pour le Calcul de la longueur de « d » Voir Pythagore

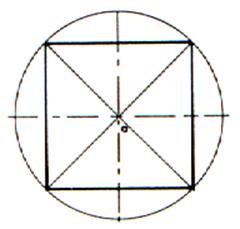
Les différents tracés du carré : en déduire les procédures de tracés.

A partir du cercle circonscrit
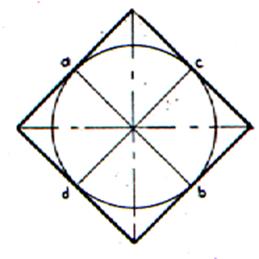
A partir du cercle inscrit.
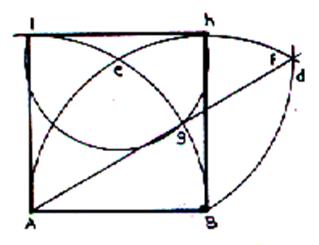
A partir d’un coté .

RESUME :

Définitions :

Rectangle ayant deux côtés consécutifs isométriques (1)

Losange ayant un angle droit (2)

AB = BC = CD= DB = a

= = = = 90°

le carré est un polygone régulier .

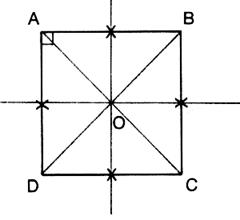
Propriétés :

- ce sont les propriétés du rectangle et du losange ;

- 4 axes de symétrie : les 2 du rectangle et les 2 du losange

- 1 centre de symétrie : c’est le point de concours des axes de symétrie (voir + : la symétrie centrale)

- (la mesure des diagonales = d = a )

Pour l’ Identification : utilisation de (1) ou (2) ( voir la démonstration en géométrie @)

TRAVAUX AUTO - FORMATIFS

CONTROLE :

Qu’est qu'un carré?

Quelles sont les propriétés du carré ?

EVALUATION

1°) Tracer un carré dont un coté mesure 4 cm.

2 ) Tracer un carré sachant que sa diagonale est égale à 4,5 cm

3 ) On donne un carré ABCD ayant pour coté 5 cm. Tracer à l'intérieur du carré , un quadrilatère EFGH tel que ses 4 sommets soient situés sur les cotés du carré et que l'on ait par ailleurs:

BE = BF = DG = DH = 3 cm

4) On donne un carré de 6 cm de coté . Tracer à l'intérieur de ce carré un losange ayant 5 cm de coté et tel que sa grande diagonale coïncide avec l'une des diagonales du carré.

5°) Tracer :

Carré de côté AB = 43 mm
Carré de diagonale AC = 52 mm
En plus : carré de périmètre p = 10 cm
En plus : carré d’aire A = 1225 mm²

Les quadrilatères

· Les tracés : Les différents tracés du carré : en déduire les procédures de tracés.

Pour le Calcul de la longueur de « d » Voir Pythagore

Les différents tracés du carré : en déduire les procédures de tracés.

A partir du cercle circonscrit