|
|
|
|
Collège : Classe
de 4ème |
||||||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|||||||||
|
Pré requis: |
|
||||||||||||
|
Cercle |
|||||||||||||
|
Angle |
|||||||||||||
|
ENVIRONNEMENT du dossier: |
|||||||||||||
|
Index : |
Objectif précédent : |
||||||||||||
|
Fiches sur la ROTATION
(au collège) |
|||||||||||||
|
|
Fiche 1 : Figures se correspondant par une
rotation. |
|
|||||||||||
|
|
Fiche 2 : Construction de l’image d’une
figure dans une rotation. |
|
|||||||||||
|
|
Fiche 3 : Images de figures
élémentaires par une rotation. |
|
|||||||||||
|
|
Fiche 4 : Image d’un cercle dans une
rotation |
|
|||||||||||
|
|
Fiche 5 : Utilisation de la rotation pour la
résolution de problèmes. |
|
|||||||||||
|
|
Fiche 6 : Triangle équilatéral. |
|
|||||||||||
|
|
Fiche 7 : le carré. |
|
|||||||||||
|
|
Fiche 8 : Exercice . |
|
|||||||||||
|
|
Fiche 9 : Hexagone régulier. |
|
|||||||||||
|
|
Fiche 10 : l’ Octogone
régulier. |
|
|||||||||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||
|
TEST |
COURS |
Interdisciplinarité |
|
||||||||||
|
|
Fiche 1 Figures se correspondant par une
rotation. |
|
|
|
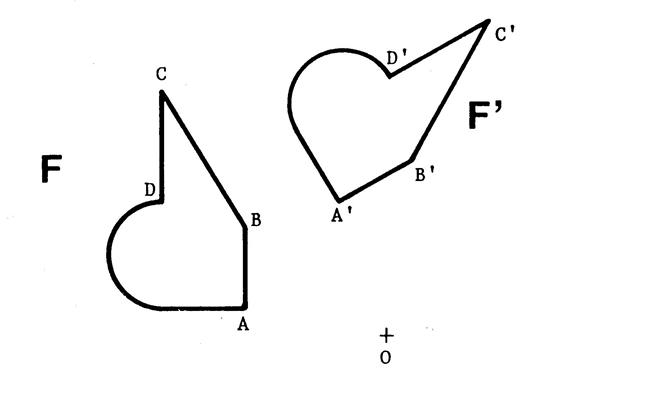
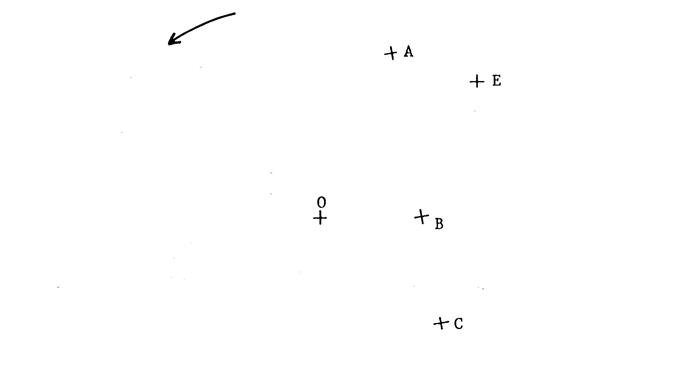
Voici ci-dessous deux figures F et F' et un point
0.
|
|
|
|
Activité : Prenez
une feuille de papier calque et calquez la figure « F » et le point
« 0 ».
|
|
|
|
Ø Pour matérialiser le déplacement de certains points
(« A » , « B » ,
« C » , « D » par
exemple), tracez les arcs de cercle
|
|
|
|
à retenir :
|
|
|
|
Etant donné, un point
« 0 » et un angle, de Tout point « M’ » de
« F’ »est obtenu à partir d’un point « M » de
« F » de telle sorte que
« OM’ = OM » et (en tournant autour de
« O » dans un sens déterminé , le même, pour i tous les points. )
|
|
|
|
Remarque : Toute figure et son image par une
rotation sont superposables |
|
|
|
|
|
|
|
Remarque
« F' » est l'image
de « F » dans la rotation de
centre 0 et d'angle 60° en tournant dans le sens des aiguilles d'une
montre.
« F » est l'image de « F' » dans la rotation ……………………………….en
tournant ………………………………………………. |
|
|
|
|
|
|
|
Activité : En utilisant le même morceau de calque que précédemment (après avoir passé au crayon gris l'envers du dessin de F), dessinez l'image
« F" » de
« F » dans la rotation de centre « O » et d'angle 130°.
( vous pouvez prendre des repères sur
la feuille pour faire tourner le calque de 130°)
|
|
|
|
|
|
||
|
|
Fiche 2 : Construction de l’image d’une
figure dans une rotation. |
|
|
|
|
|
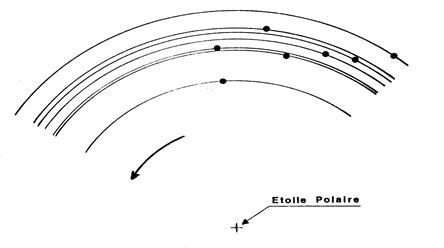
La photographie ci-contre a été prise de nuit face à
l'Etoile Polaire, en faisant une pose de
plus d'une heure. On y voit la trajectoire apparente des étoiles : il
semble que les étoiles soient animées
d'un mouvement de rotation autour de l'Etoile Polaire. (En réalité, c'est la terre qui tourne).
|
|
|
|
|
|
· Sur le dessin ci-contre, on a représenté la
Grande Ourse et une partie de la trajectoire apparente de
chacune des étoiles de cette constellation.
Ces trajectoires sont des
cercles dont le centre est l'Etoile Polaire.
· On vous demande
de dessiner la position de la
Grande Ourse 3 heures après. (le
sens de déplacement apparent est celui indiqué par la flèche).
· Commencez par
calculer l'angle de rotation. Une
étoile fait un tour complet en 24 H ,
ce qui correspond à 360°. A vous
de continuer.
|
|
|
|
|
|
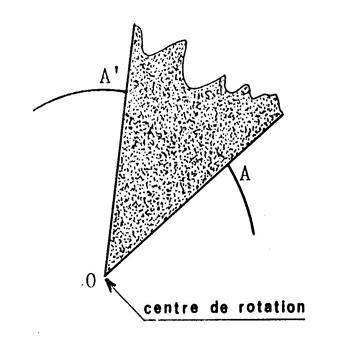
Pour placer les étoiles sur leur trajectoire, découpez dans une feuille de papier un angle de 45° et procédez comme il est
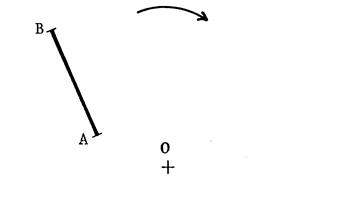
indiqué ci-contre pour la construction de « A' » image de
« A » dans la rotation de
centre « O » et d'angle 45°.
|
|
|
|
|
|
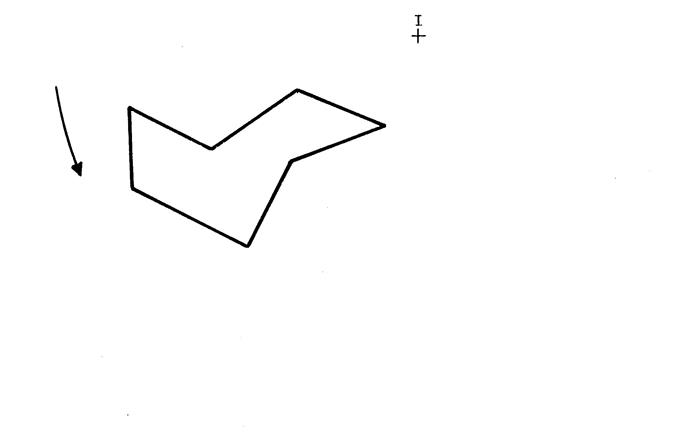
En vous inspirant de ce qui vient d'être fait construisez l'image de la figure ci-dessous dans la
rotation de centre « I » et d'angle 90° le sens de rotation est indiqué par la flèche.
|
|
||
|
|
|
|
||
|
|
|
|
|
|
|
Fiche 3 : Images de figures
élémentaires par une rotation. |
|
|
|
|
Vous avez vu
dans la fiche 1 que : Dans toute rotation, toute figure et son image sont
superposables
La figure et son image ont
donc même forme et même dimensions C'est ce que nous allons
préciser pour des figures élémentaires.
|
|
|
|
|
|
|
|
|
|
On donne un point « O »
et 3 points « A,B,C » alignés, d est la droite passant par
« A,B,C ». On considère la
rotation de centre « O » et d'angle 140° (sens donné par la
flèche). (Vous pouvez découper un
angle de 140° dans une feuille de papier).
|
|
|
|
|
Activités : |
|
|
|
|
-
Construisez les images « A',B',C' » des points « A,B,C ».Comment les points « A',B',C’ » sont-ils disposés ?
|
|
|
|
|
-
Appelons « d' » la droite passant par « A',B',C' » . Tracez cette droite.
En choisissant d'autres points
sur « d » , vous trouverez
que leur image est sur…………..
De même, tout
point de « d' » est l'image d'un
point de « d ». Donc l'image de « d » est ……….
D'une manière générale, l'image d'une droite est une
……………….. |
|
|
|
|
-
Mesurez les angles que font
entre elles « d » et « d' ». Vous trouvez ………………..et ……………………
l'un des angles est celui de la
rotation. Il est possible de le démontrer.
|
|
|
|
|
-
Mesurez [ A B ] et
[A' B’ ] puis [ BC]et [ B' C’ ]. Que constatez – vous
?................................................... D'une manière générale, l'image d'un segment est un ……………..de même ………….. |
|
|
|
|
-
Tracez la demi-droite [ BE et déterminez l'image « E' » du point
« E » . Tracez [ B 'E’ l'image de la demi-droite [ BE
est ……………………. D'une manière générale, l'image d'une demi-droite est …………………………. |
|
|
|
|
Quelle est l'image
de l'angle D'une manière générale, l'image d'un angle est un …………… de même ……………….. |
|
|
|
|
|
|
|
|
|
-
Puisque toute
surface et son image
sont superposables, elles
ont donc même aire. |
|
|
|
|
-
Vous
verrez dans la fiche 4 que
l'image d'un cercle est un ………de même …………… |
|
|
|
|
|
|
|
|
|
Théorème 31 : Dans toute
rotation (d'angle. Compris entre
0 t 180 °),
-
Des points alignés ont pour image. Des points alignés
.
-
L’ image, d'une droite et une …………………..
un des
angles déterminé par ces droites est égal à l’ angle de la rotation.
-
L’ image, d'un segment et un segment de même mesure .
-
l'image d'une
demi-droite est une demi-droite .
-
l'image d'un angle, est un angle de
même mesure.
-
'image, d'un cercle est un cercle de
même mesure.
-
Toute surface et
son image ont la même aire .
|
|
|
|
|
|
|
||
|
|
Fiche 4 : Image d’un cercle dans une
rotation |
|
|
|
|
|
On considère la rotation de centre 0 et
d'angle 110°
(sens de la flèche) .
Construisez l'image
[A'B' ]
du segment [AB ]
dans cette rotation.
|
|
||
|
|
|
|
|
|
|
|
-
Tracez le cercle « C » de diamètre [AB] et le cercle
« C’ » de diamètre [A'B'] .
En utilisant du papier
transparent, Contrôlez que « C’ » est l'image de « C » dans la rotation considérée.
|
|
||
|
|
-
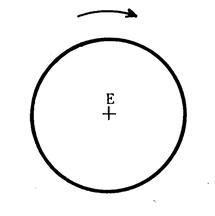
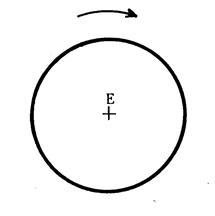
Considérons le cercle de centre E
ci-dessus à droite.
Quelle est l'image de ce cercle dans la rotation de
centre « E » , d'angle 110° ?.....................
Et si l'angle est 30° ? 120°
? 90° ?.............................................................
On dira alors : …………………………………………………………………..
|
|
||
|
|
Etant
donné un cercle, dans
toute rotation ayant pour
centre le centre du cercle, quelque soit
l'angle (et le
sens), le cercle est
sa propre image dans cette rotation,
|
|
||
|
|
|
|
|||
|
|
Fiche 5 : Utilisation de la rotation pour la
résolution de problèmes. |
|
|
||
|
|
Problème 1 : Ci-contre :« ABC » est un triangle quelconque.
Construisez extérieurement à ce triangle les carrés « ABDE » et
« ACFG ».
Démontre
que « EC = BG » et que (EC) est perpendiculaire à (BG).
|
|
|
||
|
|
Hypothèse ……………………………………………………
Conclusion
………………………………………………..
|
|
|||
|
|
Démonstration
Puisque par hypothèse
« ABDE » est un carré,
alors « AE………….AB » et
|
|
|||
|
|
On sait aussi que toute droite
a pour image une ………………………….
Un des angles formé par la
droite et son image est égal à l'angle de la rotation.
|
|
|||
|
|
|
|
|||
|
|
Problème
2
ABC est un triangle équilatéral.
D , E , F sont des points situés respectivement sur
[AB] , [BC] , [JCA] et tels
que AD = BE = CF.
Démontrez
que DEF est équilatéral.
Indication
En appelant 0 le centre du
triangle ABC, considérez une rotation de centre 0 et d'angle 120°.
|
|
|
||
|
|
|
|
|||
|
|
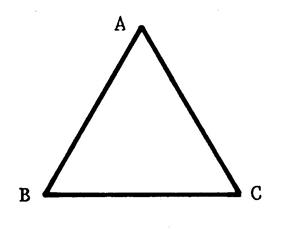
Fiche 6 : Triangle équilatéral. |
|
|||
|
|
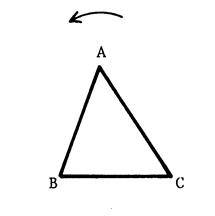
Voici un triangle équilatéral
ABC. Trace ses
axes de symétrie. Combien en a-t-il ? ……………………………..
Tracez son
cercle circonscrit. Appelons « O » le centre de ce cercle.
-
Calquez le triangle « ABC » et le point « O » , Piquez le compas en « O » et faites tourner le calque de telle sorte que le dessin du triangle s'applique exactement sur lui-même.
Vous venez
d'effectuer une rotation.
Quel est son centre
?..................................
Quel est son angle ? (calcule-le)
|
|
|
||
|
|
On dit
que cette rotation laisse invariant le triangle équilatéral . Y en a-t-il une autre ?
|
|
|||
|
|
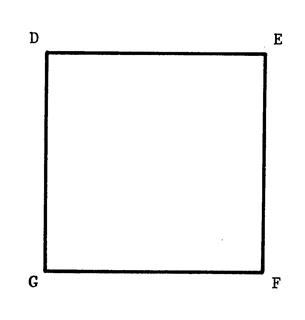
Fiche 7 : le carré. |
|
|||
|
|
Voici un carré « DEFG » .
Tracez ses axes de symétrie.
Combien en a-t-il
?....................
Tracez son cercle circonscrit.
Appelons « I » son centre.
Déterminez comme précédemment les rotations laissant invariant le
carré.
|
|
|
||
|
|
|
|
||
|
|
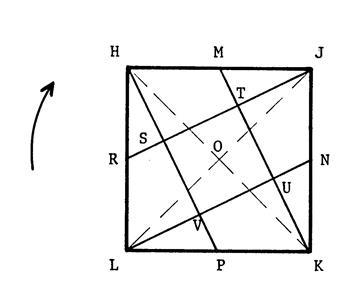
Fiche 8 : Exercice . |
|
||
|
|
« HJKL » est un carré de centre
« O » , « M,N,P,R » sont les milieux des côtés.
(HP),(JR),(KM),(LN)
se coupent en déterminant
le quadrilatère « STUV » .
Nous allons démontrer
que « STUV » est un carré .
Calquez la figure et cherche les rotations la laissant invariante. Vous avez
trouvé :…..
|
|
|
|
|
|
Considérons la rotation de centre « O »,
d'angle 90° et dont le sens est indiqué
par la flèche.
Un des côtés du
carré a pour image un autre côté du carré.
|
|
||
|
|
|
|
||
|
|
Fiche 9 : Hexagone régulier. |
|
||
|
|
Un hexagone régulier
est un polygone qui a côtés de même longueur et dont les sommets sont situés sur un
cercle dont le
rayon est égal à la longueur des côtés.
·
Vous
allez construire l'hexagone régulier inscrit
dans le cercle ci-contre :
Partant du
point A, en reportant le rayon, déterminez
les autres sommets « B,C,D,E,F » et
tracez les côtés de ce polygone.
Tracez [OA] , [OB] , [OC]
, [OD] , [OE] , [OF] .
|
|
|
|
|
|
·
Puisque OA = OB = AB = le
rayon, alors le triangle OAB est
…………………………… Donc
|
|
||
|
|
|
|
||
|
|
Fiche 10 : l’ Octogone
régulier. |
|
||
|
|
Un octogone régulier est
un polygone qui a ………….côtés de même longueur et dont les sommets sont situés sur un
cercle.
|
|
||
|
|
On vous donne
, ci-contre, un cercle de
centre « I » .
Tracez deux diamètres perpendiculaires puis tracez
les bissectrices des 4 angles que vous venez de déterminer.
Ces 8 demi-droites d'origine
« I » coupent le cercle en 8 points J,K,L,M,N,P,R, S.
[ IK est la bissectrice de
|
|
|
|
|
|
|
|
||
|
|
Fiche 11 : Constructions : |
|
|
|
|
|
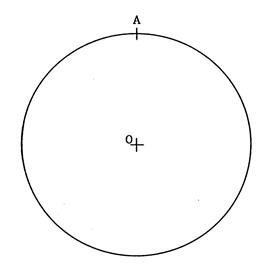
1°) Sur le
dessin de gauche , ci-dessous : Dessinez le triangle équilatéral
« ABC » dont on
donne le sommet « A » et le centre du cercle circonscrit ( vous pouvez
vous inspirer de la fiche 9 )
|
|
||
|
|
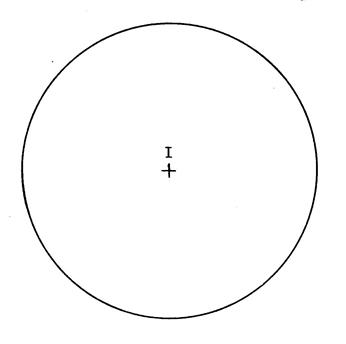
2°) Sur le dessin de droite
ci-dessous : Dessinez le carré « DEFG » dont on donne le sommet D et le centre
« I ».
|
|
||
|
|
|
|
||
|
|
Fini le
4/1/2015 |
|
||