|
POINT LIGNE PLAN |
ENVIRONNEMENT du dossier:
|
Objectif précédent les polygones |
Objectif suivant : |
DOSSIER : L’ HEXAGONE
|
|
1°) l’ HEXAGONE
régulier. (définition) |
|
|
|
|
2°) Les
3 différents tracés |
|
|
|
TEST |
COURS |
Devoir Contrôle |
Devoir évaluation |
Interdisciplinarité |
|
Corrigé évaluation |
|
|
1°) l’ HEXAGONE régulier. (définition) |
|
|
|
|
|
|
|
|
|
Un hexagone régulier est un polygone qui a ……
côtés de même longueur. Et dont les sommets sont situés sur le cercle
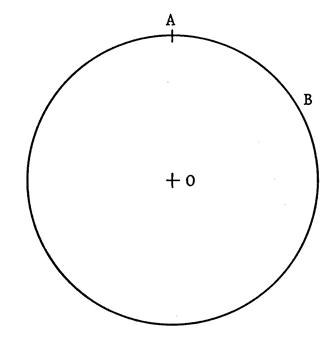
dont le rayon est égal à la longueur des côtés. Activité : On vous demande de construire l’hexagone régulier
inscrit dans le cercle ci-contre ; · Partant du point « A » , en
reportant le rayon, déterminez les autres sommets
« B », »C », »D », »E », »F »
et tracez les côtés de ce polygone. ·
Tracez : (OA) , (OB),(OC), ( OD ), ( OE ), ( OF ) |
|
|
|
|
|
|
|
|
|
Ø Puisque OA = OB = OC = le rayon, alors le triangle « OAB »
est : …équilatéral…… Donc Il en est de même pour Ø Calculez Vous en déduisez que « A »,
« O » , « D » sont …………………………………………………….. ; Expliquez ( à l’oral)
pourquoi [ AD ] , [
BE] , [CF ] sont des diamètres. Ø Calculer l’angle : Ø Calculez la somme des angles de l’hexagone régulier………………………………… |
|
|
|
|
2°) Les
3 différents tracés |
|
|
|
|
|
|
|
|
|
L’ hexagone est un polygone régulier convexe
qui à 6 cotés . Nous allons voir les 3
possibilités de tracer un hexagone. |
|
|
|
L’
hexagone (6 cotés ) |
|
|
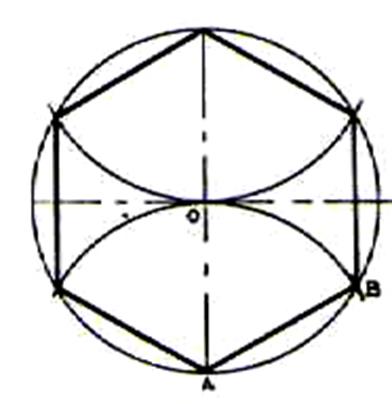
1°)
Connaissant le côté ou le cercle circonscrit |
|
|
A vous de retrouver la méthode |
|
|
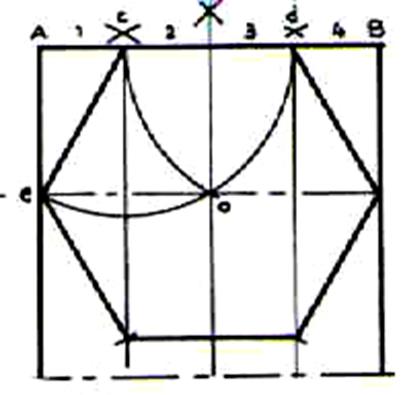
3°) Construit sur AB diamètre du cercle
circonscrit. |
|
|
|
|
|
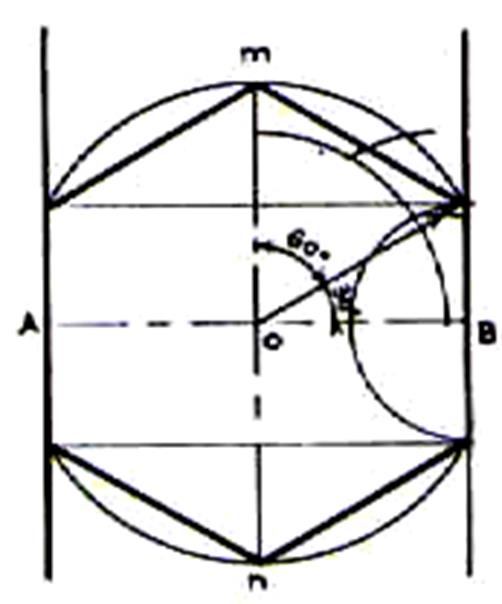
Connaissance l’apothème OB |
|
|
|
|
Qu’est
qu’un hexagone ?
EVALUATION
Tracer un
hexagone ; pas de consigne particulière .