Niveau 5

    Géométrie :  DOSSIER : Plan sous ensemble de plan / II /  Objectif cours 11

Tracer la bissectrice d’un angle

Les angles  (degré)

Index  warmaths     

Objectif précédent :

1°) traçage

Objectif suivant :

1°)Le rapporteur d’angle

tableau   

1°) angle présentation

2°) Liste des cours disponibles en géométrie plane.

DOSSIER : Les TRACES des angles à 15° , 30°;45° ;60° ;90° ;120° ;180° ;..

Construction @ d’un angle égal à un angle donné xOy

Tracé d’ un angle à 60°.

Comment obtenir  l’angle de 120° ? ( 3 solutions)

Tracé de l’ angle à 30°.

Tracé de l’angle à 15°

Tracé de l’angle à 45°

Tracé de l’angle à 90° :

Tracé de l’angle à 180° :

Tracé de l’angle à 120° :

TEST

COURS

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle 

Corrigé évaluation 

COURS

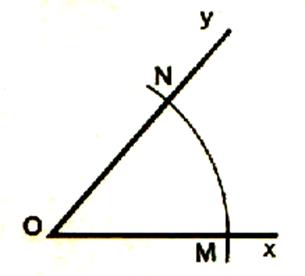
Construction @ d’un angle égal à un angle donné xOy

Avec O comme  centre et un rayon quelconque , nous traçons un arc de cercle qui rencontre les côtés de l’angle xOy en M et N

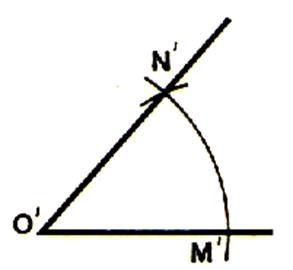
Avec un point O’ comme centre et le même rayon , nous traçons un arc de cercle.                                                                      

A partir d’un point M’ de cet arc , nous portons à l’aide du compas une corde M’N’  égale à la corde MN.

L’angle M’O’N’ est égal à l’angle xOy .

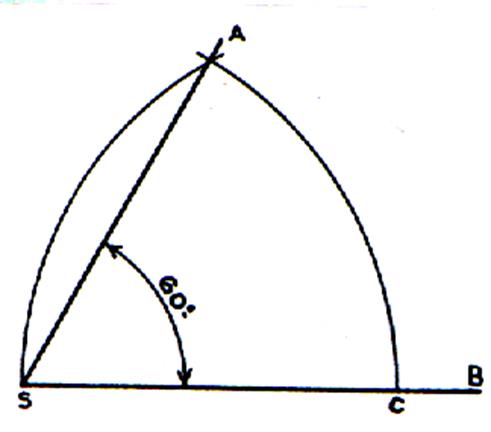
Tracé d’ un angle à 60°.

Tracer un triangle équilatéral  (figure ci contre ….)

Comment obtenir  l’angle de 120° ?

Solution 1 : utiliser le rapporteur .

Solution 2 :

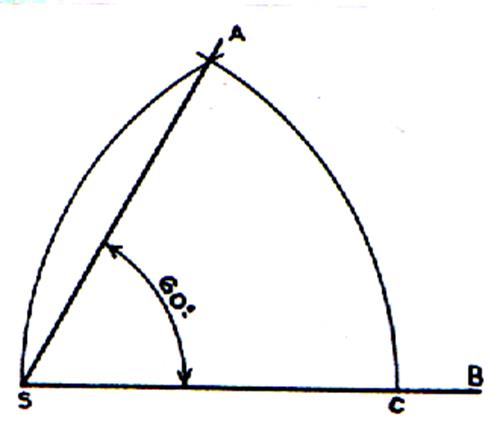
Tracer un triangle équilatéral  (figure ci contre ….)

Reproduire le tracé ci dessous.

Ensuite :

On prolonge la droite  (horizontale)  CS   (vers la gauche ) :  (on place un point C’     (symétrique centrale de  C par rapport à S .

On constate que   l’angle   C’   S   A   forme un angle de  120°

.

par  Ici  Point C’

Solution 3 :  avec le compas et la règle ..

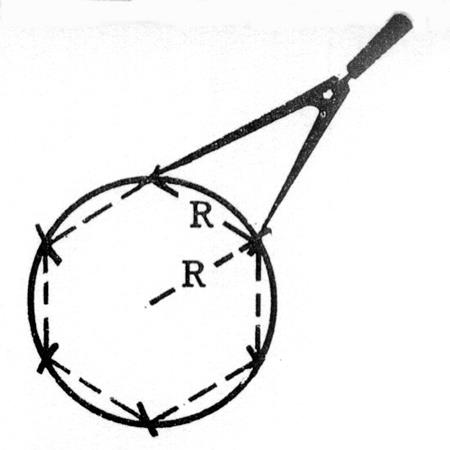
Figure 1 :   Tracer un cercle  , sans modifier l’ouverture du compas  ,diviser le cercle en 6 parties égales

Tracer une  ½ droite passant par OB  et une  ½ droite OD ; l’angle BOD mesure 120°

Placer les points  B ; O ; D

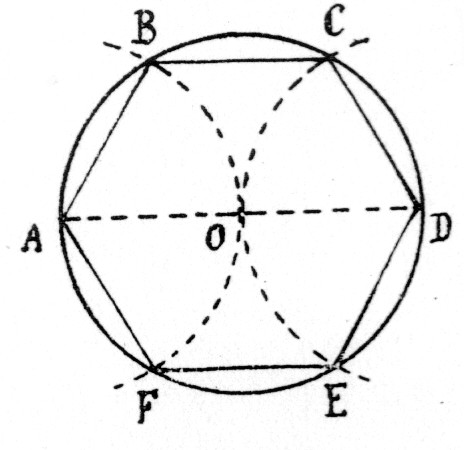
Figure 2 : vous obtenez 6 points , notés A B C D E F

La demi droite  d’origine O et passant par C est la bissectrice de l’angle  BOD .

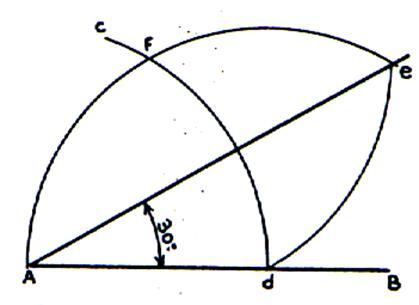
Tracé de l’ angle à 30°.

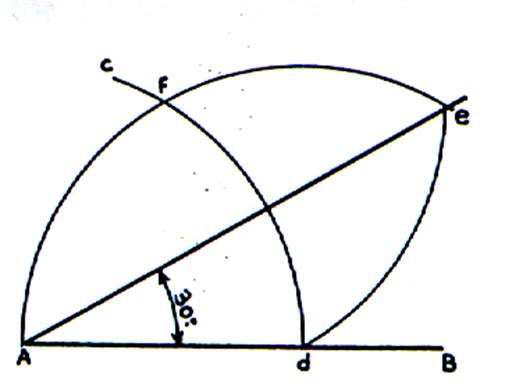
Reproduire le tracé ci dessous.

·      Tracer A  B

·      Tracer un arc de centre A passant par « d » « f » « c » ; placer la lettre « d » ; pour les tracés suivants , ne pas modifier l’ouverture du compas , puis ;

·      Tracer un arc de centre « d » passant «  A »   « f » « e » ; placer la lettre « f »

·      Tracer un arc de centre « f »  passant par « e » et « d » ; placer la lettre « e »

Tracer une demi droite d’origine A  et passant par « e »

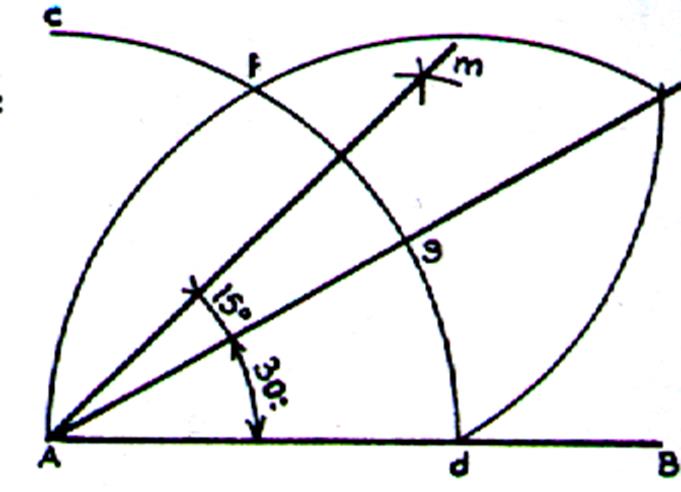
Tracé de l’angle à 15°

On trace la bissectrice de l’angle 30°.

Reproduire le tracé ci-dessous .

Tracé de l’angle à 45° :

Reproduire le tracé ci dessous.

Tracé de l’angle à 90° :

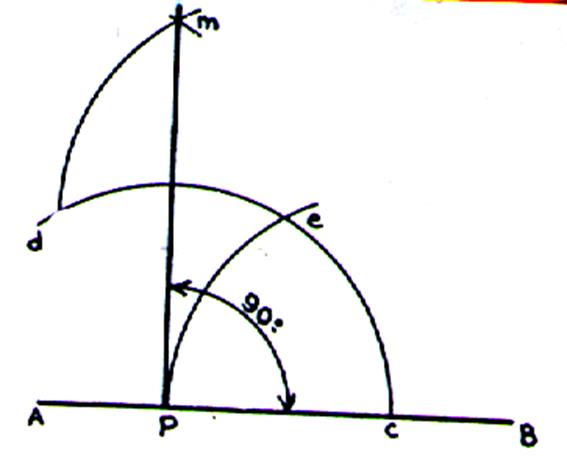
(dit aussi :  angle droit)

On obtient un angle à 90° en traçant une droite perpendiculaire à une autre droite.

Deux droites perpendiculaires forment un angle droit ( 90° ou 100 grades).

Une perpendiculaire à une droite coupent un angle plat en demi parties égales.

Reproduire le tracé ci contre.

Angle à 90°

Reproduire le tracé ci contre.

Voir les : Tracés de perpendiculaires

Tracé de l angle à 180° :

Il est appelé « angle plat » :    Tracer une droite , placer un point

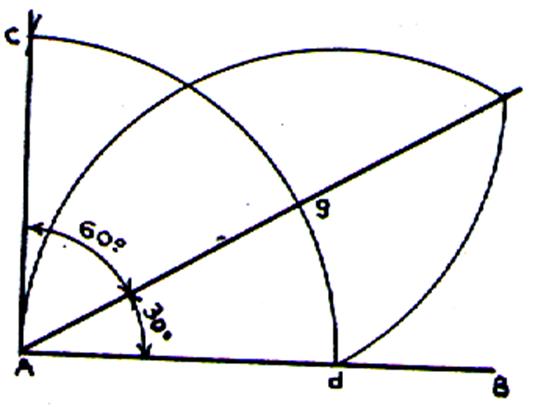
Tracé de l’angle à 120° :

Tracer la somme de deux angles : 60° + 60°   ou   la somme des  angles de  90° + 30°

Voir vidéo

TRAVAUX AUTO FORMATIFS .

CONTROLE : aucun

EVALUATION

Pour chaque tracé d’angle ; partir d’une droite AB :

1.      Tracer un angle  à 60°

2.      Tracer un angle à 30°

3.      Tracer un angle  à 15°

4.      Tracer un angle à 90°

5.      Tracer un angle à 120 °

6.      Tracer un angle à 180°

INTERDISCIPLINARITE