la perpendicularité et orthogonalité

Pré Requis:

La perpendiculaire (primaire)
Nomenclature 1
Droite

ENVIRONNEMENT du dossier:

Index : warmaths .

Objectif précédent :

Objectif suivant :

Tracés d’une perpendiculaire.

2°)Géométrie dans l’espace :l’orthogonalité

Tableau .

Liste des cours sur les « angles »

Liste des cours de géométrie

DOSSIER :

La PERPENDICULARITE ( L’ ORTHOGONALITE ) et L ‘OBLIQUE

	I ) Rappel : angle plat et angle droit.
	II ) La perpendicularité
	Notion : « perpendiculaire » et « oblique » ; « tracés »
	« orthogonalité »

TEST	COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité Perpendicularité et plan	Corrigé Contrôle	Corrigé évaluation

Info COURS:

I ) ANGLE PLAT . ANGLE DROIT :

1°) Rappels :

a) Demi – droite : construire une demi droite.

b) Angle : construire un angle

Par définition : Un angle est la figure formée par deux demi-droites qui ont même origine .

2°) Angle plat : prendre une feuille Faire un pli .Le repasser.

- Prendre un point O sur ce pli .

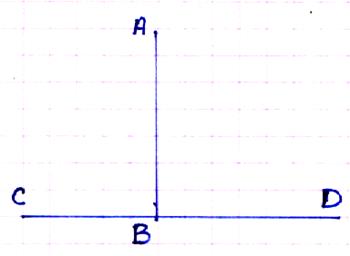
- Marquer de part et d’autre du point O le long de la droite , deux lettres A et B

Commentaire : Vous avez un angle ; est un angle qui a ses côtés dans le prolongement l’un de l’autre : c’est un angle plat . Il vaut 180 degrés ou 200 grades.

3°) Angle droit :

reprendre la feuille précédente ; faire le pli qui passe par O de telle manière que la demi-droite OA coïncide avec la demi-droite OB.

Repasser le pli . Qu’ obtient-on ?

Commentaire : on obtient quatre angles égaux qui valent chacun la moitié d’un angle plat : ce sont des angles droits.

Un angle droit vaut 90 degrés ou 100 grades .

II ) PERPENDICULAIRES

a) NOTIONS :

Activité N°1:

Pré requis : tracer un cercle

Découper un cercle . Le plier en 4 suivant des diamètres.

Marquons les plis. Ces diamètres dessinent 4 angles droits .

On dit que les diamètres sont perpendiculaires.

perpac12

La perpendiculaire est une droite qui en rencontre une autre de manière à former deux angles ( ouvertures) égaux.

Cette droite perpendiculaire ne penche , ni d’un coté ni d’un autre .

perp8

La rencontre d’une verticale AB et d’une horizontale CD forme deux lignes perpendiculaires.

Mais il ne faut pas confondre « la verticale » avec une « perpendiculaire ».

La ligne « verticale » ne peut prendre d’autre direction que celle du fil à plomb , tandis qu’une ligne perpendiculaire peut avoir toutes les directions , pourvu qu’elle fasse des angles égaux avec une autre ligne.

perp7

D

L’oblique FG est perpendiculaire à l’oblique MN.

« Oblique » :

Une droite est oblique par rapport à une autre droite si elles ont un point commun et si elles ne forment pas un angle droit.

La droite FG est oblique à la droite D

perp6

Remarque : « Droite oblique »

la droite n’est pas horizontale ,elle est inclinée d’un angle inférieur à 90°

lig2

Remarque : Deux droites perpendiculaires à une même troisième sont parallèles entre elles ;

Perpendicularité

a) « perpendicularité » : état de deux droites ou deux plans perpendiculaires.

Lignes perpendiculaires : se dit d’une ligne formant une angle droit ( 90° ; 100 grades ou radian ) avec une autre ligne .

b) Comment tracé des perpendiculaires ? ? ?

SOS cliquez ici « cours »

c) Comment montrer que deux droites sont perpendiculaires par le calcul ?.

Pour que deux droites soient perpendiculaires il faut et il suffit que leurs coefficients directeurs aient pour produit -1 .

Deux droites d'équation :

y = ax + b et y = a'x + b' seront perpendiculaires

Info plus !!!

Théorèmes :

1°) Si , d’un point , l’on mène à une même droite la perpendiculaire et une oblique , la perpendiculaire est plus courte que l’oblique .

2°)Si deux obliques issues d’un même point s’écartent inégalement du pied de la perpendiculaire , celle qui s’en écarte le plus est plus grande .

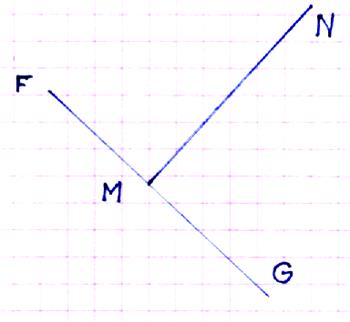
III) ORTHOGONALITE : (symbole : ^ )

Quels que soient la droite D et le point A non situé sur « D » , il existe dans le plan défini par « A » et « D » une droite D et une seule contenant le point « A » et elle est dite « orthogonale » à la droite « D » .

esp16perp

Remarque : Deux droites orthogonales coplanaires sont dites perpendiculaires.

TRAVAUX AUTO FORMATIFS.

CONTROLE :

Que signifie « droite perpendiculaire » ?

Que signifie « perpendicularité » ?

Que signifie « oblique » ?

EVALUATION :