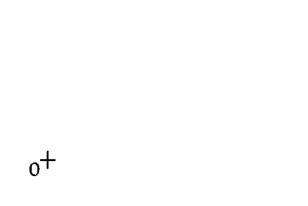Pré requis:
|
|
|
|
|
|
|
|
|
ENVIRONNEMENT du dossier:
|
|
|
|
Classe 6ème collège |
|
Objectif suivant |
DOSSIER « géométrie plane » :
Demi-plan ; angles ; Droites perpendiculaires
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Angles particuliers. ( Plat ;nul ;
plein) |
|
|
|
|
|
|
|
·
Construction de droites
parallèles ou perpendiculaires. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
·
« les Bissectrice dans un triangle ». |
|
|
|
Exercice de
tracés. |
|
|
|
|
|
|
|
|||||||
|
TEST |
COURS |
|
|||||
|
|
|
|
|
|
|
|
|
Remarque : les tracés des perpendiculaires les
plus précis se font à la règle et au compas
COURS
|
|
Plan et demi-plan. |
|
||||||||||||
|
|
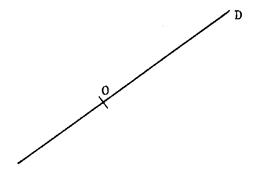
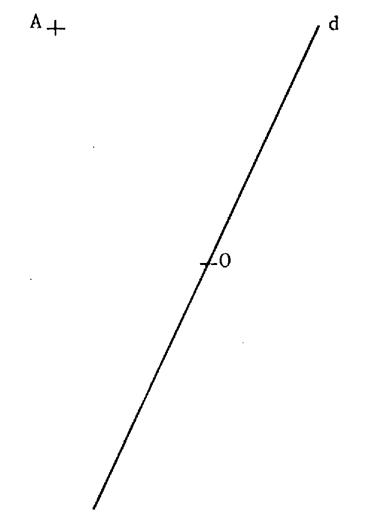
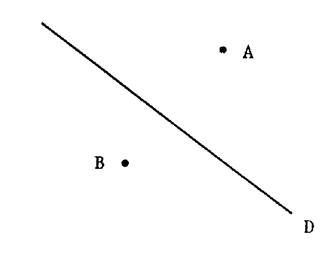
Ci contre , on a tracé
su le plan
une droite « D ». Les points situés d’une
même côté de la droite « D »d ou sur la droite « D »
constituent un ensemble que l’on appelle « demi-plan ». La droite « D » est appelée la « frontière ». La droite « D » détermine deux
demi-plans. Activité
1 : Combien une droite d’un plan détermine-t-elle de
demi plans ? Hachurer ou colorier en « bleu » le demi plan de frontière « D »
et contenant « A ». |
|
|
|||||||||||
|
|
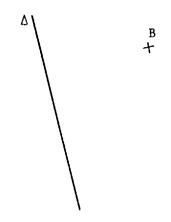
Activités 2:
« griser » ou colorier en « rouge » le demi plan de frontière « D »
et contenant « B » |
|
|
|||||||||||
|
|
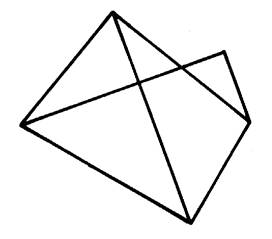
Activités 3:
Soit la figure ci contre : Combien y a-t-il de demi plans représentés sur cette figure ? |
|
|
|||||||||||
|
|
|
|
||||||||||||
|
Angle : (désignation) |
||||||||||||||
|
|
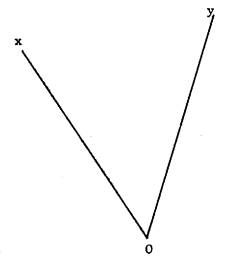
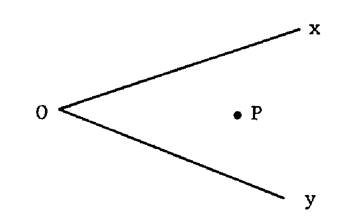
Activité
4 : - « griser » sur la
figure ci contre la portion de plan limitée par les demi droites [Ox et [ Oy et contenant le point
« P ». Remarque : on ne peut colorier qu’une partie
de cette zone ; car cette portion de plan n’est pas limitée partout. Cette portion de plan est appelée : « angle
saillant » On le note : Remarque : le
sommet de l’angle se trouve entre deux lettres ,
l’ensemble surmonté d’un « chapeau à l’endroit » . |
|
|
|||||||||||
|
|
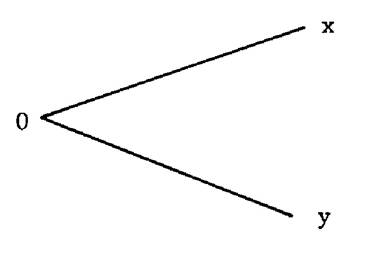
Activité
5 : Sur la figure ci contre : colorier (ou
griser) la portion de plan que vous n’avez pas grisé sur la figure
précédente. Remarque : vous ne pouvez en griser qu’une
partie. Cette portion de plan grisé est appelé :
« angle rentrant » On le note :
ou
Remarque : le
sommet de l’angle se trouve entre deux lettres ,
l’ensemble surmonté d’un « chapeau à l’envers » |
|
|
|||||||||||
|
|
|
|
||||||||||||
|
|
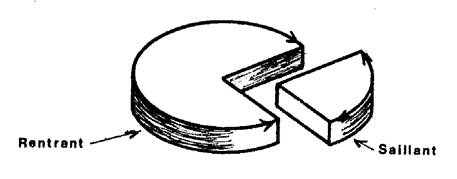
Dans les deux cas , on
remarque que « O » est le sommet de l’angle. Et Que [Ox et [ Oy sont les côtés de l’angle. Nous verrons « plus tard » que la somme
des deux angles « rentrant » et « saillant » forment un
angle de « 360° » (voir les
rapporteurs d’angles) |
|
|
|||||||||||
|
|
Désignation
d’angles : |
|
||||||||||||
|
|
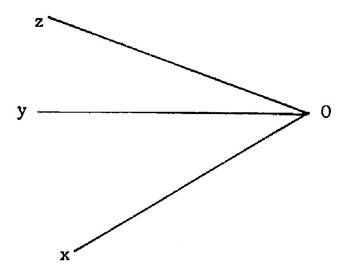
Activités 6:
Désigner (nommer) les angles de la figure ci contre : Ci-dessous :les six angles nommés , ils ont « deux à
deux » la même valeur. |
|
|
|||||||||||
|
|
|
|
|
|||||||||||
|
ou |
|
ou |
ou |
|||||||||||
|
|
|
(inverser les extrémités des lettres) |
(inverser les extrémités des lettres) |
|||||||||||
|
|
Activités 7:
|
|
||||||||||||
|
|
Pour repérer un angle sur une figure on peut
« griser » ou « colorer » la région de son sommet. Voir ci contre l’angle : |
|
|
|||||||||||
|
|
·
L’angle « grisé » ci
contre s’appelle : |
|
|
|||||||||||
|
|
|
|
||||||||||||
|
·
En suivant l’exemple précédent on
vous demande de coloriser les angles cités ci-dessous : |
||||||||||||||
|
a) Colorier en rouge l’angle : |
||||||||||||||
|
a) Colorier en bleu l’angle : |
||||||||||||||
|
a) Colorier en vert l’angle : |
||||||||||||||
|
a) Colorier en jaune l’angle : |
||||||||||||||
|
|
|
|
||||||||||||
|
|
|
|||||||||||||
|
|
Les deux côtés de l’équerre forme un angle droit. |
En utilisant l’équerre tracer ci-dessous l’angle :
|
|
|||||||||||
|
|
|
|
|
|||||||||||
|
|
|
Vous venez de tracer un angle droit …….. |
|
|||||||||||
|
|
Remarque : pour indiquer sur une figure qu’un
angle est droit, on dessine un « petit carré » : |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|||||||||||||
|
|
Considérons l’angle |
|
|
|||||||||||
|
Ses côtés sont des demi
droites :……….. [ I
u et
[ I v . Ces demi-droites sont « opposées ». Elles constituent une droite :
la droite : ……… ( u v ) Un tel angle
|
|
|||||||||||||
|
Soit la figure ci contre : Les demi droites :……….. [
Oz et
[ Ot sont « confondues ». Suivant la position du « chapeau » ;on dira que : Un angle tel que
Un angle tel que |
|
|||||||||||||
|
|
|
|
||||||||||||
|
|
||||||||||||||
|
|
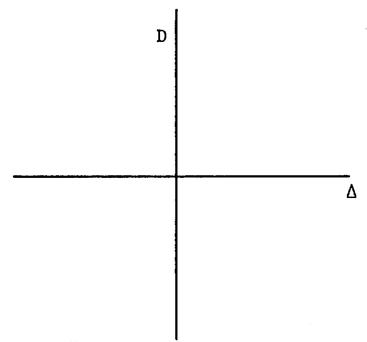
Voici ,
ci contre, deux droites sécantes « D » et «delta ( Elles déterminent entre elles 4 angles . En utilisant l’équerre ; que pouvez – vous dire
(en déduire) de ces 4 angles ? Rép. Ils ont la même forme (valeur). De telles droites sont dites « perpendiculaires » On utilise parfois le symbole : et on lit : « la
droite « D » est « perpendiculaire » à la droite delta ( |
|
|
|||||||||||
|
|
A
retenir : Deux
droites perpendiculaires sont deux droites qui déterminent entre elles
quatre angles droits. |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
Construction de droites perpendiculaires : |
|
||||||||||||
|
|
|
|
|
|||||||||||
|
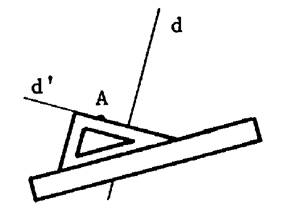
|
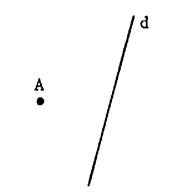
Etant donné une droite « d » et un
point « A » . En utilisant une règle et une équerre, voici
comment il est souhaitable de s’y prendre pour tracer une droite « d’ »
passant par « A » et perpendiculaire à « d ». |
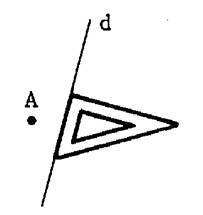
1°) Faire coïncider
un petit côté de l’équerre avec la droite « d ». |
|
|||||||||||
|
|
|
|||||||||||||
|
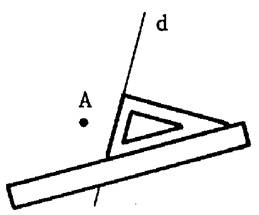
2°)
Placer la règle contre le grand côté de l’équerre. |
3°) Faire glisser l’équerre le long de la règle ( maintenir la règle, ne
pas la bouger), jusqu’à ce que le point « A » soit
sur le troisième côté de l’équerre. |
|||||||||||||
|
|
|
|||||||||||||
|
|
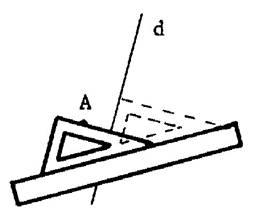
4°)Tracer une partie de la droite « d’ » (le
long du troisième côté de l’équerre.) |
5°)
Prolonger le tracer de la droite « d’ ». (suivant
les besoins) |
|
|||||||||||
|
|
|
|
|
|||||||||||
|
|
|
|
||||||||||||
|
|
Exercice :1 |
|
||||||||||||
|
|
En utilisant la procédure précédente on vous demande : |
|
||||||||||||
|
|
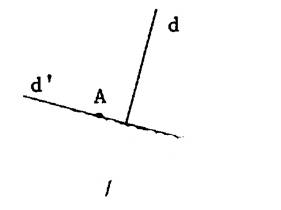
Tracer la droite «delta prime ( |
|
|
|||||||||||
|
|
Tracer la droite «D’ »
passant par « O » et perpendiculaire à «D » |
|
|
|||||||||||
|
|
Question : combien peut-on en tracer dans chacun
des ? ………………………..Une seule |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
Exercice :2 |
|
||||||||||||
|
|
Avec l’aide d’une équerre ,
trouver tous les angles droite se trouvant dans la figure ci contre. Conseil : marquer les d’un petit carré.
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
Construction de droites parallèles ou
perpendiculaires. |
|
||||||||||||
|
|
On donne un point « A », une droite « d »
et un point « O » de cette droite. |
|
||||||||||||
|
|
On demande de : |
|
||||||||||||
|
|
·
Tracer par « A » la
perpendiculaire à « d ». Elle coupe la droite « d » en « M ». |
|
||||||||||||
|
|
·
Placer sur la droite (AM) le point
« B » tel que « M » soit le milieu de[
AB ]. |
|
||||||||||||
|
|
·
Tracer par « B » la perpendiculaire
à la droite ( A B ) . Elle coupe (
A O ) en « C » . |
|
||||||||||||
|
|
·
Tracer par « O » la
perpendiculaire à « d ». Elle coupe la droite «(
B C ) en « N ». |
|
||||||||||||
|
|
·
Tracer par « A » la
perpendiculaire à la droite ( ON ) . Elle coupe la droite « ON » en «R » . |
|
||||||||||||
|
|
·
Tracer par « C » la
perpendiculaire à « d ». Elle coupe la droite « d » en « P »
et ( A R ) en
« D ». |
|
||||||||||||
|
|
Tracer ( D B ) . Si
votre dessin est bien réalisé, la droite ( D B )
passe par « O ». Sinon, effacer et recommencer .
ou tracer sur
une autre feuille. |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
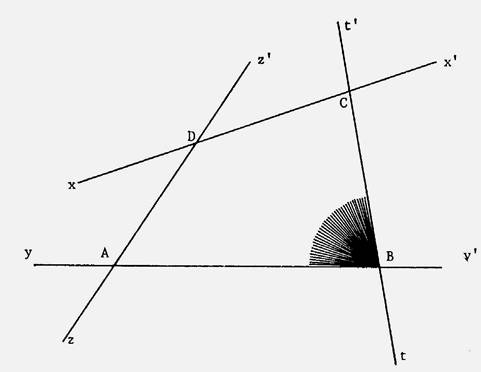
2°) D’après les instruction données pour faire la
construction , vous pouvez dire que les droites perpendiculaires à « d »
sont des droites qui on pour nom…………………………………. Que constatez vous pour ces droites ? …………………………………………………………………………………………………….. Cette constatation fait apparaître une propriété
qui est toujours vraie : |
|
||||||||||||
|
|
A
retenir : Si
des droites sont perpendiculaires à une même droite ,
alors elles sont parallèles. |
|
||||||||||||
|
|
3°) vous venez de dire que les droites ( A B ) , ( R N ) , et ( D C ) sont « parallèles » |
|
||||||||||||
|
|
Vous savez d’après l’énoncé que la droite ( A D ) est perpendiculaire à la droite ( R N ) ; Que constatez vous pour ( A
D ) et ( A B ) ainsi que pour ( AD
) et ( D C ) ?....................................................... Cette constatation fait apparaître une propriété ui est toujours vraie : |
|
||||||||||||
|
|
A
retenir :Si des droites
sont parallèles ; alors toute perpendiculaire à l’une est
perpendiculaire aux l’autres. |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
4°) Nommer toutes les droites parallèles ………………………………………………………………………. ; |
|
||||||||||||
|
|
5°) Nommer les droites perpendiculaires ;
par exemple ( A
B ) et « d » , vous écrirez : « AB ┴ d ) »
|
|
||||||||||||
|
|
6°) Nommer les points qui apparemment sont les
milieux d’un ou plusieurs segments. Exemple : M est le milieu de [ A B ] |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
||||||||||||||
|
|
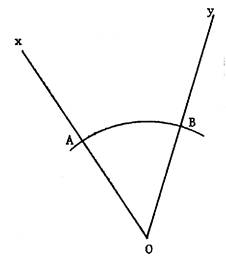
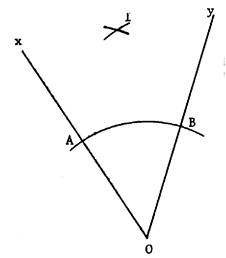
Voici ,
ci contre, un angle On
demande de tracer la bissectrice de cet angle. (avec le compas,qui
va servir à déterminer la position d’un
point par lequel doit placer une demi droite ) |
|
|
|||||||||||
|
Tracer un arc de cercle centre « O » ;
Celui-ci coupe la demi droite [ Ox en « A » Et
coupe la demi droite [ Oy en « B » |
|
|||||||||||||
|
Tracer ensuite deux arc
de cercle de même rayon qui se coupent en un point « I » |
|
|||||||||||||
|
|
Tracer ,
maintenant , la demi droite : [ Oz passant par « I »
. Cette demie droite s’appelle : la bissectrice de |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
Activité
suivante : ·
Prendre une feuille de papier et
refaite cette construction. |
|
||||||||||||
|
|
·
Plier cette feuille suivant la bissectrice : [ Oz Observations :
Que constatez vous pour les côtés
[ Ox et [ Oy ? ( elles
sont superposées) Que peut – on dire alors concernant les angles :
On remarque qu’il sont de même valeur …, ils sont superposables …
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
Suite : Tracer la bissectrice de l’angle :
|
|
|
|||||||||||
|
|
A retenir : On appelle « bissectrice »
d’un angle la demi – droite qui partage cet angle en deux angles
superposables. |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
Bissectrice d’un angle plat. |
|
||||||||||||
|
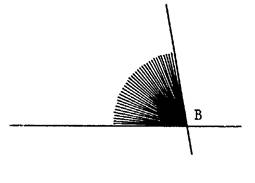
|
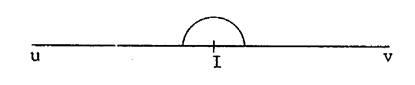
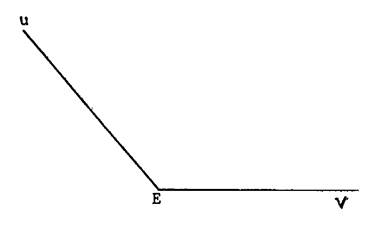
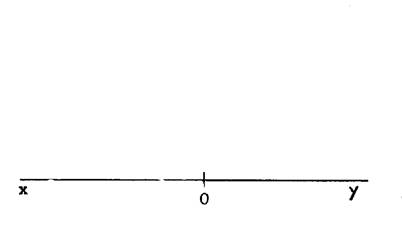
Sur la droite ci contre ,
on a placé un point « O ». ·
Comment s’appelle un angle tel que ( c’est un angle plat.) , ·
Tracer sa bissectrice :
[ Oz ; comme précédemment. ·
En utilisant votre équerre ; Que peut-on dire de Ils ont la même valeur
, ils sont droits. Donc le support de [ Oz ;
est « perpendiculaire » à «
x y » |
|
|
|||||||||||
|
|
A retenir : La bissectrice d’un angle plat partage cet angle en deux
angles droits. |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
« les Bissectrices dans un triangle ». |
|
||||||||||||
|
|
||||||||||||||
|
|
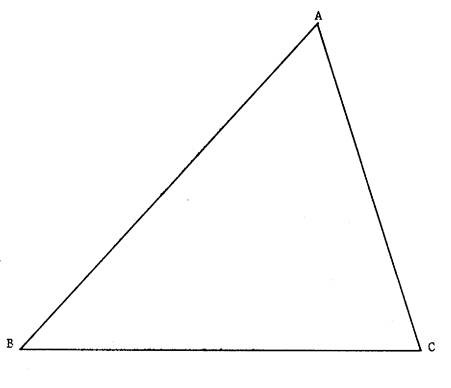
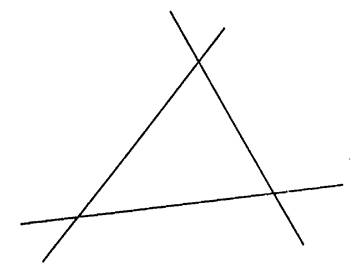
Ci contre , on vous
donne un triangle. Il détermine trois angles saillants. Nommez les :
Construire leur bissectrice. Si votre dessin est bien fait, vous devez constater
que ces trois droites se coupent en un même point. |
|
|
|||||||||||
|
|
|
|
||||||||||||
|
|
Exercices de tracés. |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
Le tracé en géométrie doit être :
fin ; net et précis. |
|
||||||||||||
|
|
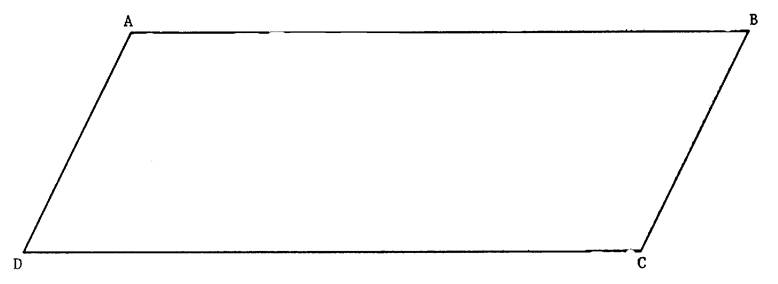
Les constructions ( arcs
de cercles ) doivent être apparentes . On vous donne ci-dessus un parallélogramme « ABCD » 1°) Tracer les bissectrices des quatre angles de « ABCD » |
|
||||||||||||
|
|
·
Les bissectrices de |
|
||||||||||||
|
|
·
Les bissectrices de |
|
||||||||||||
|
|
·
Les bissectrices de |
|
||||||||||||
|
|
·
Les bissectrices de |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
2°) Nommer les droites de la figure qui sont ( ou qui vous semblent) parallèles. Exemple : on écrira (AB) // ( D C ) . |
|
||||||||||||
|
|
3°) Nommer les droites de la figure qui sont ( ou qui vous semblent ) perpendiculaires. Exemple : on utilisera le symbole : |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
4°) En apparence, on peux dire que le
quadrilatère « EFGH » est un …………………. ( parallélogramme) |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
5°) Tracer les bissectrices des quatre angles de « EFGH » |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
Les bissectrices de |
|
||||||||||||
|
|
Les bissectrices de |
|
||||||||||||
|
|
Les bissectrices de |
|
||||||||||||
|
|
Les bissectrices de |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
6°) Nommer d’autres droites de la figure qui vous
semblent parallèles . |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
7°) Nommer d’autres droites de la figure qui vous
semblent perpendiculaires . |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
8°) Apparemment ; que pouvez vous dire sur le quadrilatère ; c’est un parallélogramme .………………………… ;
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
TRAVAUX AUTO FORMATIFS.
Revoir les « à retenir » ;
à apprendre par cœur et réciter par écrit .
Cliquez ici pour
: INFO
++++ sur le triangle rectangle «
3 ;4 ;5 » et « Pythagore »
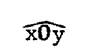
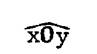
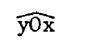
 x
x