Pré requis:

Détermination d’un plan

Notions :

ENVIRONNEMENT du dossier:

Index warmaths

Objectif précédent : La ligne droite

Objectif suivant : - les plans.

INFO+++ 1)liste des objectifs cours de géométrie plane.

DOSSIER : LE PLAN et « surface plane »

	1. Définition.
	2. Image d’un plan.
	3. « Région »
	4. Détermination du plan .(expériences)
	5. vérification ou contrôle d’un plan ou surface.
	6. Théorème.
TEST	COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité	Corrigé Contrôle	Corrigé évaluation

Info COURS

1°) Définition :

Plan : on appelle « plan » une surface qui possède les propriétés suivantes :

· 1°) Toute droite qui a deux points y est contenue toute entière.

· 2°) Par conséquent , un plan est illimité dans une infinité de direction.

· 3°) Un plan peut glisser sur lui - même d’une infinité de manières. Il peut aussi se retourner sur lui - même.

· 4°) Deux plans quelconques sont égaux, et peuvent, d’après le « 3°) », coïncider d’une double infinité de manières.

2°) Image d’un plan :

Définition du plan dans l’espace. :

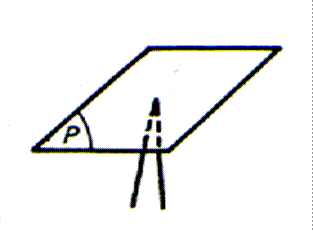
Représentation : le plan étant illimité , nous devons, pour pouvoir le dessiner, le limiter conventionnellement à un certain contour. Ce contour est en général un rectangle, qui , par un effet de perspective, est vu sous forme d’un parallélogramme.

L’image d’un plan est donné par un marbre d’ajusteur , une table de machine à usiner , une table de cuisine , ….

Une plaque rigide , en métal ou en bois , donne l’image d’une surface plane.

Soit P le plan qu’elle représente.

Remarque : représentation « graphique » d’un plan . Il se représente en géométrie par un parallélogramme ( ou comme la perspective cavalière d’un dessus de table rectangulaire )

Propriété caractéristique du plan : Toute droite qui a deux points dans un plan « y » est contenue en entier.

3° ) Régions :

Lorsque l’on abordera la géométrie dans l’espace, nous rapprocherons quelques propriétés du plan et de la droite. Et nous admettrons comme évident :
Dans l’espace et « régions » :	Dans le plan et « régions »:
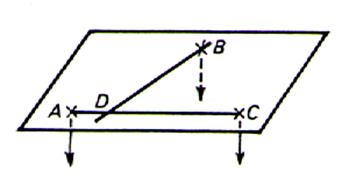
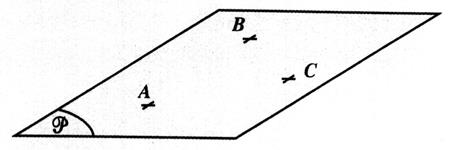
1°) Un plan partage l’espace en deux régions distinctes. Chaque région s’appelle « demi-espace ». 2°) Si on prend deux points M ,N situés dans l’une et l’autre de ces régions ( c’est à dire de part et d’autre du plan) la droite (MN) rencontre le plan en un point et un seul. On dit que la droite et le plan se coupent. 3°) Si par un point « A » du plan on fait passer une droite « xy » non contenue dans le plan, cette droite aura une partie « Ax » dans l’un des demi- espaces et le reste « A y » dans l’autre demi - espace. 4°) Deux plans peuvent glisser l’un sur l’autre de manière qu’une droite de l’un soit mise en coïncidence avec une droite de l’autre.	1°) Une droite « delta » tracée dans un plan le partage en deux régions distinctes. Chaque région s’appelle « demi- plan » 2°) Si on prend deux points M , N situés dans l’une ou l’autre de ces régions ( c’est à dire de part et d’autre de la droite « delta ») la droite (MN rencontre la droite « delta » en un point et un seul. On dit que les deux droites se coupent. 3°) Si par un point « A » de cette droite « delta », on trace dans le plan une droite « x y » distincte de « delta », la droite « x y » aura une partie , « A x »  dans l’un des demi -plans et l’autre « Ay » dans l’autre demi- plan. 4°) Deux droites peuvent glisser l’une sur l’autre de manière qu’un point de l’une soit mis en coïncidence avec un point de l’autre.

Détermination du plan :

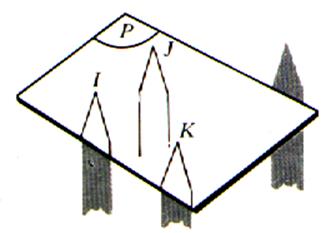
Expériences : prenons des piquets , dont les pointes sont les images des points I , J , K ,L et disposons ces piquets , de différentes longueurs , de telle sorte que trois quelconques des points I , J, K, L ne soient pas alignés.

Expérience N°1 : Par un point , il passe une infinité de plans
Expérience 1 : on peut poser la plaque d’une infinité de manières sur la pointe I .

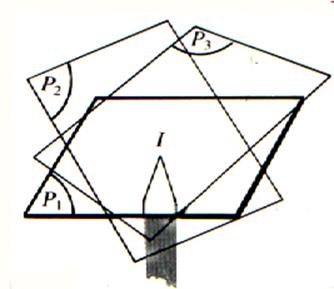
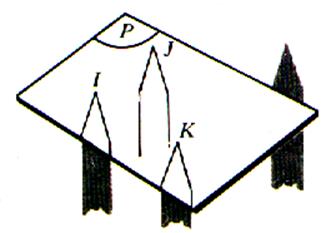
Expérience N°2 : Par deux points distincts I et J , il passe une infinité de plans.
Expérience 2 : on peut poser la plaque d’une infinité de manières , en l’appuyant sur les pointes I et J . Toutes les dispositions possibles sont obtenues en faisant pivoter la plaque autour de la droite ( I J ) Tous ces plans contiennent la droite ( I J )

Par trois points non alignés , il passe un plan et un seul
Expérience N°3 : Un plan est déterminé par trois points non alignés. Expérience 3 : on peut poser la plaque d’une seule manière en l’appuyant sur les pointes I , J et K On notera : plan ( I J K )

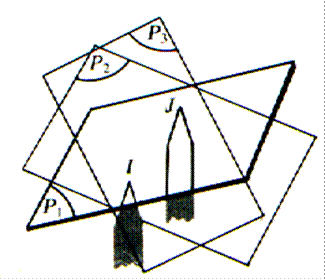
Reprenons l’expérience : lorsque la plaque repose sur les pointes I , J , K , repose – t- elle sur la pointe L ? Réponse : pas nécessairement ;elle repose sur la pointe L , si L appartient au plan déterminé par I , J et K. Si quatre points sont situés dans un même plan , on dit qu’ils sont coplanaires. Une table , une armoire est bien calée , si les quatre extrémités des pieds de la table ou de l’armoire sont coplanaires. Sinon on équilibre la table ou l’armoire en posant trois pieds au sol , on ajuste le quatrième pour que son extrémité repose sur le sol .

Vérification ou CONTROLE D’ UNE SURFACE PLANE :

En plus :

Une ligne droite sur un plan doit le toucher en tous les points , quelle que soit sa position. (voir ci dessus : la propriété d’une droite dans un plan)

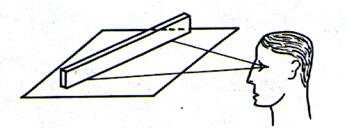
Pour vérifier qu’une surface est plane on pose contre cette surface l’arête vive d’une équerre ou d’une règle droite dans plusieurs positions. On cherche à constater la coïncidence avec un autre plan.
Constats :
Un mince filet de lumière filtre sur toute la surface : la surface est à priori plane .
La lumière passe dans le milieu : la surface est creuse .
la lumière passe sur le coté : la surface est bombée .

Si une surface n’est pas plane , on dit qu’elle est « gauche ».

Si une surface est rendue plane , on dit qu’ elle est « dressée »

APPLICATIONS :

Plan et point
Il y a une infinité de plans passant par un point donné.
Observations :
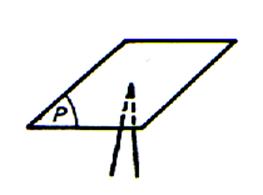
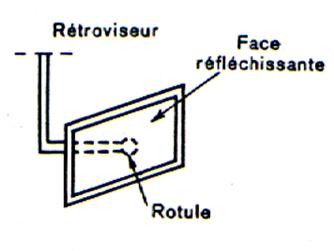
1°) On peut placer une feuille de carton rigide sur la pointe d’un compas dans une infinité de positions .	2°) Le miroir plan d’un rétroviseur d’une voiture est monté sur rotule :il peut prendre un grand nombre de position en pivotant autour d’un point grossièrement représenté par la rotule.

Plan et droite :	Voir :cylindre
On peut donc dire que : Il y a une infinité de plans passant par deux points donnés ou par une droite donnée . On sait qu’une porte peut pivoter autour de deux charnières ou d’une tringle qui les relie.

Conclusion :
Trois points non alignés déterminent un plan et un seul.
Application : Plan et les 3 Points
Tout appareil scientifique de précision doit reposer sur un plan. Ce plan est déterminé par les trois pointes de 3 vis calantes .Il est très rare que 4 points choisis au hasard se trouvent dans un même plan . (le quatrième point est réglable).

En mécanique : un plan défini par plus de 3 points est dit « hyperstatique ».

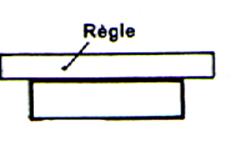
REMARQUE :

Deux droites parallèles déterminent un plan.

On sait que l’on peut poser ( appuyer ) une feuille plane de carton sur deux règles parallèles.

Théorème : Par trois points A , B , C non alignés , il ne passe qu’un seul plan.

Autrement dit : Trois points A, B , C , non en ligne déterminent un plan.

Conséquences :

· I ) Par une droite et un point extérieur , il passe un plan et un seul.

· II) Par deux droites qui se coupent , il passe un plan et un seul.

TRAVAUX AUTO - FORMATIFS.

CONTROLE:

1°) Niveau : Collège : Par combien de points (minimum ) peut-on faire passer un point ?

2°) niveau lycée : Enoncé le théorème et ses deux conséquences sur la détermination d’un plan.

EVALUATION:

1°) Niveau  : collège : Représenter par un dessin un plan .

2°) niveau lycée