Pré requis:
|
|
|
|
|
|
|
|
|
|
4. Droite |
|
Environnement du
cours :
DOSSIER :Le parallélisme et les
Droites parallèles :
|
|
I )
Définition |
|
|
|
II ) Théorèmes sur les positions relatives de
deux droites parallèles et une troisième droite. |
|
|
|
III
) Pour prouver que des droites
sont parallèles . |
|
|
|
IV
) Autre façon de le
prouver (par des activités) |
|
|
|
V) Vérifier à la règle et l'équerre le
parallélisme de deux droites.
|
|
|
|
VI) Construction… |
|
|
TEST |
Interdisciplinarité |
|
|
|
COURS: |
|
|
|
|
|
|
|
I ) PARALLELISME : « parallélisme » : état de deux droites ou deux
plans parallèles. « Lignes
parallèles » : se dit d’une ligne distante d’une autre dans toute son étendue
Ainsi : Par
définition :
Des droites parallèles sont des droites qui ne se coupent
jamais. |
|
|
Remarques : elles ne sont
pas sécantes @;
elles ont la même direction. @ |
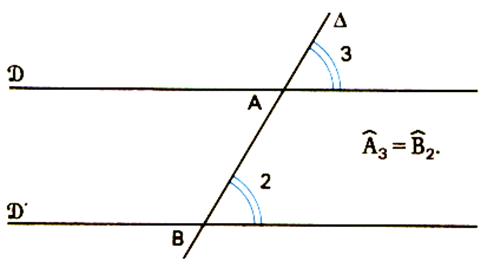
Exemple :
D et D’ sont parallèles
Ici : Informations sur le tracé des
parallèles : @
|
|
|
|
|
|
||||
|
|
|
|
||||
|
|
Remarque : Les droites sécantes ne sont pas parallèles Elles ont un seul point commun, qui est le lieu où les deux droites
se rencontrent! |
|
||||
|
|
|
|
||||
|
|
II ) Théorèmes sur les positions relatives de
deux droites parallèles et une troisième droite : |
|
||||
|
|
A
retenir : |
|
||||
|
|
Théorème1 : Si deux
droites sont parallèles , toute droite parallèle à
l’une est parallèle à l’autre |
|
||||
|
|
Théorème 2 : si deux
droites sont parallèles , toute sécante à l’une est
sécante à l’autre. |
|
||||
|
|
Théorème 3 : si deux
droites sont parallèles
, toute perpendiculaire à l’une est perpendiculaire à l’autre. |
|
||||
|
|
Il faut montrer que si deux droites sont parallèles
, elles déterminent avec toutes sécantes des angles correspondants égaux . Pratiquement il faut effectuer une mesure :
on coupe deux droites supposées
parallèles par une droite sécante et
l’on mesure les 2 angles
correspondants ,et l’on vérifie si ils sont égaux . |
|
||||
|
|
Les angles déterminés par deux secteurs angulaires situés d’un même
côté de la sécante , l’un à l’extérieur de la bande
, l’autre à l’extérieur sont égaux . Ce sont des angles
« correspondants ». Il y a quatre couples
d’angles correspondants , par exemple : |
|
||||
|
|
|
|
||||
|
|
Il y a 4 groupes de deux angles
correspondants : |
|
||||
|
|
|
|
|
|||
|
|
|
|
||||
|
|
|
|
||||
|
|
FICHE 9 : Une façon de prouver que des
droites sont parallèles. |
|
|
|||
|
|
Vous avez vu dans une leçon « les angles « fiche 6 »
)que : si deux droites sont parallèles , elles déterminent avec toute sécante des
angles correspondants égaux. |
|
||||
|
|
Inversement : on peut se poser
le problème suivant : Si deux droites déterminent avec une sécante des angles correspondants
égaux, ces deux droites sont-elles parallèles ? |
|
||||
|
|
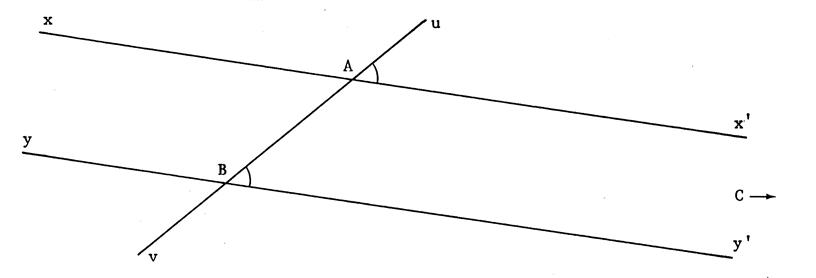
Voici , ci-dessous , deux droites « xx’ » et « y y’
» et une sécante « uv » qui les coupe en
« A » et « B ».
|
|
||||
|
|
|
|
||||
|
|
Expliquez pourquoi (oralement si possible) Puisque Vous savez que , pour deux droites d’un plan
, deux situations ( et deux seulement) sont possibles : « ou ces deux
droites sont parallèles ou elles
sont ……….. ……………. ». Supposons que « xx’ »
et « yy’ » soient sécantes. Appelons
« C » leur point d’intersection. On aurait alors un triangle « ABC » dans lequel deux angles
auraient pour somme « 180° » . ( Donc les droites « xx’ »
et « yy’ » ne peuvent être sécantes , elles sont donc …….. . ………… |
|
||||
|
|
|
|
||||
|
|
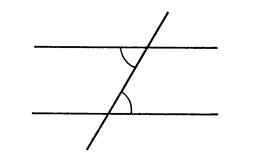
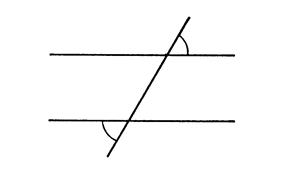
Dans les situations ci-dessous où les angles sont marqués par un arc
de cercle sont égaux . On eput affirmer que les droites sont parallèles . Expliquez pourquoi ( à l’oral ,si possible ). |
|
||||
|
|
|
|
||||
|
|
|
|
|
|||
|
|
|
A retenir : Si deux droites déterminent avec une sécante : -
ou des angles
alternes internes égaux -
ou des angles
alternes externes égaux -
ou des angles correspondants
égaux alors ces droites
sont parallèles. |
|
|
||
|
|
|
|
||||
|
|
Application : |
|
||||
|
|
Vous comprenez alors pourquoi on
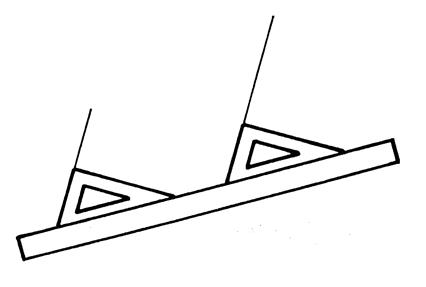
peut tracer des parallèles en utilisant une équerre et une règle Le bord de la règle matérialise
la sécante et les deux positions de l’équerre matérialisent des angles
………….. |
|
|
|||
|
|
Voir ci-dessous. |
|
||||
|
|
|
|
||||
|
|
IV) Vérifier que deux droites
sont parallèles à la règle et l'équerre . |
|
||||
|
|
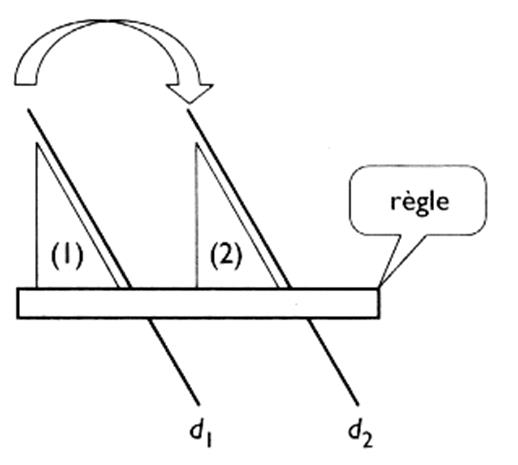
Méthode : Un bord de l'équerre coïncide avec la droite " d 1";
On fait glisser l'équerre sur la règle (qui conserve une direction fixe ) en passant de (1)
à la position ( 2). Les droites "d1" et " d2"
matérialisées par le bord de l' équerre sont
parallèles si la droite " d 2"
coïncide avec le bord de l'équerre . |
|
||||
|
|
VI) Tracé
de deux parallèles : Il y a plusieurs possibilités ,
ils sont fonctions du matériel dont on dispose : la plus simple
solution est la règle « non graduée » et l’équerre. Exemple : avec la règle
« graduée » et l’équerre
construire deux droites parallèles situées à
Solution : -
Tracer une droite ( D). -
Tracer une droite (d)
perpendiculaire à ( D) qui coupe ( D) en "H" . (
utiliser l'équerre) -
Placer sur (d) le point
"M" situé à Tracer la droite ( D') perpendiculaire à ( d
) et passant par M . |
|
||||
|
|
|
|
|
|
|
Travaux
auto- formatifs : |
|
|
|
|
Contrôle : En vous aidant du cours , compléter les
phrases suivantes : ►« parallélisme » : état de deux droites ou deux plans ………………….. ► « Lignes parallèles » : se dit d’une ligne ………….. d’une autre dans ………………………………….. Ainsi : ►Par définition :
Des droites parallèles sont des droites qui …………………………..
►Droites sécantes : Les droites sécantes ne sont pas ………………………… ►Elles ont un seul ……………………, qui est le …………………………………………… 2°) Comment peut- on montrer , pratiquement
,que deux droites sont parallèles. A retenir : collège 1°) Citer les trois théorèmes relatifs
aux positions relatives de deux
parallèles et d’une troisième droite 2°) Comment peut -on prouver que deux droites
sont parallèles ? . Construire
deux droites parallèles situées à pour cela : -
Tracer une droite ( D). -
Tracer une droite (d)
perpendiculaire à ( D) qui coupe ( D) en "H" . (
utiliser l'équerre) -
Placer sur (d) le
point "M" situé à Tracer la droite ( D')
perpendiculaire à ( d ) et passant par M . |
|