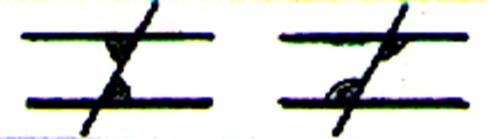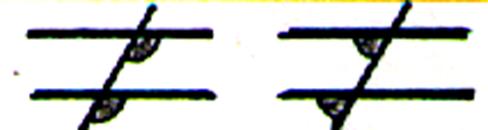Pré requis:

Les deux droites sécantes

Angles opposés par leur sommet

Positions relatives de deux droites dans un plan.(doc .plan 2 dr)

ENVIRONNEMENT du dossier:

Index : warmaths

Objectif précédent 1°)Angle 2°) positions relatives de trois droites.

Objectif suivant : 1. Le parallélogramme 2. Fiches –classe 5^ème sur les angles

Info générales : Liste des cours de géométrie. Liste des cours sur les « angles »

DOSSIER : ANGLES et DROITES PARALLELES :

Ou soit deux parallèles et une sécante.

I ) Positions relatives de deux droites parallèles et d’une troisième droite. ( les trois théorèmes)

II ) Angles déterminés par deux parallèles et une sécante .

III ) les angles « alternes » et « correspondants »

· Activités découvertes : avec un rapporteur d’angles

· 1°)Les angles alternes – internes

· 2°)Les angles alternes – externes

· 3°) Les angles correspondants

IV) résumé : Théorème.

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

COURS

I ) Positions relatives de deux droites parallèles et d’une troisième droite.

Théorème 1 : Si deux droites sont parallèles , toute parallèle à l’une est parallèle à l’autre .

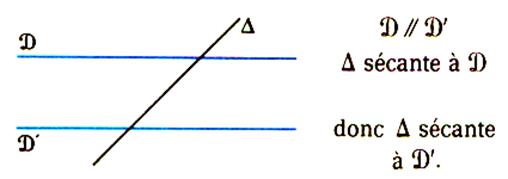
Théorème 2 : Si deux droites sont parallèles , toute sécante à l’une est sécante à l’autre .

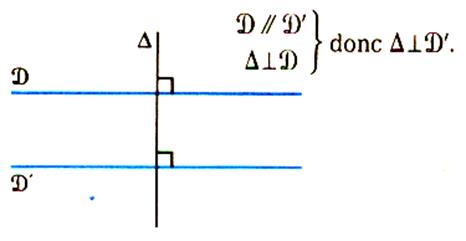
Théorème 3 : Si deux droites sont parallèles , toute perpendiculaire à l’une est perpendiculaire à l’autre .

II ) ANGLES DETERMINES PAR DEUX PARALLELES et UNE SECANTE :

Angle : Dans une représentation graphique : Deux droites sécantes qui ont pour point commun une de leur extrémité forme «  un angle » Les angles opposés sont égaux deux à deux

Parallèles coupées par une sécante
Zone interne 1 Zone interne 2 D3 Zone externe 1 Zone externe 2 D2 D D1 1 et D2 sont parallèles ; D3 coupe les deux droites .
III ) les angles « alternes » et « correspondants ».
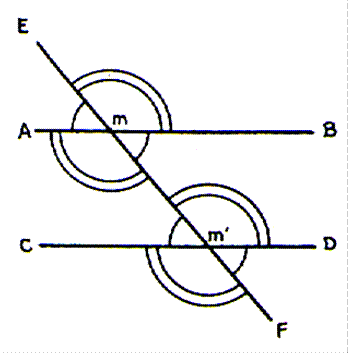
Activités : Mesurer les 8 angles ; les repérer et conclure par des égalités. ( voir ci-dessous le résumé pour construire les égalités)
=	=
=	=
=	=
=	=

DEFINITIONS : ( à retenir 5^e)

I ) ANGLES ALTERNES INTERNES

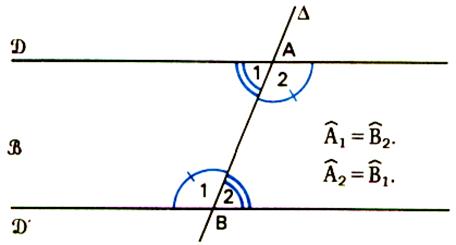
Les angles déterminés par les secteurs angulaires situés dans la région du plan limitée par les parallèles ( appelée bande « B ») et situés de part et d’autre de la sécante sont égaux .

Les secteurs sont « alternes internes »

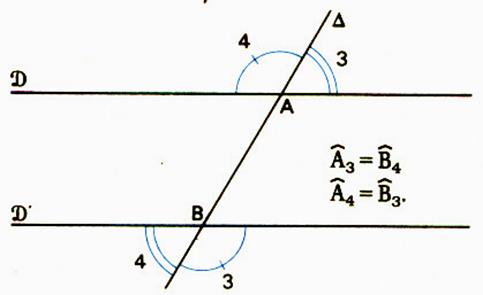
II ) ANGLES ALTERNES EXTERNES.

Les angles déterminés par les secteurs angulaires situés à l’extérieur de la bande , de part et d’autre de la sécante , sont égaux.

Ces angles sont des angles « alternes externes » .

III) ANGLES CORRESPONDANTS :

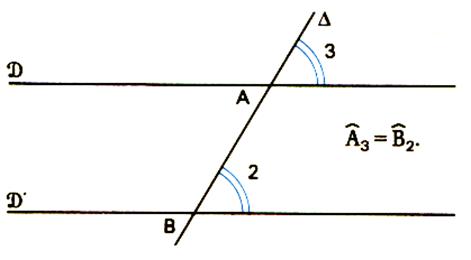
Les angles déterminés par deux secteurs angulaires situés d’un même côté de la sécante , l’un à l’extérieur de la bande , l’autre à l’extérieur sont égaux . Ce sont des angles « correspondants ».

Il y a quatre couples d’angles correspondants , par exemple : ₃ ;₂

IV) Résumé : Vocabulaire à retenir :

Les 8 angles portent un nom en fonction de leur position.
1°) Angles alternes internes
2°) Angles alternes externes
3°) Angles correspondants

Ainsi pour que deux droites soient parallèles , il faut et il suffit qu’elles forment avec une sécante :

1° ) des secteurs angulaires alternes –internes égaux ;

2° ) ou des secteurs angulaires correspondants égaux ;

3°)ou des secteurs angulaires intérieurs d’un même côté supplémentaires.

D’où le théorème :

Théorème :

Si deux parallèles sont coupées par une sécante :

Les angles correspondants sont égaux ;

Les angles alternes internes sont égaux ;

Les angles internes d’un même côté de la sécante sont supplémentaires.

TRAVAUX AUTO - FORMATIFS

CONTROLE:

Que faut-il pour que deux droites soient parallèles ?

.

Nommer les angles suivants : Angles correspondants ; Angles alternes internes ; Angles alternes externes

EVALUATION:

Tracer deux parallèles , et une droite sécante à ces deux droites : placer les 8 angles et les nommer.