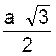CAP industriel.

Géométrie : DOSSIER : PYTHAGORE / Objectif cours 25

Pré requis:

Les racines carrées d'opérations simples
Le triangle rectangle

ENVIRONNEMENT du dossier :

INDEX warmaths

Objectif précédent : Les racines carrées pour Pythagore

Objectif suivant 1°) Présentation des travaux sur « Pythagore » 2°) cours niveau V

Tableau : présentation

DOSSIER : PYTHAGORE et sa réciproque

1°) Le Théorème

2°) La réciproque

TEST	COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité	Corrigé Contrôle	Corrigé évaluation
Test 2					CORRIGE contrôle :
		>>>Travaux auto – formatifs.		Applications :Et encore…	Autre	CORRIGE évaluation :

COURS

Rappels

« Grandeur » : on appelle grandeur tout nombre associé à une unité. ( 1 cm ; 3 m ;5,6l )

« carré » : on nomme « carré » le produit ( opération : multiplication) d’un nombre par un autre .( exemple : « a » est un nombre alors a a = a² )

Se souvenir que le plus long coté d’un triangle rectangle se nomme «  hypoténuse »

PYTHAGORE

Théorème : Dans un triangle rectangle : le « carré » de la longueur de l’hypoténuse (c’est à dire : la longueur de l’hypoténuse multipliée par la longueur de l’hypoténuse) est égal à la somme des «  carrés » des longueurs des cotés (du triangle) formant l’angle droit.

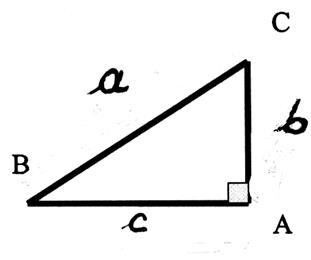
Traduction mathématique :

Se souvenir qu’il y a trois façon de nommer les cotés d’un triangle :

par un nom ( hypoténuse , coté formant l’angle droit...)

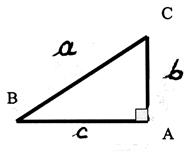
par une lettre minuscule : ( « a », « b » , ; « c »

ou en nommant les sommets des angles par une lettre majuscule et alors on désigne les cotés par les segments limités par ces points ; ( [ AB ] ; [ BC ] et [CA] ) qui ces segments se noterons par leur longueur : AB ; BC ; CD

[ BC ] lire « segment BC » ; BC lire « longueur BC »

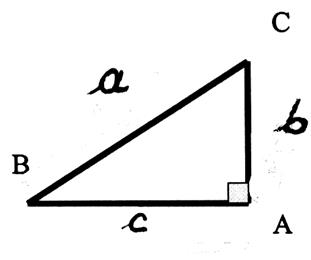
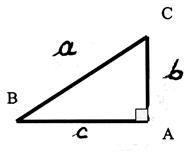
I ) si l’on nomme les cotés par des lettres. :

alors on peut écrire : aa = bb +cc ou a^2= b^2 +c^2

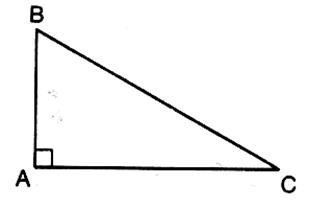
II ) si l’on nomme les sommets du triangle , par une lettre : B ; C ; A

si : BC désigne la longueur de l’hypoténuse AB désigne la longueur d’un coté formant l’angle droit AC désigne la longueur d’un coté formant l’angle droit On peut écrire , d’après « Pythagore » : BC fois BC = AB fois AB + AC fois AC soit : (BC ) ^2 = (AB) ^2+ (AC) ^2

ON PEUT demander de trouver la longueur d’ un des trois cotés : si nous appelons « x » la valeur de la longueur du coté recherché nous pouvons donc établir trois égalités différentes .( à partir d ’ une relation :c² = a² +b² ;établie à partir des données d’un triangle rectangle )

exemples :

1 - on peut calculer la longueur de l’hypoténuse à partir de si « x » = « a » alors on écrit que : x^2 = c ^2+ b^2 2- on peut rechercher « b » (inconnue « x ») * si « x » = « b » alors on écrit que : a ^2 = c ^2 + x^2 3 - on peut rechercher « c  » (inconnue « x ») * a ^2 = x^2 + b^2 *Pour le calcul avec des nombres , il faudra transformer les deux dernières égalités si l’on veut la valeur de « x »

APPLICATION DIRECTE : (aucune transformation nécessaire)

Dans ce cas on connaît la valeur des deux cotés formant l’angle droit.

Soit un triangle rectangle dont les cotés de l’angle droit mesurent l’un 30 mm , l’autre 40 mm ,calculer la longueur de son hypoténuse.

Résolution :

nous pouvons tracer la figure :

BC = x AB = 40 AC = 30 nous pouvons écrire que d’après le théorème de Pythagore : 30 30 + 4040 = xx 30 ² + 40 ² = x ² 900 + 1600 = x ^2 2500 = x ² donc x = 50 Nota : pour calculer la valeur de « x » il faut revoir l ‘objectif sur le calcul de la racine carrée d’un nombre

2°) RECIPROQUE DU THEOREME DE PYTHAGORE.

Nous admettrons la propriété suivante , qui est la réciproque du théorème de Pythagore

Si ,dans un triangle, le carré de la longueur d’un côté est égal à la somme des carrés des longueurs des deux autres côtés , alors ce triangle est rectangle .

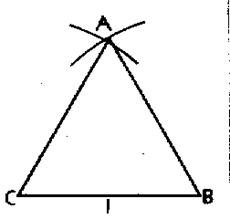
Exemple : considérons le triangle ABC dont les trois côtés mesurent respectivement :

AB = 6 ; AB² = 36

AC = 8 ; AC² = 64

BC = 10 ; BC² = 100

Nous constatons que 100 = 64 + 36

Donc que BC² = AC² + AB²

Nous en déduisons que le triangle ABC est un triangle rectangle , dont l’hypoténuse est le segment BC.

Nous pouvons dessiner le triangle rectangle !

Utilisation de la réciproque du théorème de Pythagore.

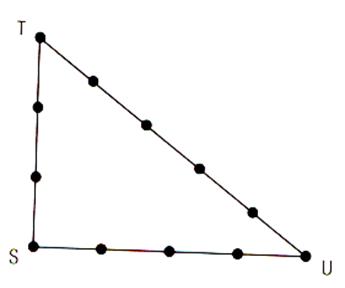
Pour tracer des angles droits , les Egyptiens se servaient d’une corde fermée à 12 nœuds , régulièrement espacés ; ou d’un segment de corde à treize nœuds (régulièrement espacés) dont un nœud à chaque extrémité . Ils la tendaient entre trois pieux de la façon , un en « T » ; un en « S » un en « U ».

On a ST = 3 ; SU = 4 ; TU = 5

D’une part : TU² = 5² = 25

et d’autre part ST² + SU² = 3² + 4² = 9 + 16 =25

On a ainsi TU² = ST² + SU² ; le triangle TSU est donc rectangle en U.

Applications particulières de Pythagore :

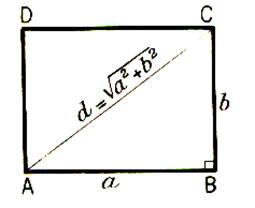
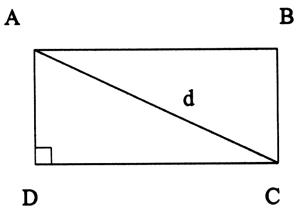
Diagonale d’un rectangle	Info plus +++

	Info plus +++
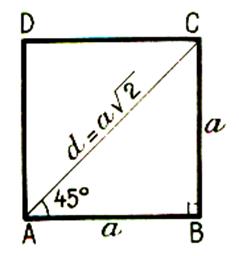
« diagonale du carré = a »
	Info plus +++
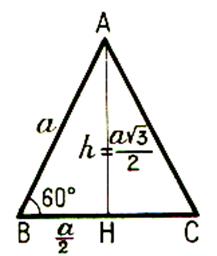
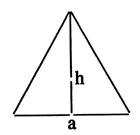
Hauteur du triangle équilatéral =

Voir les démonstrations suivantes :

Démonstrations :

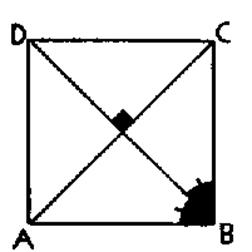
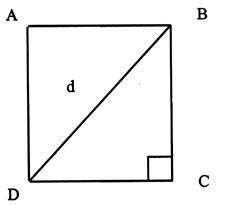
1°) diagonale du carré : considérons un carré DCBA, désignons par « a »la longueur de coté et « d » la longueur de la diagonale . Appliquons le théorème de Pythagore :au triangle rectangle DBA DB^2 = DA^2 + AB^2 DA = a ; DA^2 = aa = a^2 BA = a ; AB^2 = aa = a^2 Donc DB^2 = a^2 + a^2 = 2 a^2 D’où DB = soit DB = a On déclare que : Dans un carré , la longueur de la diagonale est égale à la longueur du côté multiplié par « racine de deux ». Remarques : - nous savons que » 1,414 - d’où d » a414 -le triangle DBA est un triangle rectangle isocèle .

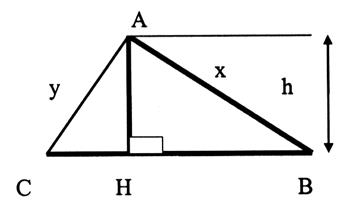
Considérons le triangle équilatéral ABC. Désignons par « a » la longueur du côté . Soit le segment AI la hauteur relative au côté [CB]. Puisque le triangle est équilatéral , nous savons que « I » est le milieu . BI ² = a² + ( a/2 ) ²

Rappels sur les calculs pouvant être utilisés avec PYTHAGORE :

Sur les racines carrées :

La racine carrée d’une somme ou d’une différence n’est pas transformable.

Traduction mathématique :

1 ) n’est pas égale à

2 ) n’est pas égale à

Pour s’en convaincre il suffit de donner une valeur à « a » et à « b » ; remplacer ces valeurs dans les expressions et comparer les résultats ( exemple prendre « a »= 5 et « b » = 3 ) .

Remarque sur le choix des valeurs « a » et « b » :

« a » doit être supérieur à « b » dans la relation «   »  ,parce que l’on ne peut pas faire la racine carrée d’un nombre négatif . = « impossible »

Il faut impérativement faire l’addition (ou la soustraction) pour pouvoir calculer la racine carrée.

A ) Soit l’égalité :

► x = a + b on peut transformer l’égalité et écrire : =

si 2500 = 1600 +900 on peut écrire : =

Calculs :

Premier membre : donne 50

Deuxième membre : , devient donne 50

B ) Soit l’égalité :

► x² = a² + b² on peut transformer l’égalité et écrire : =

(si l’on veut la valeur de « x » il faut faire la racine carrée de la somme des carrés).

si 50² = 40 ²+ 30 ² on peut écrire =

sachant que = x donc on en déduit que =50

On peut écrire que x =

Calcul de  : on ne peut pas donner directement le résultat ,il faut faire l’ensemble des opérations sous la racine, afin de n’avoir qu’un nombre , il nous sera possible alors de calculer la racine de ce nombre.

Calculs : 402 = 1600 ; 302 = 900 ; 1600+900 = 2500

^{on peut écrire l’égalité suivante :} = ; on calcule : = 50

CONTROLE :

a ) Qu ‘appelle -t- on « grandeur » ?

b) Qu’appelle- t- on « carré d’un nombre » ?

c) Comment reconnaît- on l’hypoténuse d’un triangle rectangle ?

I) Dans quelle est la condition d’application du théorème de Pythagore ?

II) Enoncer le théorème de PYTHAGORE :

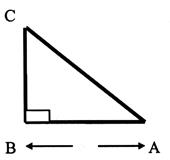
III) A partir de l’énoncé précédent mettre sous forme d’une égalité mathématique avec comme figure géométrique le triangle suivant :

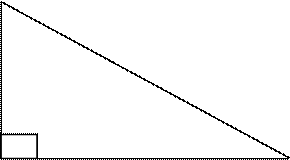
IV ) Soit l’égalité mathématique : a² = b² + c²

trouver « a = » puis « b = »  et « c = »  par transformation de l’égalité , indiquer les étapes successives.

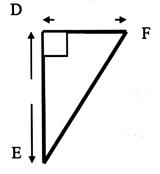
V ) Soit DF² = DC² + CF² ; trouver DF ; DC ; CF par transformation de l’égalité ( indiquer les étapes successives).

EVALUATION :

Niveau référentiel (niveau V) ( si ? SOS Cours)

Compléter le tableau

		Triangle 1	Triangle 2	Triangle 3	Triangle 4	Triangle 5
	a		37 cm		0,65 m	295 mm
	b	450 mm	35 cm	45 cm		2,36 dm
	c	600 mm		280 mm	0,33 m

Série II

N°1		Données :	Résolution  :
		BA = 108 mm
		CA = 45 mm
		Calculer :
		« a » = ?

N°2		Données :	Résolution  :
		DF = 127 mm
		DE = 156 mm
		Calculer : FE = x ; à 0,1 mm prés

N°3		Données :	Réponse :
		CA = 74 cm
		CB = 24 cm
		Calculer AB.
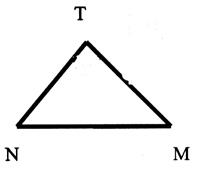
		Données :	Réponse :
		NM = 13,75 cm
		NT = 11 cm
		Calculer TM

N°5	Application : Diagonale d’un rectangle	Données :	Résolution :
		AB = 170 cm
		BC = 95 cm
		Calculer AC = « d » ( à 0,1 cm prés.)

N°6	Triangle quelconque :			Données :		Résolution :
				CB = 114 cm
				HB = 71 cm
				« h » = 83 cm
				Calculer : AB = x ( à 1 mm prés) AC = y (à 1 mm prés)
N°7	La diagonale d’un carré			Données :		Résolution
				BC = 32 dm
				En déduire la valeur de AB ; CD ; AD. Calculer BD ( = d) à 1 cm prés.
7 b ++	Etudier le cas où AB = 1 dm : d = racine de 2
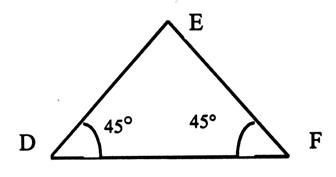
N°8	Le triangle rectangle isocèle			Données :		Réponse :
				-Calculer l’angle E : -Quelle est la nature du triangle ? -DE = 160 cm En déduire EF Calculer DF
8 b ++	Calculer DE si DF est égal à 6 cm
N°9			Données :		Réponse :
			Sachant que DC = 31 m
			CB = 33 m et BA= 56 m
			Calculer AC ( à 0,1 m prés)
N°10			Données :		Réponse :
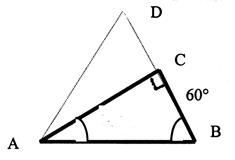
			En déduire l’angle C
			Que peut -on dire du triangle ACB , au regard du triangle ADB ?
			Quelles sont les valeurs des angles : A CB = ; D C A = ; C D A = CAD =
10 b +++		On donne AC = 60 , calculer la valeur de AB puis BC

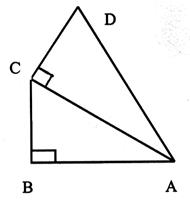
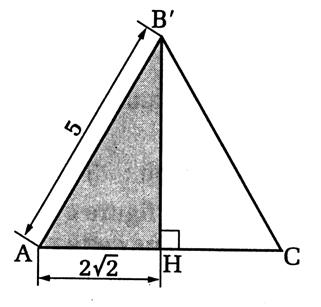
11°) Calculer B’ H : Le triangle est -il isocèle ou équilatéral ?

3°) Autres séries d'exercices

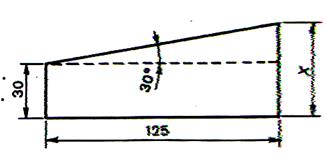
Calculer la longueur « x »

4°)

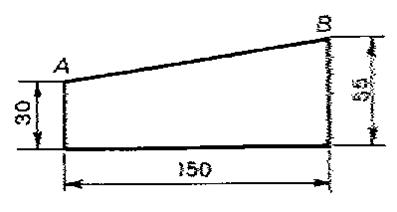
Calculer la longueur « x »

5°)

Calculer la diagonale d’un cube de 1 m d’ arête .

6°)

Calculer la diagonale d’un parallélépipède rectangle ayant pour dimensions 7 ; 8 et 10 cm .

7°)

Calculer la diagonale d’un carré de 2,5 dm de côté

8°)

Calculer la longueur de AB

9°)

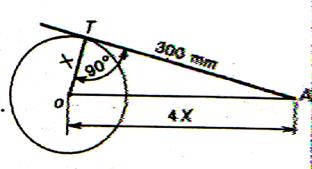
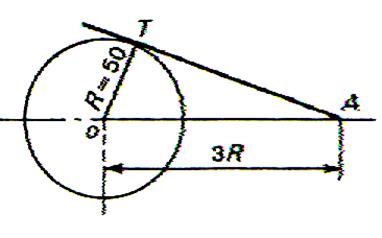
Calculer la longueur de la tangente AT (côtes en mm )

INTERDISCIPLINARITE :

Dans le bâtiment : pour effectuer un pavage dans une pièce .

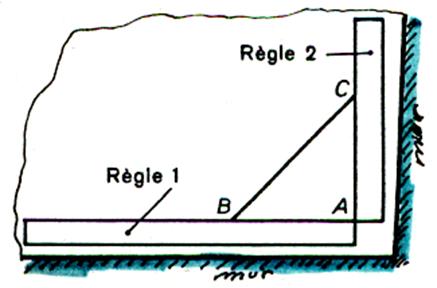
Ce procédé permettant de tracer une droite perpendiculaire par exemple pour le pavage d’une pièce. ( les murs n’étant pas eux mêmes perpendiculaires ) On mesure AB = 6O cm sur la règle 1 , qui sert de base , puis on mesure AC = 80 cm sur la règle 2 , et on déplace la règle 2 de façon que BC mesure 1m. Les deux bords AB et AC forment un angle droit.

Remarques : Sur une surface plus réduite , on pourrait porter

AB = 6 cm AC = 8 cm ; il faut que BC mesure 10 cm .

Ou AB = 3 cm AC = 4 cm ; il faut que BC mesure 5 cm .

Ou AB = 12 cm AC = 16 cm ; il faut que BC mesure 20 cm .

Voir aussi la « corde à 13 nœuds ».

PROBLEMES DIVERS :

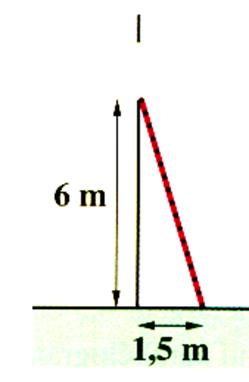
N°1 : Quelle longueur doit mesurer une échelle pour atteindre une fenêtre située à 6 m. Si on lui donne 1,5 mètres de pied ?

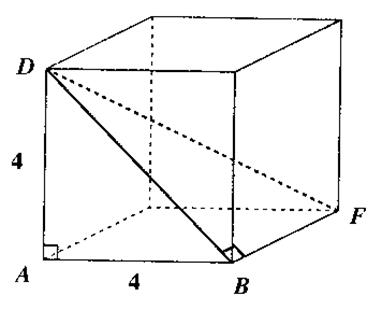
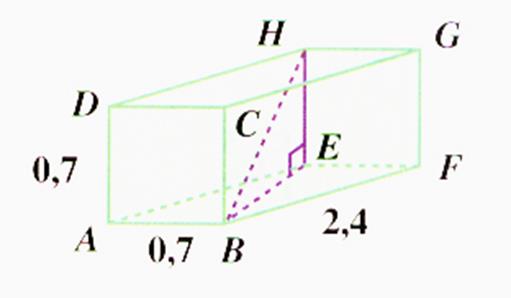
N° 2 : Calculer la diagonale du cube au dixième près.

Réponse :

DB » 5,7

DF » 6,9

3°) Autres séries d'exercices

Calculer la longueur « x »

4°)

Calculer la longueur « x »

5°)

Calculer la diagonale d’un cube de 1 m d’ arête .

6°)

Calculer la diagonale d’un parallélépipède rectangle ayant pour dimensions 7 ; 8 et 10 cm .

7°)

Calculer la diagonale d’un carré de 2,5 dm de côté

8°)

Calculer la longueur de AB

9°)

Calculer la longueur de la tangente AT (côtes en mm )

INTERDISCIPLINARITE :

Dans le bâtiment : pour effectuer un pavage dans une pièce .

Ce procédé permettant de tracer une droite perpendiculaire par exemple pour le pavage d’une pièce. ( les murs n’étant pas eux mêmes perpendiculaires ) On mesure AB = 6O cm sur la règle 1 , qui sert de base , puis on mesure AC = 80 cm sur la règle 2 , et on déplace la règle 2 de façon que BC mesure 1m. Les deux bords AB et AC forment un angle droit.

Remarques : Sur une surface plus réduite , on pourrait porter

AB = 6 cm AC = 8 cm ; il faut que BC mesure 10 cm .

Ou AB = 3 cm AC = 4 cm ; il faut que BC mesure 5 cm .

Ou AB = 12 cm AC = 16 cm ; il faut que BC mesure 20 cm .

Voir aussi la « corde à 13 nœuds ».

PROBLEMES DIVERS :

N°1 : Quelle longueur doit mesurer une échelle pour atteindre une fenêtre située à 6 m. Si on lui donne 1,5 mètres de pied ?

N° 2 : Calculer la diagonale du cube au dixième près. Réponse : DB » 5,7 DF » 6,9

N°3 Calculer la longueur de la diagonale du segment BH , au dixième près.

N°4 : Le cube à 5 cm d’arête. Calculer BA , AC et BC. Quelle est la nature du triangle BAC. ?

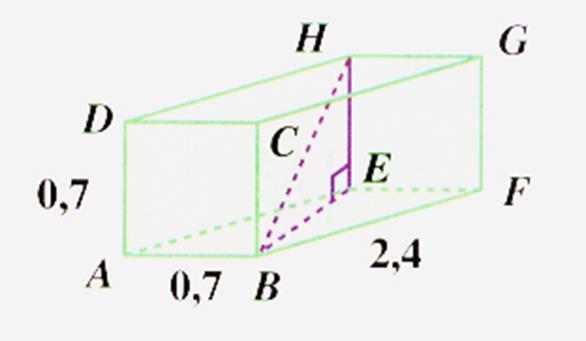
N°3 Calculer la longueur de la diagonale du segment BH , au dixième près.

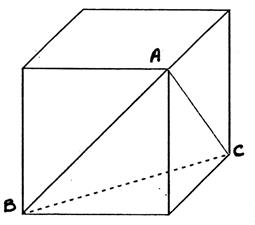
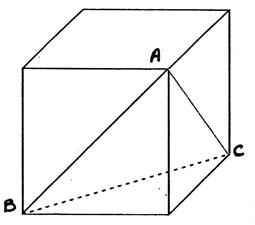
N°4 : Le cube à 5 cm d’arête. Calculer BA , AC et BC. Quelle est la nature du triangle BAC. ?