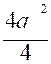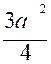|
|
|
TRAVAUX INTERDISCIPLINARITES :
PYTHAGORE.
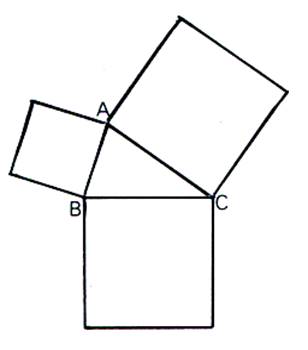
i Pour démontrer le théorème de Pythagore , Euclide
démontre que :
|
Si l’aire du carré ayant comme côté l ’
hypoténuse BC est égale à la somme de
l’aire du carré de côté AB et l’aire du carré de côté AC : on aura
démontré que BC2 =
AB2 + AC2 |
|
|
|
|
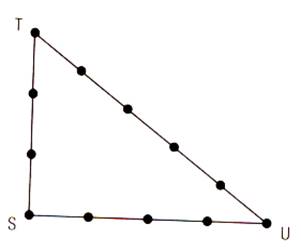
Pour tracer des angles droits , les Egyptiens
se servaient d’une corde fermée à 12 nœuds , régulièrement espacés ; ou
d’un segment de corde à treize nœuds
(régulièrement espacés) dont un nœud à chaque extrémité . Ils la tendaient entre trois
pieux de la façon ,
un en « T » ; un en « S » un en « U ». |
|
b ) diagonales
d’un quadrilatère et hauteur d’un
triangle .
|
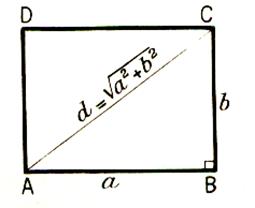
Diagonale d’un rectangle |
|
|
AC² = AB² + BC². Comme : DB² = DA² + AB² Si « d » = AC ; a =
AB ; b = CB Alors d ² = a² + b² Donc |
|
|
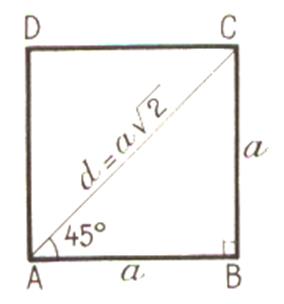
« diagonale du carré = a |
|
|
AC² = DB² = d ² Si AB = BC=CD=DA = « a » Alors d ² = a² + a² Soit d² = 2 a² Alors
Donc |
|
|
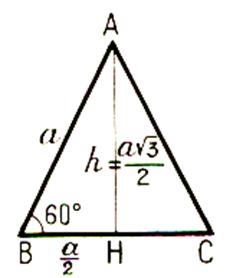
Hauteur du triangle équilatéral =
a |
||
|
a2
= ( a2
- ( a2
- h 2
= h 2
= |
|
|
|
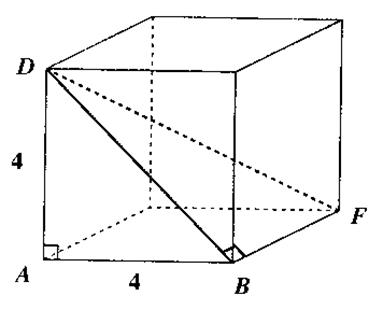
Voir dans
l’espace : on demande de calculer la diagonale d’un
cube , ou d’un parallélépipède rectangle . |
||
|
|
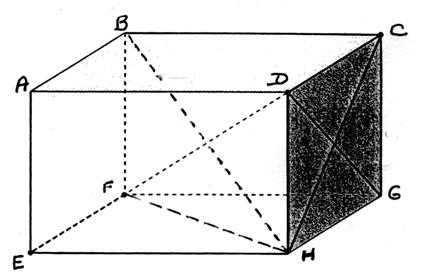
Exemples de demande
: -Calculer HC - Calculer FH - Calculer DF |
|
|
Triangle rectangle inscrit dans un demi - cercle . |
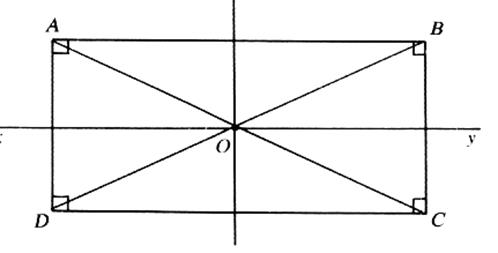
Rappel : le centre du cercle circonscrit dans un triangle
est se trouve au point d ’intersection des médiatrices des côtés du triangle .(
figure 2)
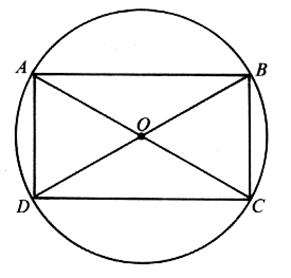
Observez
dans la figure ci - dessous : en traçant la diagonale AC du
rectangle ABCD , je divise le rectangle en deux triangle rectangle .Si
je trace la seconde diagonale DB , j’obtiens un point O situé à égal distance
des points , A ; B ; C ; D , je peux tracer un cercle passant
par ces 4 points .(figure 1 )
|
Figure 1 |
figure 2 |
|
|
|
l Soit "A" un point quelconque du demi - cercle de diamètre [ B C] .
Si un triangle ABC est
inscrit dans un demi - cercle de diamètre [ B
C] alors ce triangle est rectangle .
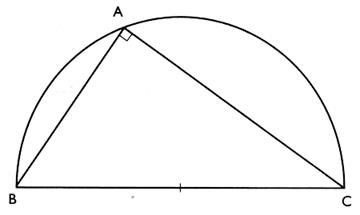
Activité :
Dessiner un demi - cercle de
diamètre BC = 8 cm .
Construire un triangle rectangle en A
dont le côté de l'angle droit mesure
3 cm .
Solution :
Pour que le triangle soit rectangle il suffit que le point A
appartiennent au cercle .L'hypoténuse
est le segment [ BC ] .
|
On retiendra : Pour identifier un triangle rectangle , on peut : -
vérifier que ses dimensions satisfont la réciproque de la propriété de Pythagore ; -
vérifier qu'il est inscrit dans un demi - cercle
dont le diamètre est l'hypoténuse du triangle . vérifier qu'un de ses angles
est droit à l'aide d'une équerre ou un
rapporteur. |
|
|
|
|
|
Autres séries
d'exercices |
|
|
3°)
|
Calculer la longueur « x » |
|
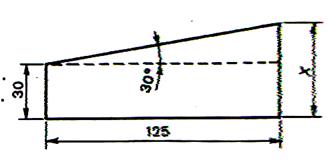
4°)
|
Calculer la longueur « x » |
|
5°)
|
Calculer la diagonale d’un cube de 1 m d’ arête
. |
|
6°)
|
Calculer la diagonale d’un parallélépipède rectangle ayant pour dimensions 7 ;
8 et 10 cm . |
|
7°)
|
Calculer la diagonale d’un carré de 2,5 dm de côté |
|
8°)
|
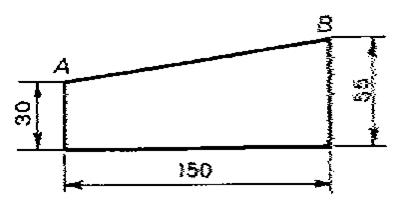
Calculer la longueur de AB |
|
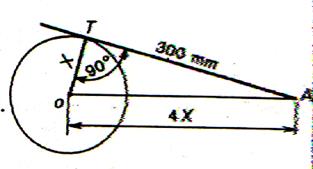
9°)
|
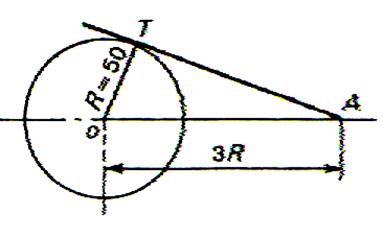
Calculer la longueur de la tangente AT (côtes en mm
) |
|
INTERDISCIPLINARITE :
Dans le bâtiment : pour effectuer
un pavage dans une pièce .
|
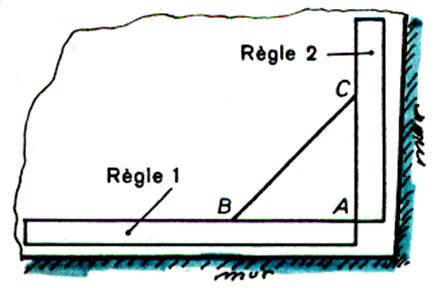
Ce procédé permettant de tracer une droite
perpendiculaire par exemple pour le pavage d’une pièce. ( les murs n’étant pas eux mêmes perpendiculaires ) On mesure AB = 6O cm sur la règle 1 ,
qui sert de base , puis on mesure AC = 80 cm sur la règle 2 , et on déplace
la règle 2 de façon que BC mesure 1m. Les deux bords AB et AC forment un angle droit. |
|
Remarques : Sur une surface plus réduite
, on pourrait porter
AB = 6 cm AC = 8
cm ; il faut que BC mesure 10 cm .
Ou AB = 3 cm AC = 4 cm ; il faut que BC mesure 5 cm .
Ou AB = 12 cm AC = 16 cm ; il faut que BC mesure 20 cm .
Voir aussi la « corde à 13
nœuds ».
PROBLEMES DIVERS :
|
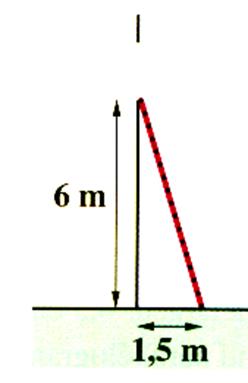
N°1 : Quelle longueur doit mesurer une échelle pour atteindre une
fenêtre située à 6 m. Si on lui donne 1,5 mètres de pied ? |
|
|
N° 2 : Calculer la diagonale du cube au dixième près. Réponse : DB » 5,7 DF »
6,9 |
|
|
N°3 Calculer la longueur de la
diagonale du segment BH , au dixième près. |
|
|
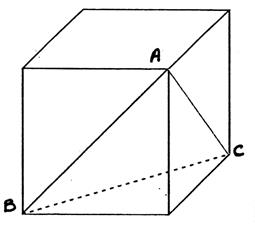
N°4 : Le cube à 5 cm d’arête. Calculer BA , AC et BC. Quelle est la nature du triangle BAC. ? |
|