Classe de 4^ème collège

>>>>>>>Vers le corrigé >>>>>>>

Voir programme 4^ème

La perpendiculaire (primaire)

Nomenclature 1

Droite

Index : warmaths .

Objectif précédent   :

1. Verticale et horizontale
2. Rappel : les droites perpendiculaires vu en 6^ème collège.
3. Cours sur les perpendiculaires .

Objectif suivant :

Tracés d’une perpendiculaire.

2°)Géométrie dans l’espace :l’orthogonalité

Tableau      

Liste des cours sur les « angles »

Fiche de travail sur :

Définition .

Directions orthogonales.

TEST

COURS

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité

Perpendicularité et plan

Corrigé Contrôle 

Corrigé évaluation 

Définition :

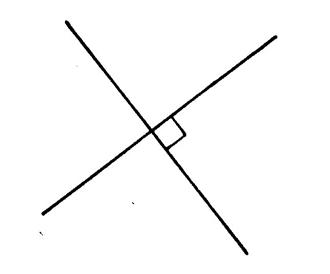
On appelle « droites perpendiculaires » deux droites qui déterminent entre elles quatre angles ……… …

Remarque :

Par abus de langage , on dit aussi « segments perpendiculaires », mais cela signifie « segments dont les supports sont perpendiculaires ».

Nous allons récapituler ici les propriétés étudiées en 6^ème et 5^ème ….

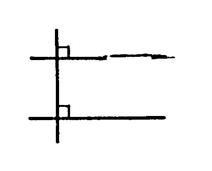
Propriété 18 :

Etant donné un point et une droite, il existe une droite et une seule passant par le point et  perpendiculaire à la droite.

Propriété 19 :

Si deux droites sont perpendiculaires  à une droite  alors elles sont  ……………………… .

Propriété 20 :

Si deux droites sont parallèles , toute perpendiculaire à l’une est alors ……………………….  à l’autre.

Directions orthogonales.

Info +++@

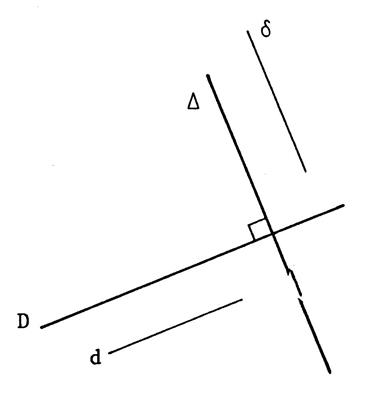
Lorsque deux droites sont parallèles , on dit qu’elles ont même direction .

Considérons une droite « D » de direction « d »  et une droite «  »  de direction «  ».

Dans le cas où « D » est perpendiculaire à  «  »  , toutes les droites perpendiculaires à «  »  sont  ……………………………….  à « D »  ( propriété n° ……. ) .

Elles ont donc la direction «…… ».

Inversement , toutes les droites de direction « d » sont parallèles à « …………. » , elles sont donc …………………………………… à  «  »  . (propriété n° ………………..) .

De même , l’ensemble des droites perpendiculaires  à «D » est l’ensemble des droites de direction  «  ».

Dans ces conditions , on dit que les directions « d »  et  «  » sont orthogonales.

Activité :

« ABC » est un triangle rectangle en « A » .

« M » est le milieu de [ AC] . « D » est le symétrique de « B » par rapport à « M ».

Démontre que (CD) est perpendiculaire à ( AC ) .

Fait le 22 /9/ 2014