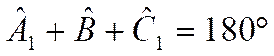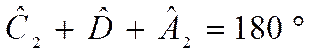|
Niveau V. |
Géométrie : DOSSIER :
les tracés géométriques II / Objectif cours
24b |
|
|
|
|
|
|
|
|
|
|
|
|
ENVIRONNEMENT du dossier:
|
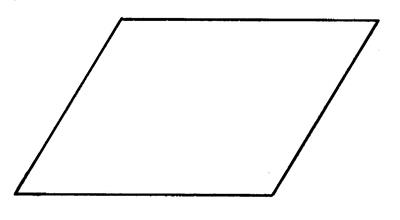
Voir le parallélogramme |
|||
|
|
|
|
|
DOSSIER : LES QUADRILATERES
|
1.
« Définition
et présentation des figures »(A,B,C,D) ; |
|
|
|
|
2.
Définitions :
Concaves et convexes et croisés. ( et Somme des angles ……..) |
|
|
|
3.
Les irréguliers |
|
|
|
4.
A deux côtés
parallèles |
|
|
|
5.
A côtés
parallèles deux à deux. |
|
|
TEST |
COURS |
Devoir évaluation |
|
|
|
COURS
|
|
I ) Les quadrilatères
Définition: un quadrilatère est une figure géométrique qui possède 4 cotés.
|
Rappel 1: « Domaine plan » ou « surface
plane ». On
appelle « domaine plan » ou « surface plane » toute portion de plan. · Le quadrilatère est une portion de plan. |
|
Rappel 2 : « convexité » d’un
domaine plan. On dit qu’un domaine plan est convexe si le
segment joignant deux points quelconques du domaine est entièrement dans le
domaine. « concavité » :
on dit qu’un domaine plan est concave si le segment joignant deux points
quelconques du domaine n’est pas entièrement dans le domaine. |
On dit
aussi qu' : Un quadrilatère
est un polygone qui a quatre cotés. Il existe deux
sortes de quadrilatères:
|
|
|
|||
|
|
|
|||
|
Les quadrilatères
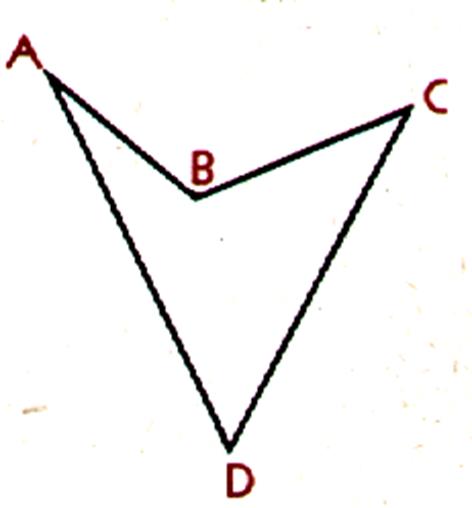
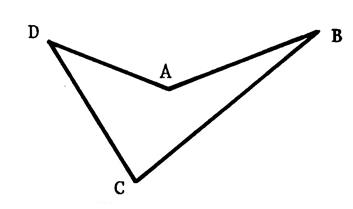
« concaves » ( non convexes) |
||||
|
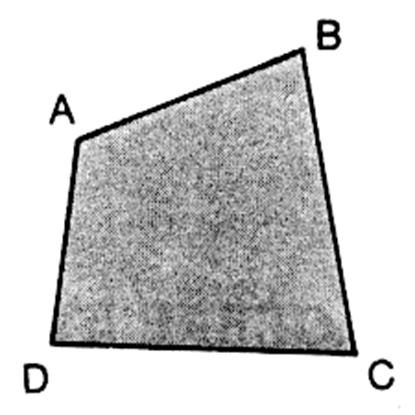
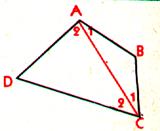
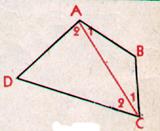
Le premier point cité est le point le plus en haut à gauche
ici « A »
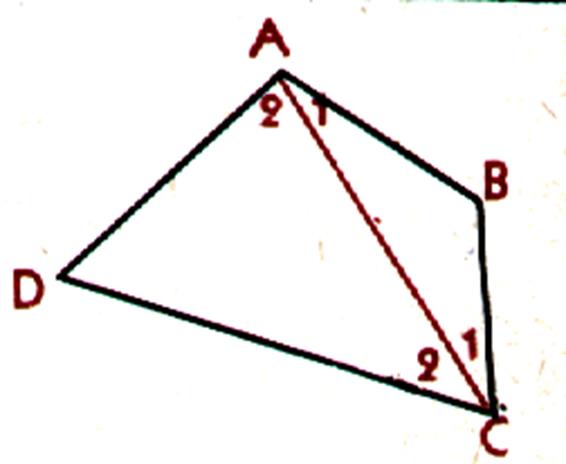
La diagonale AC détermine deux triangles ABC et ADC
, on sait que:
En additionnant ces deux égalités:
|
Le quadrilatère est concave : Le segment AC n’est pas tous ses
points dans le quadrilatère !!!
|
|||
|
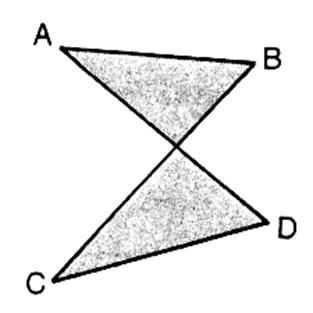
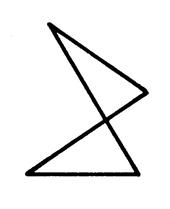
Exemple de
quadrilatère « croisé »
|
||||
|
II ) Les
quadrilatères "irréguliers": Exemples:
|
||||
|
Exercices:
nommez tous les quadrilatères que vous pouvez recenser |
||||
|
|
Somme des angles d’un quadrilatère non – croisé. |
|
|||
|
|
|
|
|||
|
|
Concave. |
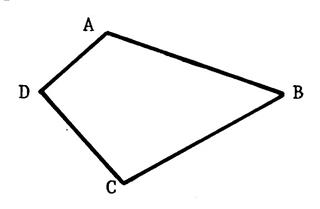
Convexe |
Croisé |
|
|
|
|
|
|
|||
|
|
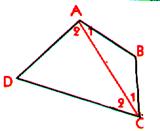
Ci-dessus vous avez deux
quadrilatères : l’un concave et l’autre convexe. Ils sont non - croisés. Activité : Tracez la diagonale [AC] . Vous déterminez ainsi deux
triangles : « CDA » et « ABC ». Conclusion : La somme des angles du
quadrilatère est égale à la somme des angles des 2 triangles. |
|
|
||
|
|
|
|
|||
|
|
A retenir : La somme des angles d’un quadrilatère non-croisé
est égale à …..360°…… |
|
|||
III)
QUADRILATERES ayant deux cotés parallèles
LES TRAPEZES
|
« ils
ont deux côtés parallèles » |
|
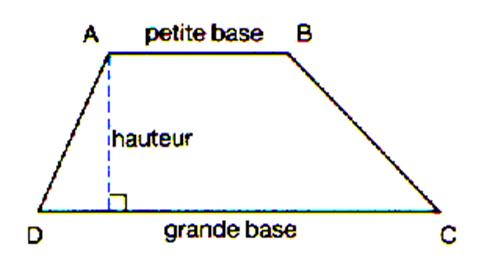
Le
trapèze quelconque
Info +++
Ll’axe se symétrie des deux parallèles passe par les
milieux des côtés AD et BC et les diagonales AC et BD. |
|
|
|
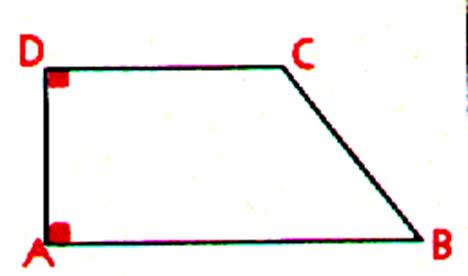
Le
trapèze rectangle Un côté est
perpendiculaire aux côtés parallèles. |
|
|
|
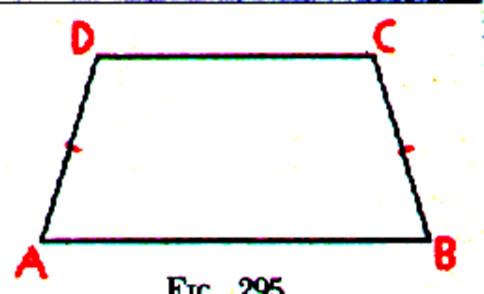
Le
trapèze isocèle Il
possède un axe de symétrie. |
|
|
IV )
QUADRILATERES ayant deux cotés parallèles deux à deux
NOM :
|
INFO + |
|
Le
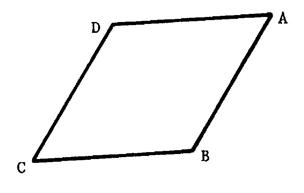
parallélogramme
Quadrilatère convexe dont les côtés opposés sont parallèles deux à deux . [DA ] // [ BC ] et [ AB] // [ CD ] |
|
|
|
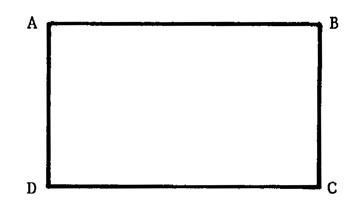
Définition : Parallélogramme
ayant un angle droit . ( 1)
AB >
BC alors [ BC ] est la largeur et [ AB] est la
longueur |
|
|
|
Définition : |
|
Définitions : Rectangle
ayant deux côtés consécutifs isométriques Ou Losange
ayant un angle droit AB = BC =
CD= DB = a
|
CONTROLE :
1.
Donnez la
définition d'un quadrilatère
2.
Donner le
nom de 5 quadrilatères « particuliers »
Série 1 :
1) Tracer un
quadrilatère convexe.
2 ) Tracer un quadrilatère non convexe.
3°) Construire
à la règle et au compas la médiatrice ( D) d'un segment AB de
Placer sur la médiatrice deux points C et D situés de part et d'autre de F tels que F
soit le milieu de [ C D ] . Que
représente la droite ( AB) pour le segment [ CD] . Quelle est la nature du quadrilatère
ACBD ?
Série 2 :
EXERCICES DE CONSTRUCTION : Tracer les figures suivantes ………
Interdisciplinarité :
en ébénisterie.
Formule calcul du nombre de queue d’aronde à répartir sur la
largeur d’une planche . La queue d’aronde est un trapèze .
![]()
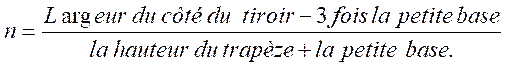 ou
ou 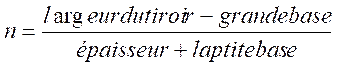
la petite base =
épaisseur divisée par 5
Les
parallélogrammes
|
1°) Parallélogramme ABCD de côtés AB = |
|
|
2°)
Parallélogramme ABCD tel que AB = |
|
|
3°)
Parallélogramme ABCD de côté AB = 5cm
et de diagonales AC = |
|
|
4°)
Parallélogramme ABCD tel que AB =
2,5cm et AD = 5cm et la diagonale AC = |
|
|
5°)
Parallélogramme ABCD de côtés AB = 5cm et AD = 4cm et de hauteur AH = 3cm |
|
|
6°)
Parallélogramme ABCD de côté AB= |
|
|
1°) Rectangle ABCD tel que AB = 55mm et AD = |
|
|
2°) Rectangle ABCD de diagonale |
|
|
3°) En +++ : Rectangle ABCD de diagonale |
|
|
4°) En plus : rectangle ABCD de longueur
triple de la largeur et de périmètre |
|
|
1°)Losange ABCD tel que
AB = |
|
|
2°) Losange ABCD de diagonales AC = |
|
|
3°) Losange
ABCD de diagonale BD = |
|
|
4°) En
plus : losange d’aire A = 6cm2 et de diagonale AC = |
|
|
1°) Carré de côté AB = |
|
|
2°) Carré de diagonale AC = |
|
|
4°) En plus : carré de périmètre p = |
|
|
5°)En plus : carré d’aire A = 1225 mm2 |
|
|
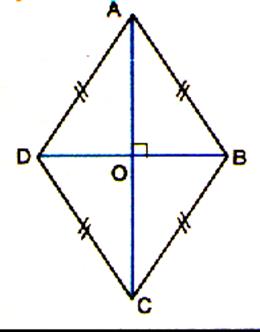
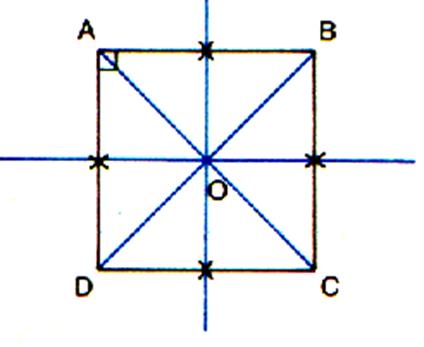
Exercices
d’identification : Soit le
parallélogramme ABCD et « O » le point d’intersection des
diagonales |
|
Consignes : mettre une croix pour les figures
concernées ; justifier.
|
Propriétés ou caractères |
trapèze |
Trapèze
isocèle |
Trapèze
rectangle |
parallélogramme |
rectangle |
Losange
|
Carré
|
justification |
AB // DC
|
|
|
|
|
|
|
|
|
|
AO =OC= OD = OB |
|
|
|
|
|
|
|
|
|
AB = BC=CD=DA |
|
|
|
|
|
|
|
|
|
AB//DC et |
|
|
|
|
|
|
|
|
|
BC // AD et |
|
|
|
|
|
|
|
|
|
AB = CD et AD = BC |
|
|
|
|
|
|
|
|
|
Rectangle et AB = BC |
|
|
|
|
|
|
|
|
|
Parallélogramme tel que AC ^ BD |
|
|
|
|
|
|
|
|
|
Propriétés ou caractères
|
trapèze |
Trapèze isocèle |
Trapèze rectangle |
parallélogramme |
rectangle |
Losange |
Carré |
justification |
|
AD // BC et |
|
|
|
|
|
|
|
|
|
AB //CD Et AD // BC |
|
|
|
|
|
|
|
|
|
Losange tel que |
|
|
|
|
|
|
|
|
|
AB //DC et AB =DC=BC |
|
|
|
|
|
|
|
|
|
Médiatrice de AB et médiatrice de DC confondues |
|
|
|
|
|
|
|
|
|
AB // CD et AB = CD |
|
|
|
|
|
|
|
|
|
[AC] et [BD ] médiatrices l’une de l’autre |
|
|
|
|
|
|
|
|
|
AD // BC et AB = CD |
|
|
|
|
|
|
|
|
|
m(A,C) = m
( B,D)= 0 |
|
|
|
|
|
|
|
|
|
Propriétés ou caractères
|
trapèze |
Trapèze
isocèle |
Trapèze
rectangle |
parallélogramme |
rectangle |
Losange
|
Carré
|
justification |
|
Losange tel que AC = BD |
|
|
|
|
|
|
|
|
|
m(A,C) et m (B,D) =
0 et AC = BD |
|
|
|
|
|
|
|
|