La symétrie centrale : corrigé du CONTROLE

1°) Qu’appelle-t-on : symétrie centrale ?

Définition : Soit un point M et un point O donné , on appelle symétrie centrale de centre O l’application du plan P dans le plan P qui associe à tout point ( M ) le point ( M’) tel que O soit le milieu du segment MM’ .

2°) traduire la notation suivante :

Notation :

S_o : P ® P

M a M’ | O = milieu [MM’]

Il y a symétrie centrale de centre O l’application du plan P dans le plan P qui associe à tout point ( M ) le point ( M’) tel que O soit le milieu du segment MM’ .

3°) Que conserve une symétrie centrale conserve l’alignement ; les longueurs et les angles ? .

Une symétrie centrale conservant l’alignement ; les longueurs et les angles , il en résulte que toute figure ( cercle ; triangle , quadrilatère ) à pour image une figure du même type et de mêmes dimensions , donc de même aire .Une symétrie centrale conserve les aires

4°)quelles sont les figures qui admettent un centre de symétrie ?

le parallélogramme ; le rectangle ; le carré ; le losange et le cercle .

5°)Compléter la phrase suivante : ( 5^e)

le parallélogramme ; le rectangle ; le carré ; le losange admettent un centre de symétrie qui est le point ……d’intersection des diagonales…………….. 

6°)le cercle admet un pour centre de symétrie ……son centre……………..

EVALUATION

Exercice N°1
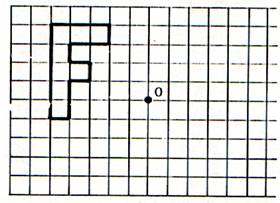
En utilisant le quadrillage , dessiner l’image de la lettre « F » dans la symétrie centrale de centre O.

Exercice N°2
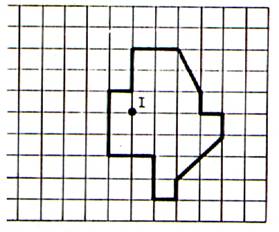
En utilisant le quadrillage , dessiner l’image de la figure ci contre et reproduire son image dans la symétrie centrale de centre I.

Exercice N°3
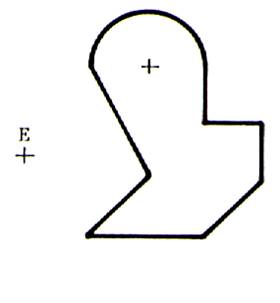
Dessiner avec la règle et le compas la symétrie de la figure ci-contre de centre E

Exercice N°4
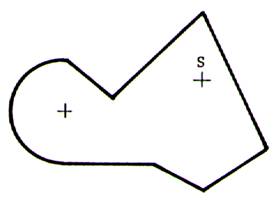
Dessiner avec la règle et le compas la symétrie de la figure ci-contre de centre S