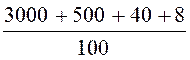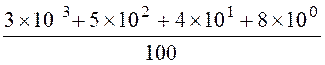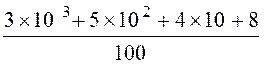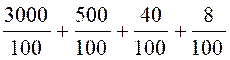|
Aller vers lire….la numération , ne pas
confondre : « nombre » et « grandeur » |
Pré requis:
|
|
|
|
Nomenclature |
|
|
Division de N par
10 ; 100 ;1000 |
ENVIRONNEMENT du dossier:
|
Objectif
précédent : |
1°) Numération des nombres décimaux. |
||
|
|
|
|
|
37 DOSSIER: LE NOMBRE DECIMAL
1. Définition.
2. Tableau de numération et écriture.
3. Décomposition d’un nombre décimal en
« somme »
|
COURS |
Interdisciplinarité Devoirs |
|
|||||
|
|
|
|
|
>>>
Liste de fiches de travaux |
|
|
|
Tous
les nombres décimaux sont regroupés dans un même ensemble de nombres .
L’ ensemble
des nombres décimaux se note par la lettre : D
voir NUMERATION et Division des « N » par 10 ;100 ;
1000 et le système décimal
|
|
Rappels N°1:définitions. NOMBRE : un nombre est un alignement horizontal de
chiffres. Le nombre sert à mesurer des « quantités ».
. GRANDEUR : on appelle « grandeur » un nombre associé à une unité. ARITHMETIQUE : Une
fraction est une ou plusieurs
parties égales de l’unité . Exemple : un décimètre de tissu ,
les deux cinquièmes d’une pomme , .. ; Une fraction est dite décimale quand l’unité est
partagée en 10 ; 100 ;
1000 ; … parties égales .
Une unité vaut 10 dixièmes , 100 centièmes , ou 1 000 millièmes , etc. … Les dixièmes , centièmes , ou millièmes ,etc. sont des parties de l’unité de 10 en 10
fois plus petites les unes que les autres . Un nombre décimal est un nombre entier accompagné
d’une fraction décimale . Exemple : Pour écrire un nombre décimal ,
on écrit d’abord la partie entière , puis la fraction décimale , et l’on a
soin de séparer l’une de l’autre par une virgule. Exemple : 24 unités 35 centièmes s’ écrivent 24,35 . Quand le nombre ne comprend pas d’unités , on remplace la partie entière par un zéro . * Exemple : 246 millièmes s’ écrivent 0,
246 |
|
Ci-dessous :
Tableau classant les parties décimales d’un nombre « décimal »
|
Partie entière du nombre décimal. |
virgule |
Partie décimale
du nombre décimal. |
|||||||||||||||||
|
dizaine |
|
unité |
|
dixièmes |
|
centièmes |
|
millièmes |
|
dix millièmes |
|
Cent millièmes |
|
millionièmes |
|
|
|
|
|
|
|
|
0 |
, |
2 |
|
4 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
6 |
, |
2 |
|
6 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ecritures numériques : |
|
le premier chiffre après la virgule s’appelle : le « dixième » (
qui représente une partie d’une unité divisée en dix parties égales) |
0,1 ;
1/10 ; 1 |
|
le deuxième chiffre après la virgule qui représente une partie d’une unité
divisée en « centièmes » d
‘ unité ( voir
les dixièmes de dixième ) |
0,01 ; 1 /100 ; 1 |
|
le
troisième chiffre après la
virgule qui représente une partie d’une unité divisée en « millièmes » d’unité |
0,001 ; 1 / 1000 ; 1 |
; et ainsi de suite ( le dix millième ; ……….)
|
|
On retrouve regroupés et classés ces chiffres dans le tableau
suivant : Dans le cas
de plus grand nombre des colonnes peuvent compléter ce tableau , du coté des multiples comme
du côté des s sous multiples II ) Le tableau de
numération : Ce tableau , doit être connu de tous , il permet de lire facilement un
nombre DECIMAL : |
|
|
Partie entière (multiples ) |
Partie décimale (sous multiples) |
||||||||||||||||||
|
Ici :la colonne des « dixième » |
Ici : le « centième » |
||||||||||||||||||
|
cent aines |
dizaines |
unités |
cent aines |
dizaines |
unités |
cent aines |
dizaines |
unités |
0,1 |
ou |
1 /10 |
0,01 |
ou |
1/100 |
0,001 |
ou |
1/1000 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Remarque
importante : ne pas oublier qu’une virgule sépare les chiffres de la
partie entière et les chiffres de la partie décimale. Pour
comprendre l’existence de cette virgule on doit se souvenir qu’un nombre à
virgule est l’écriture simplifiée d’une addition : Exemple :
1,16 est en fait la somme de deux nombres : le nombre « 1 » plus
le nombre « 0,16 »
: tel que « 1 + 0,16 » ‘s’écrit
par convention : 1,16 Ce qui
fait dire que tout nombre décimal se décompose en deux parties distinctes. (
la partie entière et la partie décimale). Décomposition d’un nombre décimal en
« somme » : Exemple
a = 35 ,
48 unités a = 3 soit a = 3 que l’on peut écrire aussi : a
= 3 soit l’addition : a = 30
unités + 5 unités + a = 30
unités + 5 unités + 0,4
unités + 0,08
unités De façon simplifiée , nous obtenons bien : 30 + 5 + 0,4 + 0,08 = 35
, 48 On peut
aussi écrire que : Un nombre décimal peut être représenté par une fraction décimale ; il
peut s’écrire sous forme de nombre rationnel ; Exemple : a = 35 ,
48 =
qui
devient : a = 3 a = 30 +
5 + 4 Le nombre décimal peut être représenté sous forme d’une décomposition
de termes de 10 n. (
avec « n » positif ou négatif) Avec « la convention de
la virgule » entre le chiffre des unités et le terme en 10-1 , on obtient l’écriture commode : a =
35 , 48 Lecture
et décomposition du nombre
3542,68 : C’est
un nombre décimal : Sa partie entière est « 3542 » ( partie à gauche de la virgule) Sa partie décimale est « 0,68 » (
partie à droite de la virgule) Si la partie décimale ne comporte que des zéros ,
le nombre entier : 34 = 34 , 0 = 34,00 … pour pouvoir comparer des
nombres , ou faire des opérations , il faut savoir ce que représente la position
de chaque chiffre. Pour cela on utilise un tableau : . 3542,68 = 3 I ) Lire à haute voix : 843 546791,4 71 043,051
4230040,25 500 008003,08 II ) 1 ) Citer
dix nombres compris entre ....0...........et ....1.............. ; par
ordre croissant. 2 ) Citer dix nombres compris entre ......1,
1.........et ....1,2.......... ; par ordre croissant. 3 ) Citer dix nombres compris entre
......1,21.........et ..1,22........... ; par ordre croissant. 4 ) Citer dix nombres compris entre
....47,31...........et ..47,32................ ; par ordre croissant. ) Citer dix nombres compris entre
...504............et ..504,1................ ; par ordre croissant. |
|
TRAVAUX AUTO FORMATIFS (devoir formatif)
1 ) Qu ‘est qu ’ un nombre ?
2 ) Qu’est ce qu’une
grandeur ?
3 ) A quoi sert le nombre ?
4 ) Qu ‘est ce
qu’un nombre décimal , en combien de parties se
compose-t-il ?
5
)Représenter le tableau permettant de nommer un nombre décimal.
EVALUATION
I
) Lire
à haute voix : 843
546791,4 71 043,051 4230040,25 500
008003,08
II )
1 ) Citer dix nombres compris
entre ....0...........et ....1.............. ; par ordre croissant.
2 ) Citer dix nombres compris entre ......1, 1.........et
....1,2.......... ; par ordre croissant.
3 ) Citer dix nombres compris entre ......1,21.........et ..1,22........... ;
par ordre croissant.
4 ) Citer dix nombres compris entre ....47,31...........et
..47,32................ ; par ordre croissant.
) Citer dix nombres compris entre ...504............et
..504,1................ ; par ordre croissant.