Pré requis:
|
Fonctions
pré requis |
||
|
Les fonctions informations |
||
|
Pré requis (calculs) |
|
Cours fin de troisième –BEP –
Seconde. |
ENVIRONNEMENT du dossier:
|
Retour
vers accueil « warmaths » |
Objectif précédent : |
Objectif suivant : |
DOSSIER : NOMENCLATURE :
« FONCTION » et « APPLICATION »…
|
TEST |
COURS |
Devoir évaluation |
Interdisciplinarité |
|
|
Préambule : |
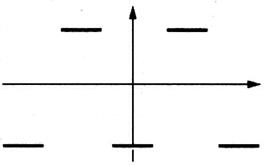
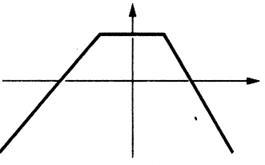
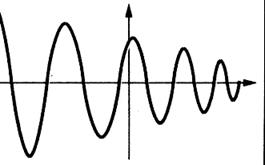
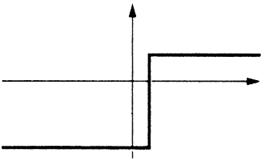
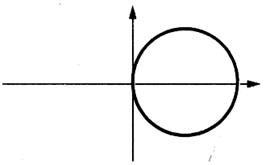
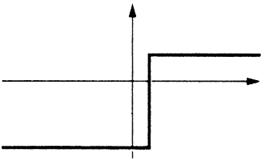
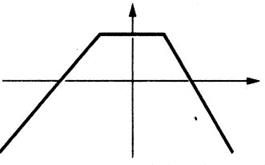
Exemples d’une Représentation graphique d’une
fonction ou d’une fonction.(voir la définition ci dessous) |
|
Exemples de tracés représentant une fonction :
|
|
|
|
|
A
une valeur de « x » correspond au plus une valeur de
« y » |
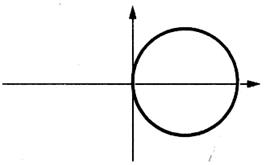
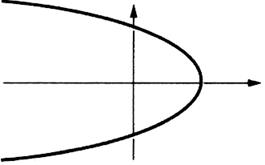
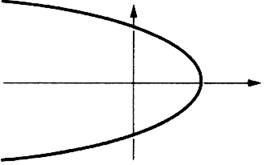
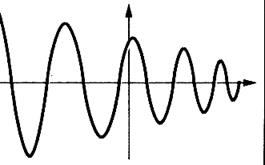
Exemples de tracés ne représentant pas une
fonction :
Remarquez qu’ à une valeur de « x »
correspond plus d’une valeur de « y »
|
|
|
|
|
A
une valeur de « x » correspond plus d’une valeur de « y » |
Généralités : vocabulaire
Préalable : recherchez dans le dictionnaire
les définitions du mot
« fonction » et « application »
|
Les ensembles de nombres;
sont désignés par les
lettres : N ;
D ;Q ; D+ ;
D- ; R ( pour les plus utilisés) |
|
l
la lettre « f » est
utilisée pour désigner le mot «
fonction » .
l
Pour définir une « fonction »
il nous faudra deux ensembles de nombres; qui sont un
« ensemble de départ » et
un « ensemble d’arrivé » :
Le premier ensemble de
nombres que l’on prend s’appellera « ensemble de départ »
Les nombres (ou éléments) qu’il contient vont servir à « construire » un second
ensemble de nombres qui lui s’appellera « ensemble
d’arrivée » .
-
Ensemble de départ :
ò Désignation : Un ensemble
(dit) de départ désigné est par une lettre majuscule ; par
commodité nous choisirons de le nommer par la lettre « E » dans
lequel chaque élément de l’ensemble sera représenté par une lettre minuscule
affecté d’un indice ( nous choisirons
la lettre « x ») .
ò Représentation de l’écriture
mathématique de l’ensemble de départ :
E = í x1 ; x2 ; x3 ;
......xn ý ou E = í x1 ;
x2 ; x3 ý
-
Ensemble d’arrivé :
ò Un ensemble (dit) d ’ arrivée
est désigné est par une lettre
majuscule ; par commodité nous choisirons la lettre « A » dans lequel chaque élément de l’ensemble sera
représenté par une lettre minuscule affecté d’un indice ( nous choisirons la lettre « y ») .
ò représentation de l’écriture
mathématique de l’ensemble d ’
Arrivée :
A = í y1 ; y2 ;
y3 ; ......yn ý
ou A = í y1 ;
y2 ; y3 ý
l
Information sur l’expression « EN
FONCTION » en
« f »
en fonction peut signifier « faire
avec » ...quelque chose choisie ou imposée.
On peut faire en
fonction ...du temps
On peut faire en
fonction ...de l’outil disponible
On peut faire en
fonction .....des moyens dont on dispose.
òEn mathématique on trouve une valeur à « y » en fonction d’une valeur de « x »
(choisie ou imposée) : au lieu d’écrire la phrase « y » en fonction d’une valeur de « x » , on la remplace par (tout simplement) : y =
f(x) )
« La valeur de l élément de
l’ensemble d’arrivée » ( y ) est
obtenue par le calcul et en fonction de la valeur
« donnée ou choisie » de
« x » .
On
dit alors : qu’ «
il y a une
« relation entre y
et x » et on
le traduit
Traduction
mathématique : y R x (on utilise la lettre R pour remplacer
le mot « relation »)
«On dit
aussi : pour qu’il y ait une fonction il faut qu’il existe une relation
mathématique entre les éléments
de l’ensemble de départ et les éléments de l’ensemble d’arrivé »
Puisque
« y 1 » est obtenu en fonction de « x1 » ;
que « y2 » est obtenu en fonction de « x2 » ;
.......on peut remplacer « y1 »
par « f(x1) » ; « y2 » par
« f(x2) » ;
…….. ainsi de suite .
On peut
donc écrire et remplacer :
|
A = í y1 ; y2 ;
y3 ; ......yn ý |
par |
A= í f(x1) ;f(x2) ;
f(x3) ; ......f(xn) ý |
|
Ou |
|
|
|
A = í y1 ; y2 ;
y3 ý |
par |
A = í f(x1) ;f(x2) ;
f(x3) ý |
lExemple d’une situation de la vie courante
où l’on utilise les ensembles (de départ et d’arrivée) :
Un automobiliste a observé
sa consommation de carburant à différentes vitesses .Il a obtenu le tableau
suivant :
|
vitesse en Km/h |
50 |
60 |
70 |
80 |
90 |
100 |
110 |
|
Consommation en L |
5,4 |
6,2 |
6,9 |
7,8 |
8,7 |
9,3 |
10,1 |
L’ensemble de
départ est « vitesse », que l’on choisira de noter « V »,
elle est mesurée et donnée par un nombre (élément de l’ensemble de départ)
donc V = í
50 ;60 ;70 ;80 ;90 ;100 ;110 ý
L’ensemble
d’arrivée est « consommation » , noté « C » ;elle est
mesurée et donnée par un nombre (élément
de l’ensemble d’arrivée) :
donc
C =í 5,4 ; 6,2 ; 6,9 ;
7,8 ; 8,7 ;9,3 ; 10, 1 ý
òAnalyse du tableau :
òOn remarque : qu’il y a autant d’éléments dans
l’ensemble « V » que dans l’ensemble « C »
que chaque élément
de « V » à « pour
image » un élément de « C »
(par
exemple : 70 à pour image 6,9)
Convention :
On
remplacera l’expression « a pour image » par le
dessin : 
(
flèche orientée de vers la droite, la flèche aura un talon (trait
vertical lié) )
Ainsi dans l’exemple , on remplacera l’écriture « 70 a pour image 6,9 »
par l’écriture 706,9
En
généralisant :Si v1 est un élément de « V »
et c1 l’élément correspondant
« C » ,on dira que :
« v1 a pour image c1» ;
on traduira en écriture mathématique :
v1c1
il y a
fonction de « V » vers « C »
On remarque qu’à chaque élément de
« V » correspond un élément unique
de « C », on dira que l’on a
une fonction de l’ensemble « V » vers l’ensemble
« C ».
Par convention : on
remplacera le mot vers par le
symbole : 
;
(c’est une flèche simple(sans talon) orienté vers la droite )
On
remplacera l’expression : il y a
fonction ( f ) de « V »
vers « C » par
L’écriture : f : V C
Qu’il faudra traduire par : il y a fonction de
l’ensemble de départ « V »
vers l’ensemble d’arrivée « C »
.
« Fonction »
lGénéralisation :
On
dira qu’il y a « fonction » de
l’ensemble de départ ( E) vers l’ensemble
d’arrivée ( A),si à chaque élément de l’ensemble de départ correspond un
élément unique ( 0 ou 1 image ) de l’ensemble d’arrivée.
Notation
(traduction en écriture symbolique ) f : E
A
Traduction
en écriture littérale : de
f : E A
« f :
» Lire : il y a fonction
« E
» Lire : de
l’ensemble de départ nommé
« E »
« » Lire : la
flèche signifie « vers »
« A
» Lire
: L’ensemble d’arrivé .nommé
« A »
nota concernant les
ensembles (les plus usités) :
Les ensembles sont des ensembles de
nombres : N ;
D ; D± ; R ;….
ò On précisera : Si « x1 » est un élément
de « E » (ensemble de départ) et
« y1 » l’élément de « A » (ensemble d’arrivée),
on dit que : « x1 » a pour image
« y1 ».
nota : On dira aussi que « y » est
l’image de « x » par f.
Exemple : on écrit
f ( 3) = 6 : on dit que :
« 6 » est l’image de « 3 » par f….
le groupe de mots : « x » a pour image
« y » se notera : x y (info : On remplace
le « a pour image » par une « flèche à talon ») :
Notation complémentaire ( traduction en écriture mathématique ) x
y
On désigne
« la fonction » par
la lettre
« f », , l’image
de « x » (cette image « y » est obtenue en fonction de la valeur de « x ») se note alors f(x) (
lire : éff de ixe)
Ainsi l’écriture :
x y
peut s ’écrire ,aussi, x f(x) ; Ces deux écritures mathématiques sont
équivalentes.
Nota : « antécédent » : on peut aussi dire que « y » est
l’antécédent de « x » par f
(x)
Exemple : si on écrit
f ( 3) = 6 : on dit que l’antécédent de « 6 » par f
est « 3 ».
Plus
précisément un exemple d’application ::
soit la table de multiplication des
« 2 » ; je dis que cette
table correspond la fonction ( que je reconnais comme
étant la forme de la fonction dite : linéaire): f(x)
= 2x
j’écris aussi que x x 
y et
appliqué au cas : x 2x
( je dis que « x » (dans l’ensemble des nombres de départ) à pour image « 2x » (dans l’ensemble des nombres d’arrivés ; valeurs
obtenues par le calcul « fois
2 » ) )
en résumé :
|
Soit la fonction |
f(x)
= 2x |
|
|
|
|
|
|
|
x |
Exemple 1 : Ce qui
signifie que pour « x=3 » je fais le calcul 2 fois 3 ;
j’obtiens « 6 » |
|
|
||
|
|
|
Exemple 2 : Ce qui
signifie que pour « x = 7 » je fais le calcul 2 fois 3 ;
j’obtiens « 14 » Et ainsi de suite ….. |
|
|
||
|
|
|
|
|
|
|
|
|
Si x = 3 |
Alors 3 |
Soit |
3 |
« 6 » |
|
|
|
|
|
« 3 » est l’élément de départ . |
|
« 6 » est l’élément dans l’ensemble
d’arrivé |
|
|
|
|
|
|
|
Et |
|
|
|
|
|
|
Pour obtenir « 6 » j’ai fais le calcul « 2 » fois
« 3 » Alors je peux dire que « 3 » est
l’antécédent de « 6 » dans la fonction : f(x) = 2x |
|||
|
|
|
|
Pour obtenir « 14 » j’ai fais le calcul « 2 » fois
« 7 » Alors je peux dire que « 7 » est
l’antécédent de « 14 » dans la fonction : f(x) = 2x |
|||
ò
Pour étudier une fonction on nous donne souvent une relation (désignée par la lettre :R. ) mathématique
qui nous permet de calculer une valeur
« y » en fonction de la valeur
de « x » (choisie ou imposée)
exemples :
·
la relation qui lie « x » à
« y » est 2x ; on peut
alors écrire f ( x ) = 2x
·
la relation qui lie « x » à
« y » est 2x +1; on
peut alors écrire f ( x ) = 2x +1
·
la relation qui lie « x » à
« y » est 2x² +1 ; ;
on peut alors écrire f ( x ) = 2x²+1
Cette relation (R.
) devient le deuxième membre de l’égalité : y
= ...R. ... ; que l’on appelle
« équation » (voir
définition du mot : équation).
La valeur de « y » étant
obtenue en fonction d’une valeur donnée à « x » on peut écrire
que :
y
= f(x) = R. (contenant la variable x »)
òlEn écriture mathématique on présente
la « fonction » de la façon
suivante :
Forme générale :
|
f : E x
avec y =
........ |
Lire : Il y a « fonction » de l’ensemble
des nombres E vers l’ensemble des
nombres A où « x » à pour
image f(x) Dans une application : A et E
seront remplacés par des lettres
désignant chacune un ensemble de nombres Et f(x)
sera remplacée par la relation mathématique exprimée en fonction de la variable « x ». |
Exemple :
|
f : R x
|
Lire : Il y a « fonction » de l’ensemble
des nombres Réels vers l’ensemble des nombres Réels où « x » de
l’ensemble de départ à pour image « 2x » dans l’ensemble d’arrivé. Ce
qui permet d’écrire que si f(x) = 2x
alors la fonction aura pour équation « y =2x » Ainsi : f (3) = 6 ; : Alors on peut écrire que :
|
*la relation
« 2x » : cette relation permet de prendre des nombres
dans l’ensemble R et de construire un autre ensemble R ;
Remarque : L’ensemble des
nombres désigné par la lettre R ,
contient tous les nombres dit :
les Réels ( relatifs ;
décimaux ; rationnels ;irrationnels ...............)
|
a) |
f : N x |
La relation est du premier degré : ( forme : linéaire), Ce qui permet d’écrire l’équation y = 2,5x , cette forme sera utilisée pour faire une
représentation graphique dans un repère cartésien. |
|
b) |
f :
N
x |
La relation est du premier degré : ( forme : affine ) Ce qui permet d’écrire l’équation y = 3 x + 2 |
|
c) |
f :
R
x |
La relation est du second degré :l’équation
est y = 2x2 +3x -1 |
Une fonction
peut être représentée par un tableau
Lattention :
il y a quatre modes de représentations utilisés en mathématique
pour « parler » d’une fonction ; Info plus :cliquer ici
)
Dans les exemples
qui suivent les tableaux sont donnés tel quel , on ne connaît pas la
relation qui a permis de le remplir, on veut se
poser la question : le tableau numérique représente - t- il une
fonction ou pas ?
òlTableau
représentant une fonction :
Exemple :1
|
vitesse
en Km/h |
50 |
60 |
70 |
80 |
90 |
100 |
110 |
|
Consommation
en l |
5,4 |
6,2 |
6,9 |
7,8 |
8,7 |
9,3 |
10,1 |
Exemple :2
|
vitesse
en Km/h |
50 |
60 |
70 |
80 |
90 |
100 |
110 |
|
Consommation
en L |
5,4 |
6,2 |
|
7,8 |
8,7 |
9,3 |
10,1 |
Commentaire :
Ces deux tableaux représentent une fonction ,parce que chaque élément (nombre) de l’ensemble de départ (vitesse)
fait correspondre 1 élément (au plus !) dans l’ensemble d’arrivée
(consommation).
òlTableau
ne représentant pas une fonction :
Exemple :3
|
vitesse en Km/h |
50 |
60 |
70 |
80 |
90 |
100 |
110 |
|
Consommation en l |
5,4 |
6,2 |
6,9 /
7.3 |
7,8 |
8,7 |
9,3 |
10,1 |
Exemple : 4 :
|
vitesse en Km/h |
50 |
60 |
60 |
80 |
90 |
100 |
110 |
|
Consommation en L |
5,4 |
6.2 |
6,9 |
7,8 |
8,7 |
9,3 |
10,1 |
Commentaire :
l’élément 70 dans l’exemple 3 et 60 dans l’exemple 4 ont deux images dans l’ensemble d’arrivée, ces deux tableaux
ne représentent pas une « fonction »
« APPLICATION » si il y a « fonction » , il peut y avoir « application »
òRelation entre fonction et application :
Une fonction
est une application si tout élément de l ’ensemble de départ à une image ,et
une seule, dans l’ensemble d’arrivée .
òAttention :Toutes
les fonctions ne sont pas des applications :
òTableau
représentant une application :
Exemple
5 :
|
vitesse
en Km/h |
50 |
60 |
70 |
80 |
90 |
100 |
110 |
|
Consommation
en l |
5,4 |
6,2 |
6,9 |
7,8 |
8,7 |
9,3 |
10,1 |
Commentaire : ce tableau représente une fonction et une
application , à chaque élément de l’ensemble de départ correspond un
élément dans l’ensemble d’arrivée.
òTableau
ne représentant pas une application :
Exemple 6 :
|
vitesse
en Km/h |
50 |
60 |
70 |
80 |
90 |
100 |
110 |
|
Consommation
en l |
5,4 |
6,2 |
|
7,8 |
8,7 |
9,3 |
10,1 |
Exemple 7 :
|
vitesse
en Km/h |
0 |
60 |
70 |
80 |
90 |
100 |
110 |
|
Consommation
en l |
|
6,2 |
6,9 |
7,8 |
8,7 |
9,3 |
10,1 |
Commentaire : les deux
tableaux (6 et 7 ) ne sont pas des
applications parce qu’il manque une image dans l’ensemble d’arrivée.
TRAVAUX
AUTO - FORMATIFS.
1°) Les lettres majuscules N ; D ;
R désignent des ensembles de
nombres ; donner le nom de ces nombres.
2° ) Quelle lettre utilise t - on pour
désigner « une
fonction » ?
3° ) Combien d’ensembles de nombres met en jeu une
fonction ?
4° ) Quel nom donne t - on à ces deux ensembles ?
5° )
Traduire « K
»
6°) Traduire en langage littéral « f(x) »
7°)
Traduire en langage littéral « y K x »
8°) Dites
ce que vous savez sur l’écriture (signification) A = í f(x1) ;f(x2) ;
f(x3) ý
9° )
Traduire : ( quel signification on chaque lettre est signe ?)
v1c1
v1 :.............................................
:.................................
c1 :.......................................................
10°) Idem :
f : V C
f : ......................................
V :.................................
...............................
C ...............................
11° )Qu’est ce qui permet d ’ obtenir limage de
« x » ?
12 °) Quand
dit-on qu’il y a fonction ?
13°) Que
faut-il pour qu’une fonction soit une application ?
14°
)Peut-on dire que toutes les fonctions sont des applications ?
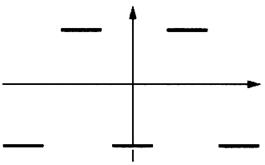
Parmi
ces tracés barrer les représentants d’une non - fonction :
|
Ici : Tracer une non fonction |
|
|
|
|
|
Ici : Tracer une « fonction » |
|
|
|
|
I I ) TRADUIRE :
a)
f : N R
x 2, 5 x
b ) f :
N D
x 3x +2
c)
f : R R
x 2x2 +3x -1
Dire si la relation qui existe entre les éléments
de l’ensemble E et les éléments de l’ensemble F est une
fonction , et une application . Justifier votre réponse .
on donne
x Î E et
y Î F
N°1
|
x |
62 |
79 |
124 |
156 |
163 |
182 |
195 |
|
y |
33 |
45 |
57 |
87 |
96 |
135 |
167 |
N°2
|
x |
62 |
79 |
124 |
156 |
163 |
182 |
195 |
|
y |
33 |
45 |
|
87 |
96 |
135 |
167 |
N°3
|
x |
62 |
79 |
124 |
156 |
163 |
182 |
195 |
|
y |
33 |
45 |
57 |
87 ;135 |
96 |
|
167 |
N°4
|
x |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
y |
7 |
7 |
9 |
11 |
15 |
17 |
19 |
N°5
|
x |
0 |
1 |
2 |
3 |
7/5 |
8 |
2 |
|
y |
2 |
3 |
2 |
5 |
7 |
3 |
5 |