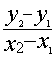Pré requis:
|
Les fonctions et applications (généralités) |
|
|
. |
|
|
L’ensemble des nombres
« réels » : noté par la lettre « R » |
ENVIRONNEMENT du dossier:
|
Objectif précédent : |
Niveau IV : DOSSIER : ETUDES N°2 sur LES FONCTIONS NUMERIQUES
Chapitres :
I)
VOCABULAIRE.
II)
Ensemble de
définition d’une fonction numérique ;
III)
Ensemble d’étude d’une fonction Numérique
IV)
PARTICULARITES D’UNE FONCTION NUMERIQUE.
·
PARITE d’une fonction
- PERIODICITE
- SENS de variation d’une fonction numérique
- Extremum d’une fonction sur un intervalle .
- Applications de la
recherche de l’extremum.
V ) Taux d’accroissement « symbole :
q ( lire Téta)» d’une
fonction numérique sur un intervalle :
|
TEST |
COURS |
Devoir Contrôle |
Devoir évaluation |
Interdisciplinarité |
|
COURS
I)
VOCABULAIRE.
Définition
d’une fonction numérique
« E »
et « F » étant des ensembles numériques , toute correspondance f de
« E vers F » , qui a tout élément « x » de E associe
« au plus » un élément de F est appelée « fonction
numérique » de « E vers F ».
L’image de « x » par f se note f(x) où « x » appartient à E et f(x) appartient à F.
|
Exemples de f :
R |
Nom de fonction : (modèles
types) |
|
x |
|
|
x |
|
|
x |
|
|
x |
|
|
x |
|
|
x |
II) Ensemble de définition d’une fonction numérique : ( Application )
L’ensemble
de définition, noté Df d’une fonction numérique « f » de « E
vers F » est l’ensemble des éléments de « E » qui ont une image
dans « F ».
Exemples à retenir : soit des f : R ![]() R
R
|
Pour « f » |
Le D f est |
Commentaire L On retiendra ces exemples.) |
|
x |
D f = R |
Toutes
valeurs de « x » peut avoir son carrée :Dans ce cas le domaine
de définition est l’ensemble des réels . |
|
x |
D f = R
+ |
La
racine carrée ne s’effectue que sur des nombres positifs.(sont
donc exclues les valeurs négatives) Dans ce cas le domaine de définition est l’ensemble
des réels positifs ou nuls . |
|
x |
D f
= R * Lire :
« R étoile plus » |
« * »
signifie que le nombre « 0 » est exclu.En effet on ne peut diviser
par 0 Dans ce cas le domaine de définition est l’ensemble
des réels non nuls ;on noter aussi :
Df =
R \ |
III ) Ensemble d’étude d’une fonction Numérique
L’ensemble d’étude ( noté If ) d’une fonction numérique f de «
E vers F » est l’ensemble des éléments de Df sur lequel on étudie
la fonction.
Condition :
( If est inclus dans Df
)
Commentaire : If est un
intervalle qui limite l’étude de la fonction .
Les
valeurs de I sont des valeurs numériques appartenant à « x ». la valeur « 0 » est toujours citée soit comme « bornes » soit comme « milieu ou symétrique» .
IV ) PARTICULARITES D’UNE FONCTION NUMERIQUE.
A) PARITE d’une fonction
On doit répondre à la question : est ce que la
fonction est « paire » ou « impaire » ?
1°) Fonction paire : (puissance
« paire »)
Une fonction f de E vers F est dite
« paire » si pour tout « x » pour lequel f(x) existe, f (-x) existe également
et on écrit : f(-x) = f(x)
Dans un repère orthonormal la représentation graphique d’une fonction paire est symétrique
par rapport à l’axe des
ordonnées (axe des « y »).
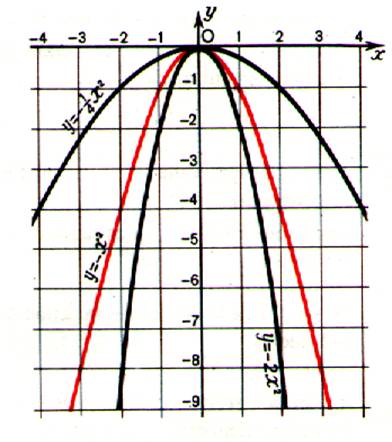
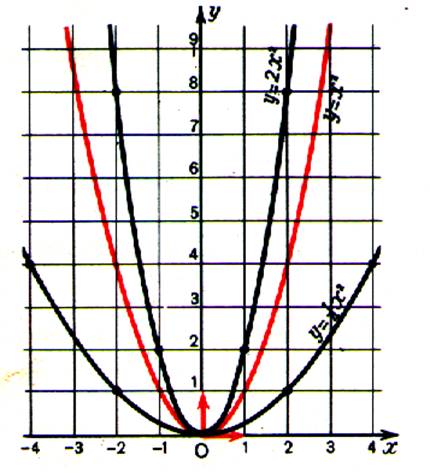
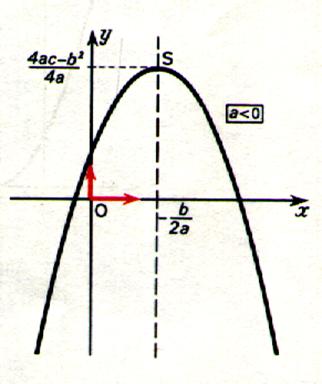
Exemple : la fonction f de R vers R telle que f(x) = a x2 est paire.
|
Sa représentation graphique est une parabole |
|
|
Cas a <
0 |
Cas : a >0 |
|
|
|
2°) Fonction impaire :
(puissance
« impaire »)
Une fonction f de E vers F est
dite « impaire » si pour tout « x » pour lequel f(x) existe , f(-x) existe également et
on écrit : f(-x) = - f(x)
Dans un repère orthonormal la représentation graphique d’une fonction impaire est symétrique
par rapport à l’origine des axes .
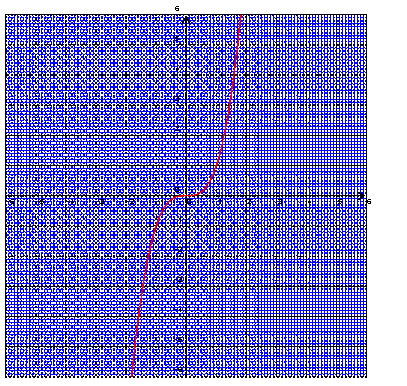
Exemple : la fonction f de R vers R telle que f(x)
= x3 est impaire.
|
|
A)
PERIODICITE :
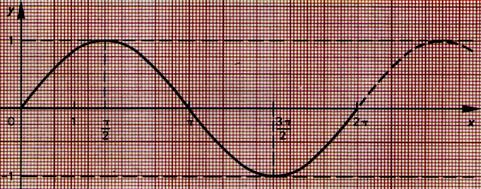
Fonction périodique : (exemple : sinusoïde)
Une fonction numérique f de E
vers F est dite « périodique » et de période T si pour tout « x » pour lequel f(x) existe , f(x +T ) existe également et f(x
+T )= f(x)
( tout multiple d’une période est une période , on réserve
souvent le nom de période de la fonction à la plus petite période positive )
Dans un repère orthonormal ( orthonormé) la
représentation graphique complète d’une fonction périodique se déduit de sa
représentation graphique sur une période par translation de vecteur T![]() .
.
|
exemple :
de sinusoïde
|
C) SENS de
variation d’une fonction numérique :
1° ) Fonction croissante sur un intervalle
Si quels que soient
les réels x1 et x2 distincts de I
,
x2 > x1 entraîne
f( x2 ) ³ f( x1 )
|
|
|
2°) Fonction décroissante sur un intervalle
Si quels que soient
les réels x1 et x2 distincts de I
,
x2 > x1 entraîne f( x2
) £ f( x1 )
|
|
|
3° ) Fonction constante sur un intervalle
Si quels que soient
les réels x1 et x2 distincts de I
,
x2 > x1 entraîne f( x2
) = f( x1 )
Remarques :
Si quels que soient les réels x1 et x2 distincts de I
,
x2 > x1 entraîne f( x2 ) > f( x1 ) , f
est strictement croissante sur I .
x2 > x1 entraîne f( x2 ) < f( x1 ) , f
est strictement décroissante sur I .
« Monotone » :
Si une fonction est (strictement )
croissante ou décroissante sur un intervalle , elle est dite (strictement)
« monotone » sur cet
intervalle.
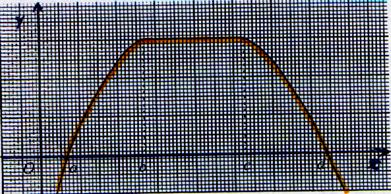
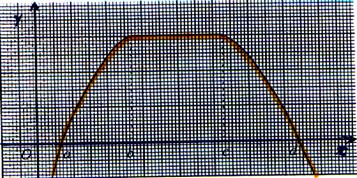
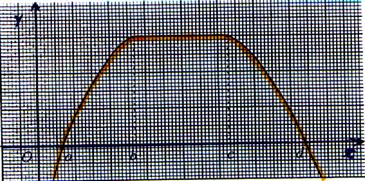
Exemple :
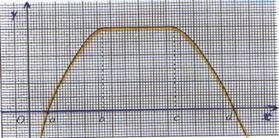
|
Soit fonction f(x) dont on donne la représentation graphique dans un repère
cartésien est : |
|
|
|
|
|
[b c]: |
|
|
|
|
D) Extremum d’une
fonction sur un intervalle .
|
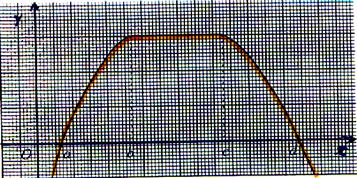
Le point S est le
« maximum » (sommet de la courbe) Soit le point S ( Sx ;
Sy) Sy = f(Sx) est une valeur maximale ou un maximum de f
sur l’intervalle I si pour tout x de I les f(x) < f(Sx) Ou les f(x) < Sy |
|
||||
|
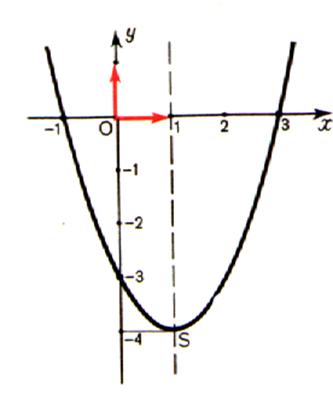
Le point S est le minimum (le point le + bas de la courbe) Soit le point S ( Sx ;
Sy) Sy = f(Sx) est une valeur minimale ou un minimum de f
sut l’intervalle I si pour tout x de I
les f(x) ³ f(Sx) Ou f(x) ³ Sy Ici : S (1 ; -4 ) |
|
Extremum d’une fonction sur un intervalle : Applications
|
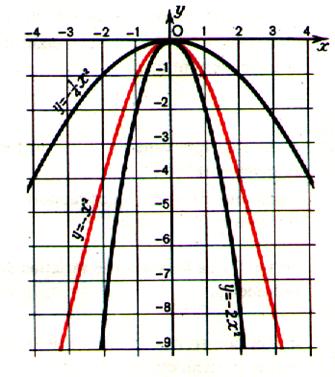
Exemple 1: avec les
fonctions de la forme ax2 avec « a » négatif. Pour la fonction f :
x Elle admet sur R un maximum égal
à 0 pour x0 = 0 Ce qui est vraie pour les autres
représentations graphiques ! ! |
|
|
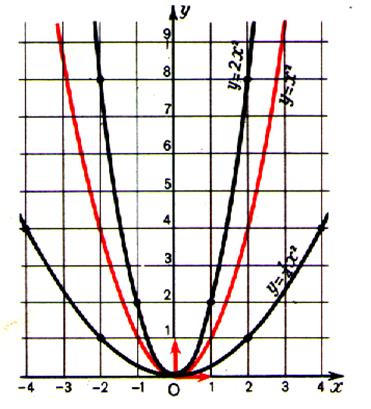
Exemple 2: avec
les fonction de la forme ax2 avec « a » négatif. Pour la fonction f :
x Elle admet sur R un minimum égal
à 0 pour x0 = 0 Ce qui est vraie pour les autres
représentations graphiques ! ! |
|
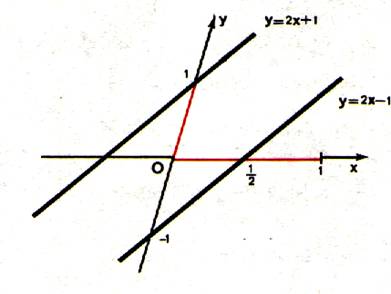
Commentaire : pour savoir si une droite (ou autre ) est
« croissante » ou « décroissante » il faut calculer
son : taux d’accroissement.
|
Taux d’accroissement « symbole : q ( lire Téta)» d’une fonction numérique
sur un intervalle : |
Soit une
fonction numérique f de R vers R dont l’ensemble de définition Df et soit
x1 et x2 deux réels distincts de Df
On appelle
« taux d’accroissement » (ou taux de variation) de f entre x1 et x2 le rapport ![]()
A propos
d ‘écritures :![]() se
note aussi =
se
note aussi = ![]() = q ;
= q ;
sachant que
Dy lire « delta i grec » et Dx est « delta ix » ; Dx représente une
infime partie de « x » soit (x2 - x1 ); Dy représente une infime partie delta
« y ».soit ( y2- y1 )
Calcul de Dy = y2- y1 ;
y2 est obtenu en
f (x2) et puis y1 est obtenu en f (x1) ;
on peut aussi écrire :
Dy = f (x2) - f (x1)
où Dy
peut être remplacé par f (x2 - x1) et Dx peut être remplacer par x2-x1
nous pouvons utiliser indifféremment : ![]() =
= ![]()
|
Exemple : Soit la fonction f : x Résolution : Domaine de définition : Df = R et quels que soient x1 et x2 distincts de Df Calcul de q:
SOS calcul q : 0,5 x22 -
0,5 x12 = 0,5 (x22 - x12) (x22 - x12) est de la forme @Les identités b. Remarquables a 2 - b2 = (a+b)
(a-b) avec « a » =
x2 et b = x1 donc on peut écrire que : (x22 - x12)=
(x2+ x1 )( x2 - x1
) on remplace :
on simplifie :
Exemple : calcul du taux
d’accroissement dans l’intervalle [1 ; 3 ] : Pour x1 = 1 et
x2 = 3 On sait que q = 0,5 (x2+ x1 ) q = 0,5 (3+1 ) q = 0,5 (4 ) q = 2 ( la taux est
positif , dans cet intervalle la fonction est croissante) Faire le même calcul avec des
valeurs négatives : exemple [ -3 ; -1
] (le taux est normalement négatif) |
Représentation
de q
dans la représentation graphique de la courbe :
|
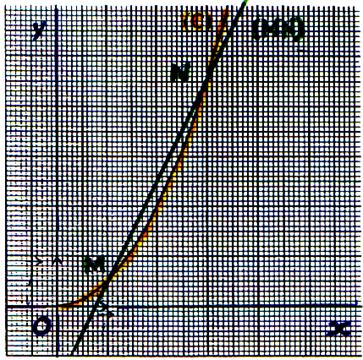
Soit (C ) la courbe représentative de la fonction f dans un
repère orthonormal , q
représente le coefficient directeur de la sécante ( MN) à la courbe ( C ) |
|
q :
Application au sens de variation d’une fonction :
Si
quels que soient x1
et x2 distincts de I :
|
q ³ 0 , f est croissante sur I |
|
|
q = 0 ,
f est constante sur I |
|
|
q £ 0 , f est décroissante sur I |
|
|
Application : |
|
|
|
|
|
le q ³ 0 ,
f est croissante sur [ab]: |
|
|
[b c]: le q = 0 ,
f est constante sur [b c]: |
|
|
Le q £ 0 ,
f est croissante sur [cd]: |
|
Remarques :
q > 0 , f est strictement croissante sur I
q < 0 , f est strictement décroissante sur I
exemple :
Soit la fonction f définie
de R vers R par : f (x) =0,5 x2 est strictement décroissante sur R - (lire R moins) car quels que soient x2 et x1 distincts de R - ; q = 0,5 (x2+ x1 ) est
strictement négatif.
Etant donné une fonction numérique f
de variable réelle « x » , on appelle « courbe représentative de f
dans un repère cartésien » , l’ensemble des points de coordonnées ( x ; f(x))
|
Exemples |
Travaux auto formatifs
Quand dit on qu’ une fonction est « paire » ?
Compléter la phrase :
Donner un exemple de fonction paire :
Quand dit on qu’ une fonction est
« impaire » ?
Compléter la phrase : Dans un repère orthonormal la représentation graphique d’une fonction paire est
……………………
Donner un exemple de fonction impaire :
Compléter les phrases suivantes :
Sur
sens de variation d’une fonction numérique :
A ) Si quels que soient les réels
x1 et x2 distincts de I ,
x2 > x1 entraîne
f( x2 ) ³ f( x1 )
la fonction est ………………………………
B) Si
quels que soient les réels x1 et x2 distincts de I
,
x2 > x1 entraîne f( x2
) £
f( x1 )
la
fonction est ………………………….
C ) Si quels que soient les réels
x1 et x2 distincts de I ,
x2 > x1 entraîne f( x2
) = f( x1 )
la fonction est ………………………….
f
est strictement croissante sur I si …………………………………………
f
est strictement décroissante sur I ………………………………………..
Quand dit-on qu’une
fonction est strictement « Monotone »sur un intervalle I ?:
Reprendre les exercices vus dans le
cours.