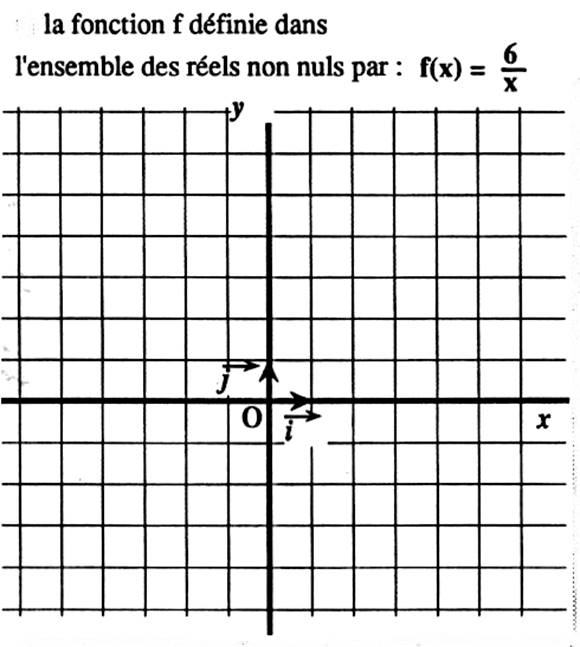
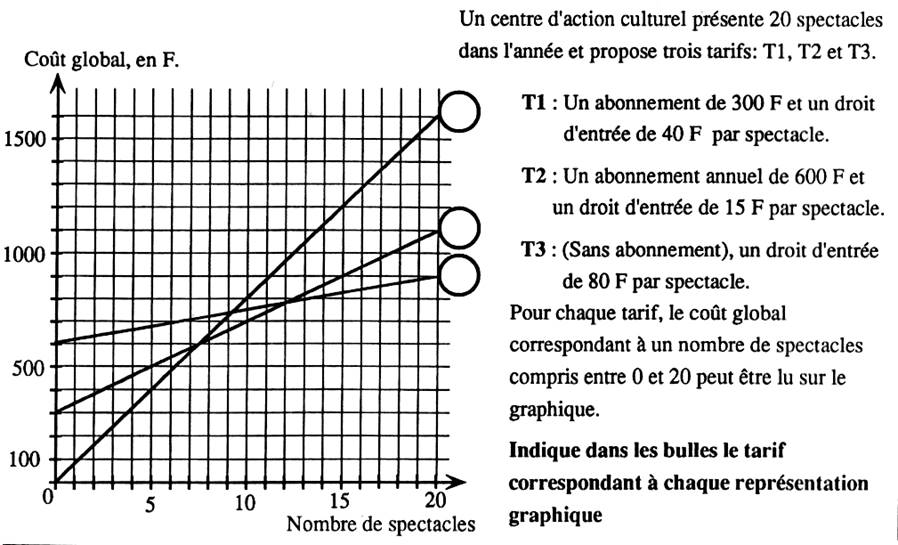
|
DOC : Formation Individualisée |
DOC : Elève. |
|
DOSSIER N° :;Matière : MATH ; Leçon : LES FONCTIONS |
Information « TRAVAUX » ;Cliquer
sur le mot !. |
|
OBJECTIFS :- Savoir tracer des courbes dans un
repère cartésien. |
I ) Pré requis:
|
Notions |
:i |
|
|
Les ensembles de nombres |
||
|
Les tableaux numériques à doubles entrées |
:i |
|
|
Fonction et application |
:i |
|
|
Les repères cartésiens |
II ) ENVIRONNEMENT
du dossier :
|
Dossier précédent : |
Dossier suivant : 1°) L’étude d’une
représentation graphique d’une fonction(niv V) . |
Info : -1° Fonction généralités. |
Savoir construire des courbes dans
un repère cartésien.
Chapitres :
|
i9 |
Rappels
sur les écritures. |
:i |
|
i9 |
Les
principaux tracés. |
:i |
|
i9 |
De la
forme : y = a x ; y = a x + b ; y = a ; x = a ; y = a x² ; y = x3 |
:i |
IV) INFORMATIONS « formation leçon » :
|
Travaux auto - formation. |
|
Corrigé des travaux auto - formation. |
||||
|
Corrigé |
||||||
|
|
|
|
|
|
|
|
V ) DEVOIRS ( écrits):
|
Devoir diagnostique L tests. |
|
|
Devoir Auto
- formatif
(intégré au cours) |
|
|
Devoir Formatif « Contrôle :
savoir » ; (remédiation) |
|
|
|
|
|
Devoir sommatif. |
|
|
Devoir certificatif : (remédiation) |
|
* remédiation : ces documents peuvent être réutilisés ( tout ou partie) pour conclure une formation .
|
|
Leçon |
|
|||||||||||||||||||||||||||||||||||||||
|
|
COURS |
|
|||||||||||||||||||||||||||||||||||||||
|
|
Rappel : Fonction :
notée « f » « x » appelée
« variable ». (ce sera un nombre pris dans un ensemble de
nombres) « f (x) » lire « en fonction de x » Pour
passer de
« x » à « f(x) »
on a besoin d’une relation mathématique : R Cette
relation « R » est une expression
algébrique exprimée avec la
variable « x », cette expression est le deuxième membre de
l’égalité de la forme y = …f (x) Soit l’écriture : x
f (x) La
flèche à talon :
« » doit se
traduire par : «à pour image » x f (x)
lire « ixe » à pour
image « f(x) exemple
soit l’équation « y= 4x »
pour « x = 5
» on trouve « y =
20 » ; f(x) = 20 ainsi
pour 5 20 on lit : pour
«5 » (nombre appartenant aux nombres de l’ensemble de départ) on
obtient « 20 » (nombre appartenant aux nombres de l’ensemble
d’arrivée) exemple
pour : y = 4x
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
On peut prolonger le tableau suivant :
Tracer
dans un premier
repère cartésien : avec |
|
|||||||||||||||||||||||||||||||||||||||
|
|
Les
représentations graphiques types sont de la
forme :
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
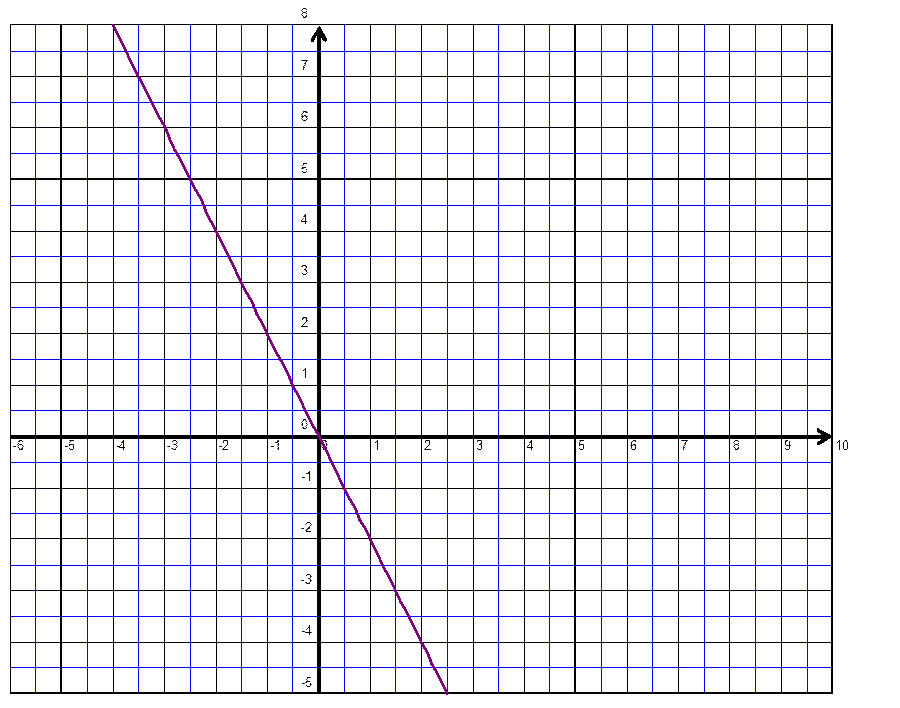
D1
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
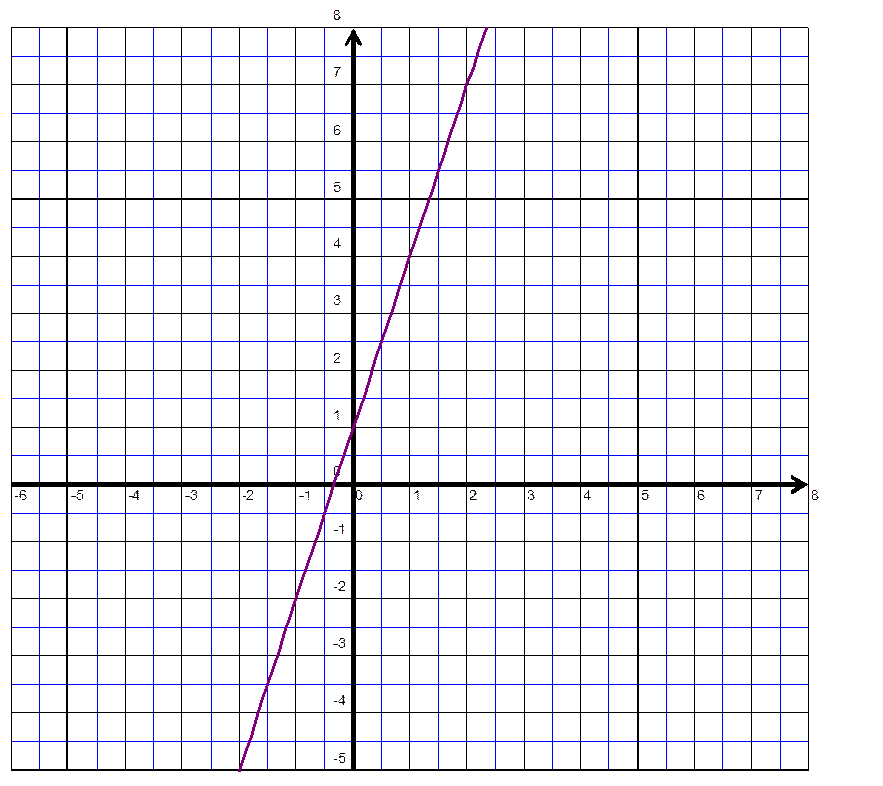
D2 :
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
D3 :
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
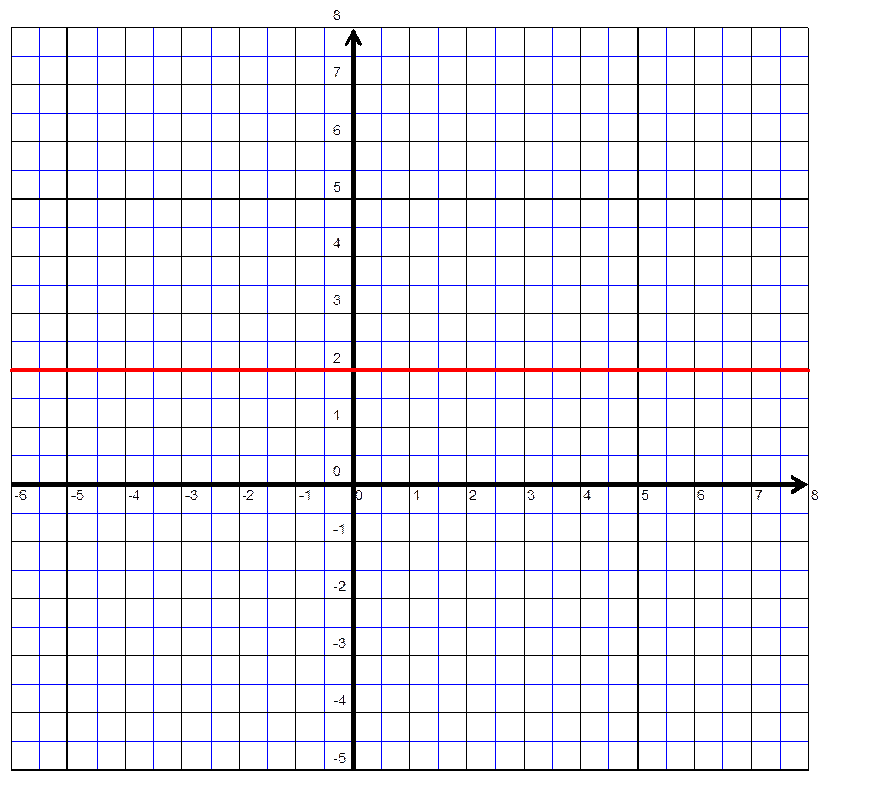
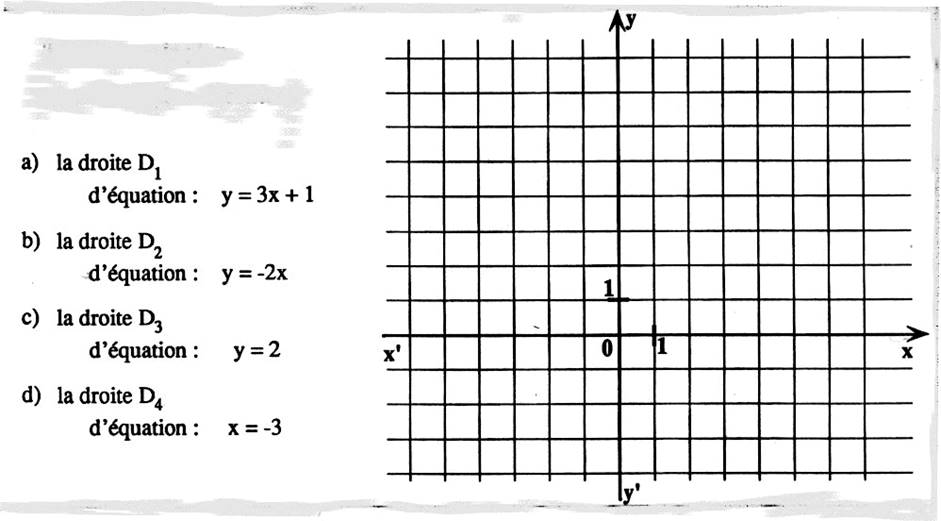
D4 C’est une droite parallèle à l’axe des
« y » |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
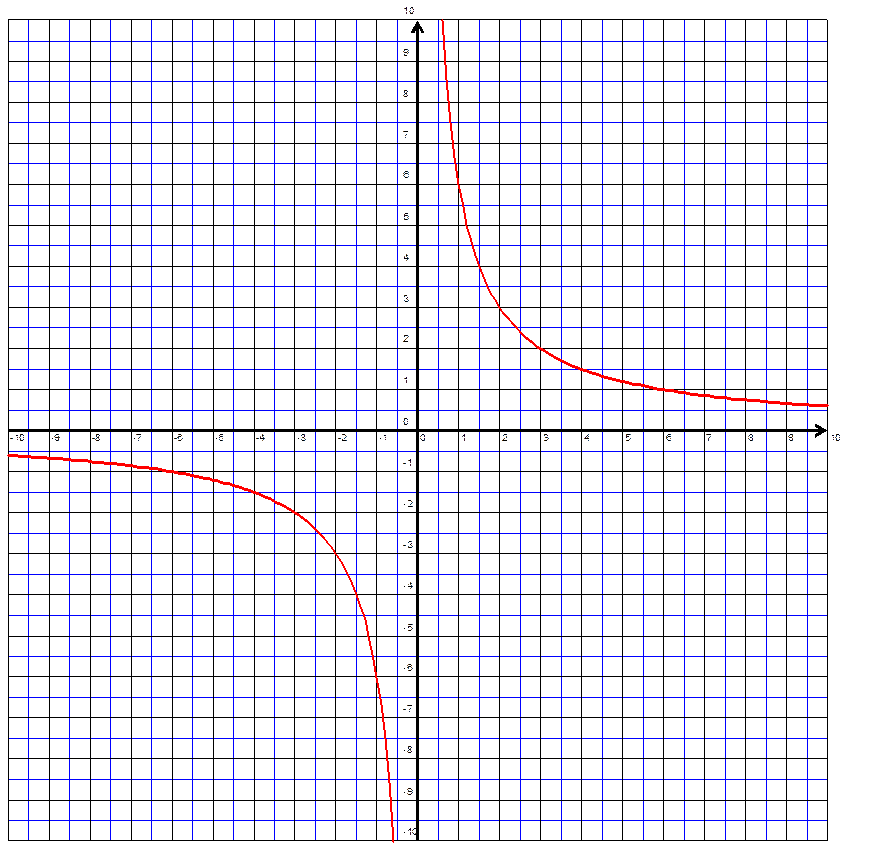
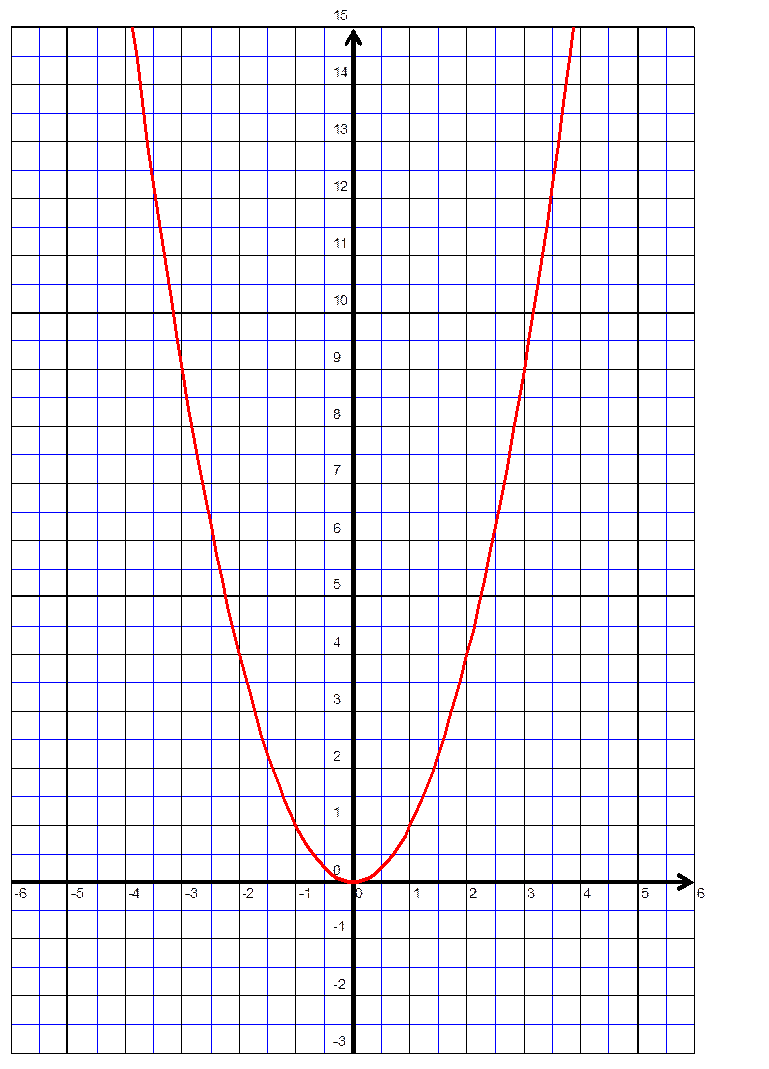
Fonction : |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
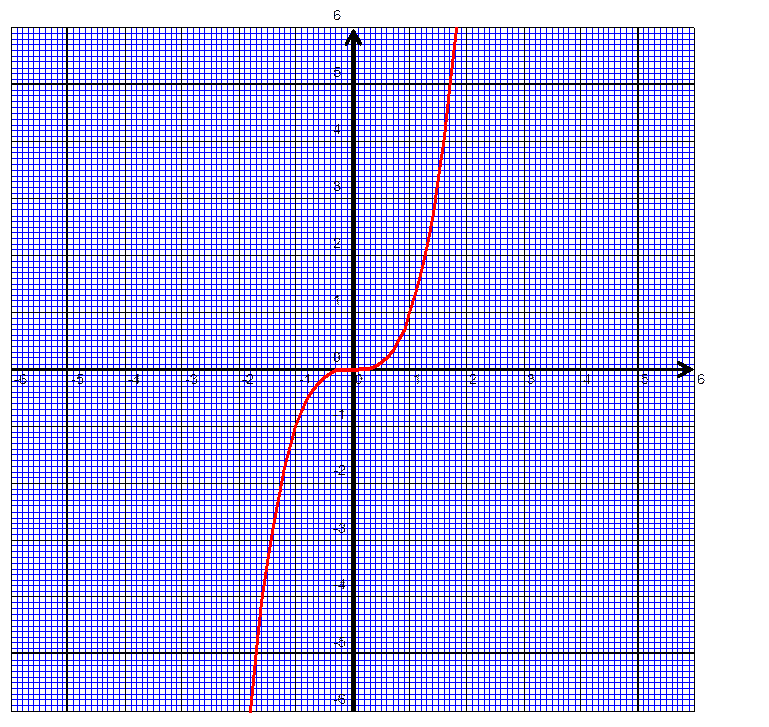
On
remarque que la courbe est symétrique
par rapport au centre « O » |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
Leçon |
Titre |
|
N° |
TRAVAUX d ’ AUTO - FORMATION sur les fonctions. |
TRAVAUX
N° d ’ AUTO - FORMATION : CONTROLE
TRAVAUX
N° d ‘ AUTO - FORMATION EVALUATION
Tracer dans un
premier repère cartésien : avec -![]() et
et
![]()
|
D1
: |
|
|
D2 : |
|
|
D3 : |
|
|
D4 : |
|
Tracer dans une deuxième repère :
|
|
|
|
|
|
|
|
|
|
|
|
DEVOIR :
|
N°1
|
|
N°2
|
|
N°3
|
|
N°4 |
|
|
|
|
|
|
|
|
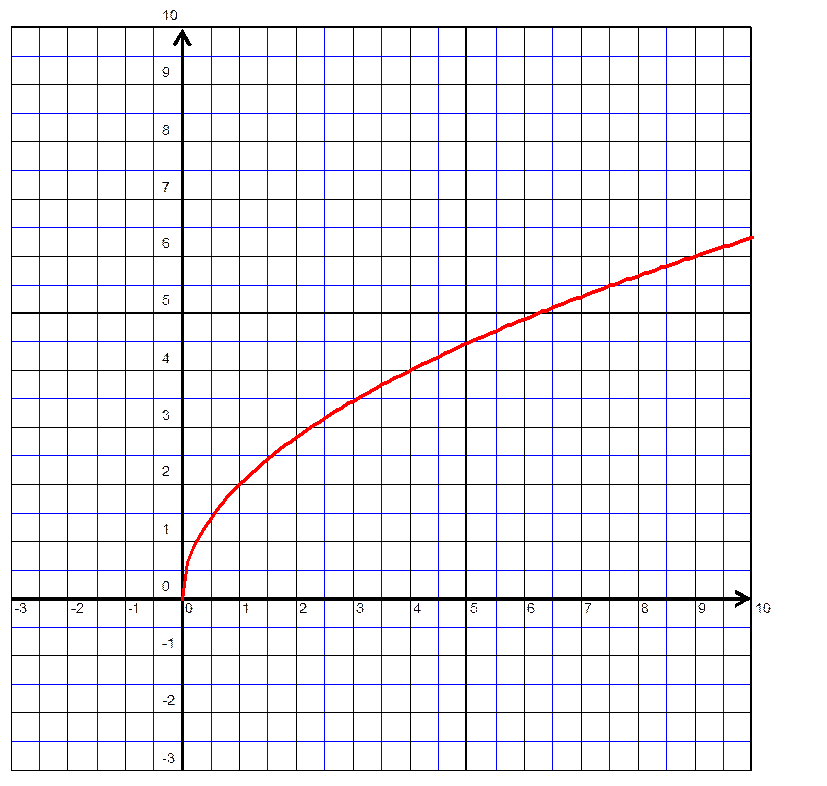
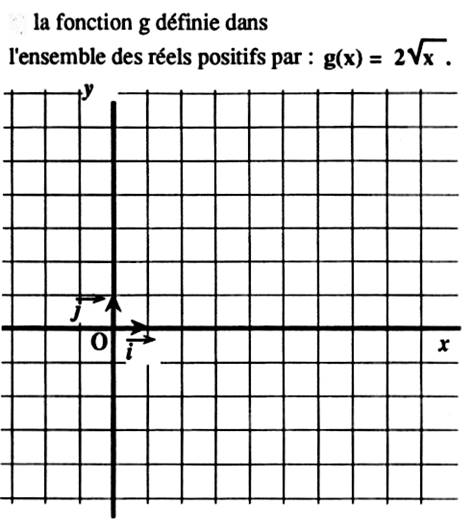
Utiliser les quadrillages ci - contre pour représenter graphiquement la
fonction. Donner le sens de variation de la fonction « g »sur
l’intervalles [ 0 ; 5 ] ……………………………………………………….. « g » est une fonction
…………………………….. Entourer la réponse qui convient et barrer l’autre. Pour les grandes valeurs positives de « x », g(x)
prend des: petites valeurs / grandes valeurs |
|
|
|
|
|
Utiliser les quadrillages ci - contre pour représenter graphiquement la
fonction. Donner le sens de variation de la fonction « g »sur
l’intervalles [ 1 ; 6 ] ……………………………………………………….. « f » est une fonction
…………………………….. Entourer la réponse qui convient et barrer l’autre. Pour les petites valeurs positives de « x », f(x)
prend des: petites valeurs / grandes valeurs Pour les grandes valeurs positives de « x », f(x)
prend des: petites valeurs / grandes valeurs |
|
INTERDISCIPLINARITE.
|
|
|
|
|
|