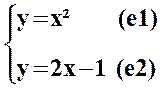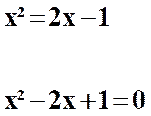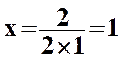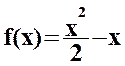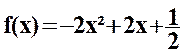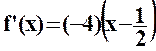DERIVEE.
· I
) NOMBRE DERIVE.
· II
)
FONCTION DERIVEE.
……………….. ( info ++ sur
la fonction dérivée)
· III ) UTILISATION de la dérivée .
Par abus de langage , on dit souvent « dérivée » au lieu de « fonction dérivée ».
La dérivée d'une fonction permet
l'étude simplifiée du sens de variation de cette fonction. La dérivée d'une
fonction permet de déterminer sur quels intervalles de « x », la
fonction f est croissante ou décroissante.
La plan est
rapporté à un repère ortho normal ; La courbe à est la courbe représentative de la fonction
f définie sur R par f(x) = x²
|

|
On a
également représenté sur ce graphique, la droite T d'équation y = 2x - 1.
Le but de
cette activité est de déterminer les coordonnées du ou des points
d'intersection (si ils existent) de
à et T.
Nous
allons donc chercher les coordonnées du (des) point(s) d'intersection de la
courbe d'équation y = x² et de la
droite d'équation y = 2x + 1
|
Les
coordonnées ( x ; y )
des points communs à Ã et T vérifient le système :
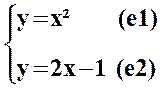
On résout ce
système par substitution en remplaçant y par x² dans (e2) :
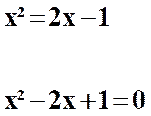
Il faut
résoudre cette équation du second degré :
Le discriminant est : D = (-2) ² - 4 ´ 1 ´ 1 = 4 - 4 = 0
Cette équation admet donc une solution : 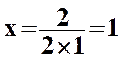
Pour déterminer y on remplace x par 1 dans (e1) (par exemple) donc
y = 1² = 1
Conclusion : Il n'y a qu'un seul point d'intersection de
coordonnées (1 ; 1 ). On dit que la droite T est tangente à la courbe à en A. Le coefficient directeur de la tangente à la courbe à en A est 2 (puisque l'équation
de cette droite est y = 2x + 1) ; On dit que le nombre 2 est le nombre dérivé
de la fonction f pour la valeur x = 1. on écrit : f
'(1) = 2
Il faut
retenir :
Soit ¦ une fonction définie sur un
intervalle I contenant le nombre a et à sa courbe représentative.
On appelle
nombre dérivé de la fonction ¦ en a, le coefficient directeur de la
tangente à la courbe à en son point d'abscisse a. on le note ¦ '(a) (Lire " ¦ prime de a ")
+Exercice n°1
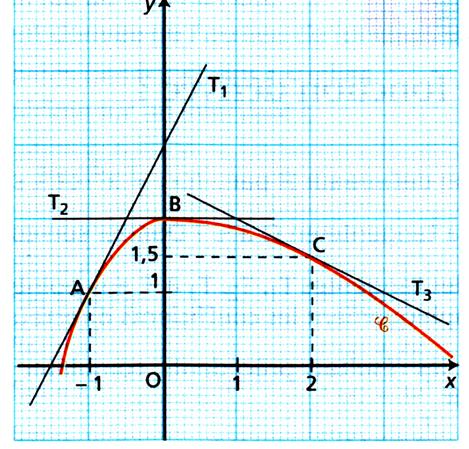
La courbe C est la courbe =représentative d'une fonction f. Les
droites T1? T2 et T3 sont les tangentes à la
courbe C aux points A , B et C.
Déterminer par
lecture graphique les nombres dérivés f '(-1) , f
'(0), f '(2) .
Rappel :
Lorsqu'on se place sur un point appartenant à une droite d'équation y = ax + b, que l'on
augmente l'abscisse de ce point de 1 ( on se déplace de 1 vers la droite),
alors pour retrouver un autre point de la droite il faut se déplacer de a vers
le haut si « a > 0 »
ou de a vers le bas si
« a < 0 »
II )FONCTION
DERIVEE .
Par définition :
On appelle « dérivée d’une fonction » de la variable
« x » , pour une valeur « x O» de cette variable, la pente de la tangente
au point correspondant de la courbe représentative….
Le but de
cette partie est de voir si il n'est pas possible de trouver une
"formule" permettant de trouver directement la valeur de ¦ '(x) pour chaque valeur de x
Soit ¦ la fonction définie sur R par ¦(x) = x² et à sa courbe représentative.
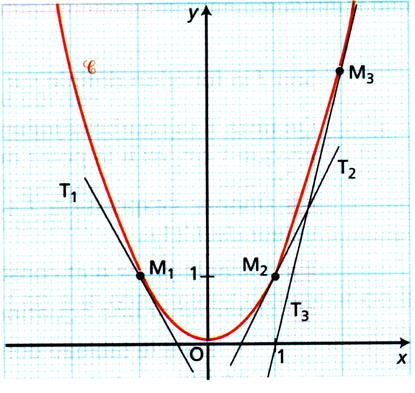
1°) Donner
la valeur du coefficient directeur de la tangente en O à Ã?
2°) On a
tracé les tangente T1, T2 et T3 à Ã aux points M1, M2
et M2 et M3. Déterminer graphiquement les coefficients
directeurs de ces tangentes.
3°) En
utilisant les résultats précédents, compléter le tableau suivant :
On constate
que pour toutes les valeurs de « a »
considérées on a : ¦ '(a) = 2a
Plus
généralement on admet que pour tout réel « x », la fonction ¦ admet un nombre dérivé égal à
« 2 x ».
La fonction
définie sur R par x ® 2x est appelée fonction dérivée
de ¦
On note ¦ '(x) = 2x
Il faut
retenir :
Soit ¦ une fonction définie sur un
intervalle « I ». La fonction qui à tout nombre réel « x »
de « I » associe le nombre dérivée ¦
'(x) est appelée fonction dérivée de « f » .
On la note ¦
' (lire ¦
"prime")
Pour toutes
les fonctions usuelles que vous connaissez, il existe leurs fonctions dérivées
correspondantes, elles sont données dans le tableau suivant : (info
++tableau de calculs de dérivées +)
|
Fonctions ¦
|
Dérivée ¦ '
|
|
¦(x) = a, a réel
|
¦'(x) = 0
|
|
¦(x) = x
|
¦'(x) = 1
|
|
¦(x) = x²
|
¦'(x) = 2x
|
|
¦(x) = x3
|
¦'(x) = 3x²
|
|
¦(x) = 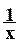
|
¦'(x) = 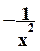
|
Les règles de dérivation sont les suivantes :
Si ¦(x) = u(x) + v(x) alors : ¦'(x) = u'(x) + v'(x)
Si ¦(x) = a ´ u(x) alors ¦'(x) = a ´ u'(x)
Exemple :
+Exercice n°2
Calculer les
dérivées des fonctions suivantes :
¦(x) = 4x² g(x) = x3 + 5x - 2 h(x) = 3x² - 2x + 1
III ) UTILISATION DE LA DERIVEE
L'étude du signe de la dérivée
d'une fonction permet de déterminer le sens de variation de cette fonction.
En effet,
sur un intervalle I de x sur lequel les
tangentes à la courbe représentative de la fonction ont des coefficients
directeurs positifs(ou négatif)( la tangente
"monte" ou la tangente "descend"), alors la courbe
représentative de la fonction "monte"(ou "descend" )
également. On dit que la fonction est "croissante" ou
"décroissante" sur I.
Etudions un
exemple :
La courbe
suivante est la courbe représentative de la fonction ¦ définie sur [-1 ; 4 ] par :
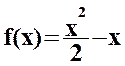
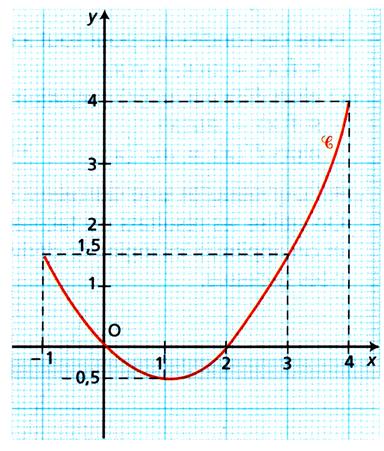
1°) A partir
d'observations du graphique, Indiquer sur quel intervalle la fonction f est
décroissante, sur quel intervalle elle est décroissante.
2°) Calculer
l'expression de f'(x) de la dérivée de f. Etudier le signe de f'(x) sur
l'intervalle [-1 ;
4].
3°) En
utilisant les résultats précédents, compléter le tableau suivant :
|
x
|
-1 1 4
|
|
Signe de
f '(x)
|
0
|
|
Sens de variation de f
|
|
Quelle est la valeur minimale de f? pour quelle valeur de x ?
Pour résumer
:
Si, pour tout x de I, on a ¦'(x) > 0 alors ¦ est croissante sur I.
Si, pour tout x de I, on a ¦'(x) < 0 alors ¦ est décroissante sur I.
Si, pour tout x de I, on a ¦'(x) = 0 alors ¦ est constante sur I.
+Exercice n°3
Soit f la
fonction définie sur [-1 ; 1 ] par 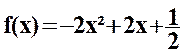
1°)
Calculer la dérivée f '(x) de f.
Vérifier
que 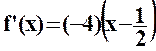
2°) Etudier
sur [-1 ; 1] le signe f'(x). En déduire le sens de variation de f.
3°)
Reproduire et compléter le tableau de variation de f :
|
x
|
-1 1
|
|
Signe de f '(x)
|
|
|
Sens de variation des f
|
|
Cette
fonction possède t-elle un maximum ? quelle est sa valeur
? pour quelle valeur de x ?.