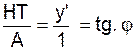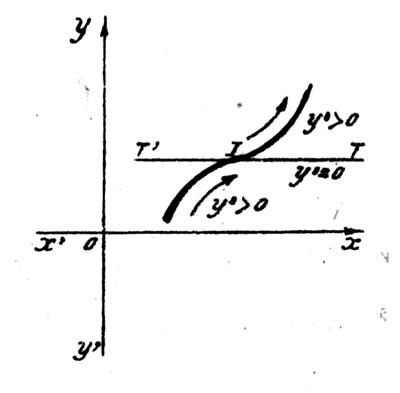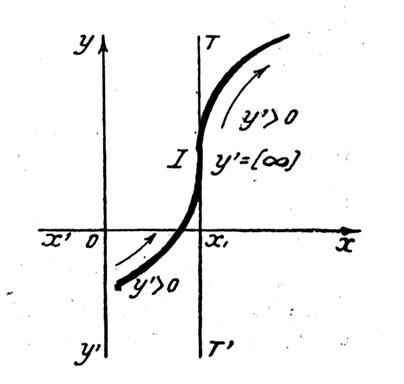|
|
|
Index warmaths |
Objectif précédent 1°)Lecture : notions sur
les dérivées 3°)
signification géométrique de la dérivée |
2°)A voir : Etudes de fonctions :
le second degré. |
|
|
|
|
|
|
DOSSIER sur LES DERIVEES : APPLICATIONS
I)
Tracé de la tangente à une courbe d’équation donnée en un
point donné.
II)
Dérivée : elle
facilite l’étude d’une fonction
III)
Discrimination du maximum
et du minimum ;
IV)
Discrimination du point
d’inflexion et point de rebroussement.
V ) (suite) : Emplois des dérivées pour l’étude de la
variation des fonctions.)
|
Interdisciplinarité |
|
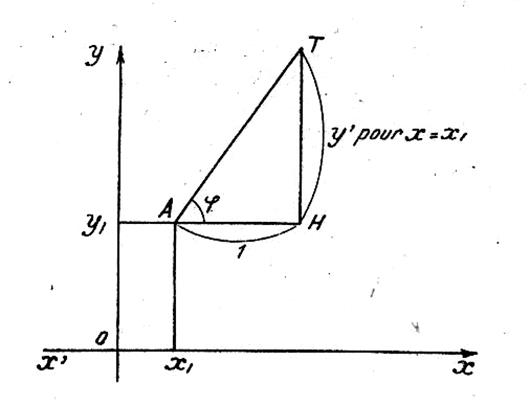
I) Tracé de la
tangente à une courbe d’équation donnée en un point donné ( ►info plus).
Soit « A » le point d’abscisse « x1 »
et d’ordonnée « y1 ».
|
Par ce point, traçons l’horizontale
« AH » égale à l’unité de longueur (= 1 unité
); en « H » élevons une perpendiculaire « HT »
dont la longueur correspond à la valeur de « y ’ » ( appelé :
nombre dérivé ) pour « x = x1 »
et qui est dirigée vers le haut ou vers le bas suivant que cette valeur est
positive ou négative « AT » est la tangente cherchée. On a en
effet |
|
Une courbe étant « encadrée » par ses
tangentes en différents points , le tracé précis d’une
courbe peut être facilité par la détermination de quelques
unes de ses tangentes.
II ) La dérivée facilite l’étude d’une fonction (► info
plus) car elle permet d’en suivre aisément les
variations.
En tout point d’une courbe, la pente est la même que
celle de la tangente en ce point ; il en résulte en résulte que la courbe
et ses tangentes sont simultanément ascendantes, descendantes, horizontales, suivant que la dérivée
« y’ » est positive, négative ou nulle.
Or nous savons qu’une branche de courbe ascendante
est la traduction graphique d’une croissance de la fonction, au contraire une
branche de courbe descendante traduit une décroissante de la fonction.
Il en résulte une corrélation évidente entre le
signe de la dérivée, ses modifications, l’annulation de cette dérivée et
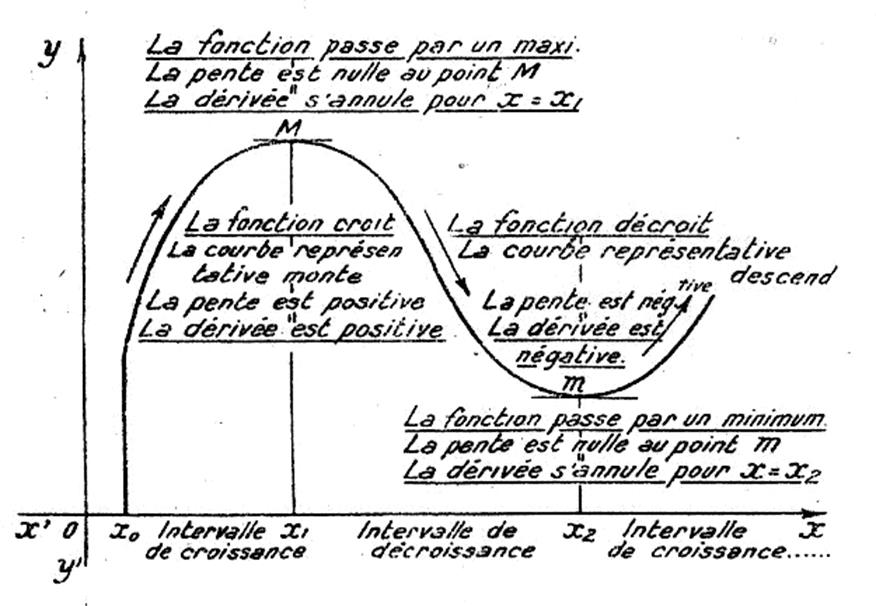
l’évolution de la fonction. Le graphique
ci dessous, dans lequel la courbe « C »
représente les variations d’une fonction « y = f(x) » met en lumière
cette corrélation.
|
|
|
Entre
x0 et x1 la
dérivée est positive :
lorsque la dérivée d’une fonction est positive , pour les
valeurs de « x » comprises dans un intervalle, la fonction est
croissante dans cet intervalle.
Entre
x1 et x2 la
dérivée est négative :
lorsque la dérivée d’une fonction est négative , pour les
valeurs de « x » comprises dans un intervalle, la fonction est
décroissante dans cet intervalle.
En x1
et x2 la dérivée
s’annule :
lorsque la dérivée d’une fonction s’annule , pour la valeur de « x1 » la
fonction passe par un maximum , pour la valeur « x2 » la
fonction passe un « minimum.
III ) Discrimination du maximum et du minimum. (►info
plus)
Un
maximum fait
suite à une « croissance » (dérivée positive) et précède une décroissance ( dérivée
négative) de la fonction.
Un
minimum fait
suite à une « décroissance » (dérivée négative) et précède une croissance ( dérivée
positive) de la fonction.
Donc :
Si
la dérivée est d’abord positive , s’ annule puis devient négative la fonction passe
par un « maximum ».
Si
la dérivée est d’abord négative , s’ annule puis devient positive la fonction passe par un
« minimum ».
L’annulation
de la dérivée sans changement de signe
correspond à un point d’inflexion.
|
|
|
IV) Point d’inflexion ou de rebroussement et « Cas d’une dérivée discontinue »:
Si
pour une valeur « x1 » de la variable « x » , la dérivée « y ‘ » est discontinue et passe par une valeur
infini tg.a = ( ∞) ; a = 90° ; la tangente à la courbe
représentative au point d’abscisse « x1 » est verticale.
Les
cas suivants peuvent se présenter :
Cas
A)
|
Pour
« x = x1 », la fonction « y » est discontinue
en même temps que sa dérivée « y’ ». les deux branches discontinues
de la courbe « y = f (x)»ont une tangente commune verticale ,, d’équation « y = x1 »,
qui les rencontrant en des points infiniment éloignés est une asymptote verticale. Selon
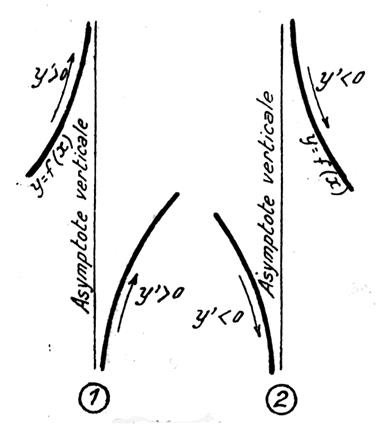
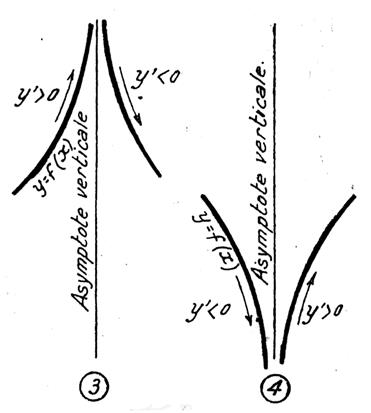
que la dérivée « y’ » change de signe ou ne change pas de signe , de part et d’autre de sa continuité, les branches
discontinues de la courbe « y = f(x) » sont placées comme
l’indiquent les figures ci-dessous. |
|
|
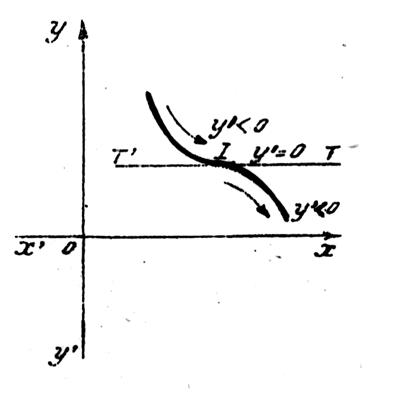
« y’ » ne
change pas de signe. |
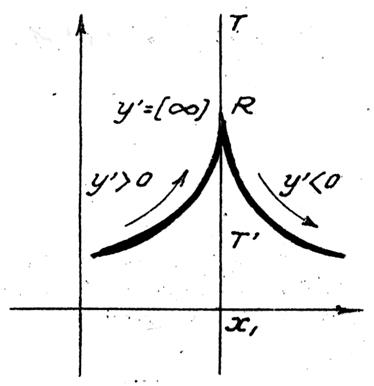
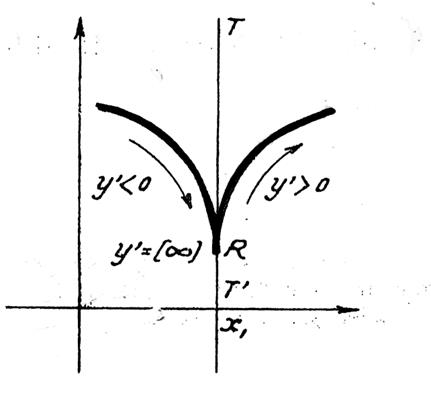
« y’ »
change de signe. |
|
|
|
Cas
B)
Pour « x = x1 », la
dérivée « y ‘» est discontinue mais la fonction « y » n’est
pas continue.
Selon que la dérivée « y’ »
ne change pas de signe ou change de signe, la courbe « y = f (x) »
présente un point d’inflexion à la tangente verticale ou un point de rebroussement.
|
Ci dessous :La dérivée ne change pas de signe ; il y a un point
d’inflexion à tangente verticale. |
|
|
|
|
|
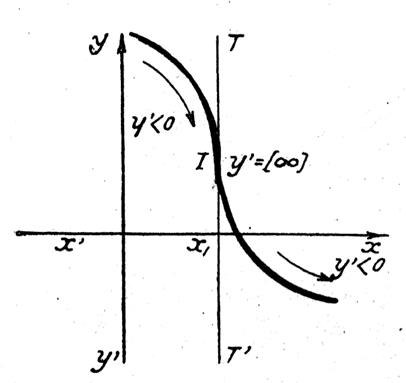
Ci dessous : La dérivée
change de signe ; il y a un point de rebroussement. |
|
|
|
|