|
|
|
|
|
|
|
|
ETUDE DES
FONCTIONS et Application des
DERIVEES à l’étude des fonctions
- Plan d’étude d’une
fonction.
- Recherche des maxima et des minima
- asymptote.
|
Interdisciplinarité
|
|
Plan d’étude d’une fonction
« y =f(x) »
I )
Déterminer , s’il y a lieu, les valeurs de la variable, pour lesquelles la
fonction n’est pas définie, c’est à dire n’est pas calculable ; ces
valeurs sont dites « valeurs de discontinuité » .
A ce sujet se rappeler que : (deux
cas souvent rencontrer)
si f(x) comporte un radical
d’indice pair (
exemple : ![]() ; les valeurs de « x » négatives sont
exclues) « y » n’est pas
calculable pour les valeurs de « x » qui rendent négative
l’expression sous ce radical.
; les valeurs de « x » négatives sont
exclues) « y » n’est pas
calculable pour les valeurs de « x » qui rendent négative
l’expression sous ce radical.
Si f (x)
est un quotient de fonctions de « x » ,
de la forme ![]() , « y »
n’est pas calculable pour les valeurs de
« x » qui annulent
« v » sans annuler « u ». pour des valeurs infiniment
voisines , en plus ( +ξ) ou en moins (- ξ) , d’une valeur de
discontinuité la fonction « y =
, « y »
n’est pas calculable pour les valeurs de
« x » qui annulent
« v » sans annuler « u ». pour des valeurs infiniment
voisines , en plus ( +ξ) ou en moins (- ξ) , d’une valeur de
discontinuité la fonction « y = ![]() » a une valeur infiniment grande ( ∞ ) , le signe
reste à déterminer .
» a une valeur infiniment grande ( ∞ ) , le signe
reste à déterminer .
II )
Calculer les valeurs remarquables suivantes :
- « y » pour « x = 0 » , les termes indépendants de
« x » subsistent seuls, dans le cas d’une fonction algébrique.
- « x » pour
« y = 0 » . On résout algébriquement ou
graphiquement l’équation f (x) = 0
- en cas d’absence d’intervalle fixé : « y » pour « x = ![]() », lorsqu’ une
fonction « y = f(x) s’exprime par un polynôme entier, ordonné par
rapport aux puissances décroissantes de la variable, elle est équivalente à son
terme du plus haut degré pour « x =
», lorsqu’ une
fonction « y = f(x) s’exprime par un polynôme entier, ordonné par
rapport aux puissances décroissantes de la variable, elle est équivalente à son
terme du plus haut degré pour « x =
![]() »,, soit , par exemple, la
fonction : y = a x3
+ b x² + c x + d
»,, soit , par exemple, la
fonction : y = a x3
+ b x² + c x + d
Elle peut s’écrire : 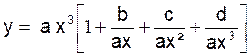
Quand « x » tend vers ![]() les fractions
les fractions 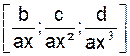 tendent vers zéro,
l’expression entre parenthèse tend vers « 1 », « y »
devient équivalente à son terme du plus haut degré « ax3 ».
tendent vers zéro,
l’expression entre parenthèse tend vers « 1 », « y »
devient équivalente à son terme du plus haut degré « ax3 ».
Si pour « x = x1 » , y = ![]() se présente sous l’une
des formes indéterminées
se présente sous l’une
des formes indéterminées ![]() ou
ou ![]() il est possible de
trouver une autre fraction
il est possible de
trouver une autre fraction ![]() équivalente à
équivalente à ![]() et qui pour « x =
x1 » ne prend plus la valeur indéterminée
et qui pour « x =
x1 » ne prend plus la valeur indéterminée ![]() ou
ou ![]() mais prend au
contraire une valeur déterminée finie ,
infiniment grande ou infiniment petite, appelée « vraie
valeur » de
mais prend au
contraire une valeur déterminée finie ,
infiniment grande ou infiniment petite, appelée « vraie
valeur » de ![]() pour « x = x1 ».
pour « x = x1 ».
Quand on a trouvé la vraie valeur de ![]() on dit « qu’on a
levé l’indétermination ».A cet effet, plusieurs méthodes sont
utilisées : un moyen pratique est l’application de la « règle de l’ Hopital » , que nous
n’énonçons dans ce document.
on dit « qu’on a
levé l’indétermination ».A cet effet, plusieurs méthodes sont
utilisées : un moyen pratique est l’application de la « règle de l’ Hopital » , que nous
n’énonçons dans ce document.
« lorsqu’un quotient de fonction ![]() se présente, pour
une certaine valeur de la variable, sous des formes indéterminées
se présente, pour
une certaine valeur de la variable, sous des formes indéterminées ![]() ou
ou ![]() on obtient sa « vraie valeur » en substituant
à
on obtient sa « vraie valeur » en substituant
à ![]() , le quotient des
dérivées des deux termes
, le quotient des
dérivées des deux termes ![]() ou
ou ![]() ou
ou
![]() jusqu’à ce que
l’indétermination se trouve levée.
jusqu’à ce que
l’indétermination se trouve levée.
Plus simplement : dans ce cas où les deux fonctions « u »
et « v » étant des polynômes
entiers l’indétermination a lieu pour « x = ![]() »,,
on lève cette indétermination en remplaçant « u » et
« v » par leur terme du plus haut degré, par rapport à la variable,
puis on simplifie . La vraie valeur de « y » apparaît alors, égale à
une constante si « u » et « v » sont du même degré par
rapport à « x » ,
»,,
on lève cette indétermination en remplaçant « u » et
« v » par leur terme du plus haut degré, par rapport à la variable,
puis on simplifie . La vraie valeur de « y » apparaît alors, égale à
une constante si « u » et « v » sont du même degré par
rapport à « x » , ![]() si le degré de
« u » est supérieur au degré de « v » , à
si le degré de
« u » est supérieur au degré de « v » , à ![]() si le degré de
« u » est inférieur au degré de « v ».
si le degré de
« u » est inférieur au degré de « v ».
III )
Calculer la dérivée « y’ » puis
les valeurs de « x » annulant « y’ ». Ces valeurs
correspondent à un maximum ou à un minimum pour la fonction ou à un point d’inflexion , à tangente parallèle à l’axe des
« x », pour la courbe représentative. La discrimination de ces
différents cas se fera soit en utilisant la dérivée seconde ,
soit plus couramment , en étudiant le signe de « y’ ». Le signe de
« y’ » s’obtiendra en résolvant
les inégalités « y’ >
0 » et « y’< 0 » soit directement , en remplaçant dans cette
dérivée la variable par des valeurs très voisines , de part et d’autre de cette
valeur d’annulation.
On peut résumé les principaux cas par le
tableau suivant :
|
On
a : |
3
Cas : |
Conditions |
Conséquences |
|
|
y =
0 |
Cas
1 |
Si « y’ passe de
+ à - » |
« y » est le maximum. |
|
|
et « y’’< 0 » |
|
|||
|
Cas
2 |
Si « y’ passe de
- à + » |
« y » est le
minimum. |
|
|
|
et « y’’> 0 » |
|
|||
|
Cas
3 |
Si « y’ ne change pas de signe » |
« inflexion » la tangente à la courbe au point d’inflexion
est parallèle à l’axe des « x ». |
||
|
Et « y’’= 0 » |
||||
|
Départ : |
2
possibilités |
Alors : |
|
« y »
est définie et « y
’ » présente une discontinuité |
« y’ »
ne change pas de signe de part et d’autre de la valeur de discontinuité
. |
« inflexion » - la
tangente à la courbe représentative au point d’inflexion est parallèle à
l’axe des « y ». |
|
« y’ »
change de signe de part et d’autre de sa valeur de discontinuité. |
« Rebroussement »
- la tangente à la courbe représentative au point de rebroussement est
parallèle à l’axe des « y ». |
IV- On résume ces résultats dans un tableau de valeurs auquel on
fait correspondre une courbe représentative.
Recherche des maxima et des
minima :
La recherche des maxima et des minima d’une fonction ne nécessite pas
l’étude complète de cette fonction mais seulement l’application de la règle
suivante :
Pour trouver les maxima et les minima d’une fonction « y = f
(x) » dans un intervalle où elle est continue , ainsi que sa dérivée première
« y ’ » , on pose « y ’ = 0 » et on résout l’équation ainsi
obtenue. Les solutions de cette équation sont les seules valeurs de la variable
pour lesquelles « y » soit maximum ou minimum.
Si pour une de ces valeurs , « y ’ »
de positive devient négative , « y » est maximum , si
« y’ » de négative devient
positive , « y » est minimum.
Si « y ’ » s’annule
mais ne change pas de signe « y » n’est ni maximum , ni minimum.
On peut également faire la discrimination entre le maximum et le minimum
en considérant le signe de la dérivée seconde
« y ’’ »
« y’’ » est négative pour une valeur de la variable
correspondant à un maximum de « y » , elle
est positive pour une valeur de la variable correspondant à un minimum de
« y ».
(voir des exemples)
Les asymptotes aux branches de
la courbe représentative sont de trois sortes :
« asymptote » verticale , asymptote
horizontale ; asymptote oblique.
En principe :
(1)
si la fonction est discontinue pour « x = a » il y a une
asymptote verticale parallèle à « y y’ »
d’équation « x = a ».
(2)
Si la fonction a pour vraie grandeur « y =b » pour
« x = ![]() » , il y a une asymptote horizontale
parallèle à « x x’ » d’équation « y =
b ».
» , il y a une asymptote horizontale
parallèle à « x x’ » d’équation « y =
b ».
(3)
Cliquer ici pour savoir comment on détermine une asymptote oblique.
CONTROLE : aucun
travail de prévu.
Savoir
énoncer les règles.