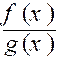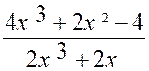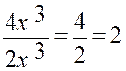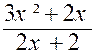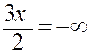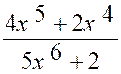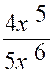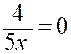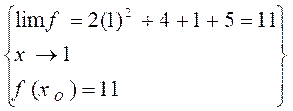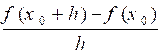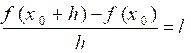ENVIRONNEMENT du dossier:

INDEX   : warmaths

Objectif précédent  1°)  Notions 2°) Les fonctions (présentation)  3°) Les fonctions numériques 4°) Généralités sur les fonctions numériques.

Objectif suivant : 1°) Etude sur l’étude de la représentation graphique d’une fonction 2°) Etude des fonctions usuelles  3°) Les fonctions numériques (niveau 4) 4°) Les fonctions numérique et la dérivation.

Tableau        4.02 Sommaire sur les fonctions.   1°) Les fonctions niveau V B EP . 2°) Le second degré niveau V BEP 3°) Les tracés BEP

 

RESUME  sur  L’ETUDE D’ UNE FONCTION NUMERIQUE.

 

1.     Marche à suivre pour étudier une fonction : (procédure)

2.    Domaine de définition.

3.      Les Limites

4.    Opération sur les limites (d’une somme ; d’un produit ;d’un quotient ; d’un polynôme ;d’une fonction rationnelle…)

5.    Continuité  (en 1 point ; sur un intervalle)

6.    Cours suivant :   Dérivée : (dérivée en 1 point ; fonction dérivée d’une fonction ; signe de la dérivée et sens de variation de la fonction ;extremums locaux ;

 

 

 

 

 

 

 

 

 1 - Marche à suivre pour étudier une fonction : (procédure)

 

On procédera en suivant l’ordre suivant :

	1°)  Recherche du domaine de définition.	@ Info plus.
	2°)  Recherche des limites aux bornes du domaine de définition.	@ Info plus.
3°)  Cours suivant :
	1.      Calcul de la dérivée pour déterminer les divers sens de dérivation de la fonction ( tableau de variation)	@ Info plus.
	2.    Calculs des extremums locaux	@ Info plus.
	3.     Graphique (représentation)	@ Info plus.

 

 

1       -  Domaine de définition.

 

Etudier la définition d’ une fonction numérique , c’est déterminer pour quelles valeurs de la variable ( x ) il est possible de calculer la valeur numérique correspondante de la fonction  ( y)  

 

En étudiant la définition d’une fonction , on définit le domaine de définition de cette fonction.

 

Notation     D f   ;      Si la fonction est notée «f » 

 

 

Il est nécessaire de déterminer le domaine de définition d’une fonction dans les 4 cas suivants (Dans les autres cas le domaine de définition sera    R   (ensemble des réels)       

 

Cas 1 :  Pour la fonction du type :   f (x)  =             ( ou mu « μ »  est un polynôme) ;      « μ »  doit être différent de zéro ( 0) , donc  toutes les valeurs de « x » qui annulent « μ » doit être exclues de             

       R   (ensemble des réels)  .

 

 

Exemple : Déterminer le domaine de définition de la fonction :     f (x)  = 

 

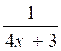
On résout :  4 x + 3 = 0                    x  = 

D’où le domaine de définition de la fonction est : 

D f   =  ]  -   ;     [ u ]   ; +  [      ou   écrit différemment       R  - 

 

 

Cas 2 :  Pour la fonction  du type f (x)  = ; (lire : racine carrée) ;   « μ »  doit être  positif  , donc    0  ( car une racine carrée   ()   ne peut être négative ) 

 

Exemple : Déterminer le domaine de définition de la fonction :     f (x)  = 

 

On résout   :  4 x + 3    0                    x    

D’où le domaine de définition de la fonction est : 

 

D f   =  [       ;  +    [ 

 

Cas 3 :  Pour la fonction  du type f (x)  =   tangente  ou cotangente   ; voir cours sur la  trigonométrie .

 

 

 

Cas 4 :  Pour la fonction  du type f (x)  =   ;  avec     u  doit être    0     et   v   doit être   >  0    ;    

 

 

Exemple :   Déterminer le domaine de définition de la fonction :     f (x)  =  

 

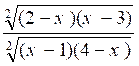
Pour que cette fonction soit définie ,il faut que :

( 2 – x) ( x – 3)    0     et   ( x – 1)(4 – x)    >  0

 

 

On résout :

	2 – x    0        x   2		x -  1 > 0       x   > 1
	x – 3    0        x   3		4 – x  >  0       x  <  4

 

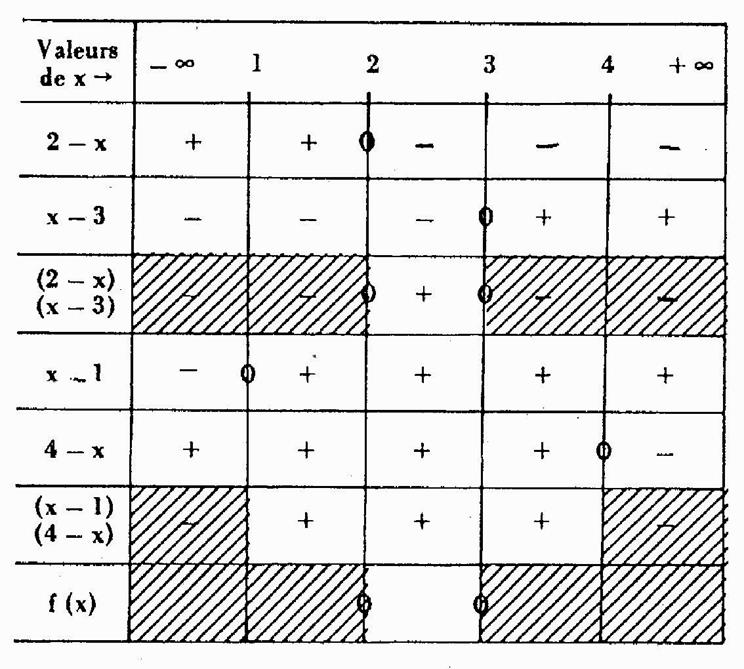
Pour trouver les valeurs de « x » qui rendent positives ces polynômes , on utilisera  un tableau :

Les zones hachurées correspondent   aux valeurs de « x »   qui sont exclues du domaine de définition. Ces valeurs rendent le polynôme sous le radical négatif ……

Les plus «+ » quand les valeurs de « x » sont positive et les moins ( - )  quand les valeurs de « x » sont négatives.

 

                                                

la dernière ligne hachurée , représente la superposition des 2 zones précédentes et permet de déterminer dans quel intervalle , les valeurs de « x » ne rendrons jamais les deux polynômes négatifs.

 

 

 

2 – LIMITES.

 

 

Prenons par exemple la fonction :   f (x)  =                 (@ info plus)                           

 

D f   =  ]  -   ;  0   [ u ]  0 ; +  [      ou   écrit différemment       R  - 

 

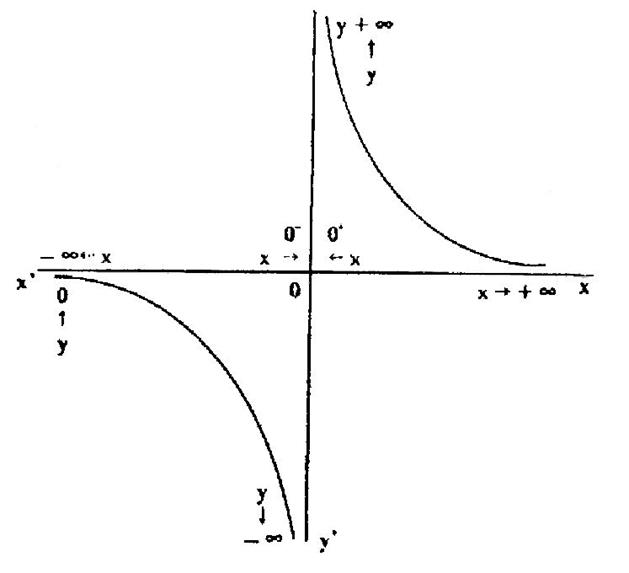
Traçons la représentation graphique de cette fonction :

 

On remarque que :

Quand « x » diminue ; « y » tend vers 0    lim  f (x)   =  0   Quand « x » augmente    ; « y » tend vers 0    lim  f (x)   =  0   ;   x       Quand « x » tend vers 0   par valeur inférieure  ; « y » tend vers   -      lim  f (x)   = -   ;   Quand « x » tend vers 0   par valeur supérieure « y » tend vers   +      lim  f (x)   = +  ;     Nous devons remarquer que l’étude des limites se fait au voisinage des bornes de l’ensemble de dfénition.

 

3- OPERATIONS  SUR LES LIMITES.

 

 

Limite d’une somme :

 

Lorsque « x » tend vers  x_O  ou  

 

Si « x » tend vers	a	a	a
Et si  g (x) tend vers :	b
f (x)   +   g (x)             tend vers	a   + b					?

 

 

Limite d’un  produit :

 

Nous supposons connu le signe de chacun des facteurs  f (x)  et   g (x)      et  nous donnons seulement la valeur absolue de ces facteurs ou de leur produit lorsque cette valeur absolue est infinie.

 

Lorsque « x » tend vers  x_O  ou  

 

Si « x » tend vers	a	a 0		0
Et si  g (x) tend vers :	b
f (x)     g (x)             tend vers	a  b			?

 

 

 

 

 

Limite d’un  quotient  :

 

Nous supposons connu le signe de chacun des facteurs  f (x)  et   g (x)      et  nous donnons seulement la valeur absolue ou celle de leur quotient  lorsque cette valeur absolue est infinie.

 

Lorsque « x » tend vers  x_O  ou  

 

Si « x » tend vers	a		a 0	a	0
Et si  g (x) tend vers :	b 0	b 0	0*		0
f (x)   /  g (x)     ;          tend vers				0	?	?

 

Limite d’un polynôme :

 

Rechercher  la limite d’un polynôme lorsque « x » tend vers  + ou – l’infini  ( )  , équivaut  à rechercher la limite du terme du plus haut degré lorsque x  vers

 

 

Exemples :

 

lim   2 x³ + 4 x² + 2 x – 4                      lim   2 x³     = 

x                                                   x 

 

lim   4 x ⁵ + 5 x⁴ + 2 x – 4                      lim   4 x ⁵     = 

x                                                    x 

 

Limite d’un fonction rationnelle  :

 

La limite d’une fonction rationnelle, lorsque x devient infini , est celle du quotient des termes de plus haut degré de son numérateur et de son dénominateur.

 

Exemples :

 

lim			lim
x			x

 

 

lim			lim			lim
x			x			x

 

lim			lim			lim
x			x			x

 

CONTINUITE

 

a)  Continuité en un point .

 

Soient   x_o , a , b des réels tels que   a < x_o <  b  .On considère une fonction f   définie sur un ensemble  D  contenant  ] a ; b [

 

On dit que la  fonction f   est continue en  x_o   si et seulement si :

      

-        la limite quand x tend vers x_o  existe ,

-        lim  f  =  f (x_o)

-        x     x_o

 

Cela équivaut à 

lim  f	= lim  f	=  f (xo)

 

-        Exemple :        f (x)     =  2 x ²  + 4 x + 5      ;  Continuité en   x_o  =  1

 

		Lim   f  existe
		x 1		La fonction f est continue en xO  = 1
		lim f  =  f (xo)
		x 1

 

b )  Continuité sur un intervalle.

 

On dit que f  est continue sur ] a , b [  si f est continue en tout  x_o  élément de  ] a , b [ ,

 

Théorème :

-        Toutes fonctions polynômes est continue sur  R .

-        Toute fonction rationnelle est continue sur son domaine de définition.

           

 

Cours suivant :   Dérivée : (dérivée en 1 point ; fonction dérivée d’une fonction ; signe de la dérivée et sens de variation de la fonction ;extremums locaux ;

 

Dérivée en 1 point .

 

Soit  x0  un élément d’un intervalle  ] a , b [  . On considère une fonction  f  définie sur un ensemble  D  contenant  l’ intervalle  ] a , b [. Soit  « h » un réel, on appelle « dérivée de f    pour x = x0 » la limite ;si elle existe ;  du rapport :      quand  « h » tend vers 0 .

 

lim
h 0

 

Notation :        y ₀’    ou   f ‘  ( x₀)

 

 

Interprétation graphique :

Pour qu’une fonction y = f( x )  admette en x₀  une dérivée , il faut et il suffit que la courbe représentative admette au point d’abscisse x₀ une tangente ( non parallèle à 0y )

 

Le coefficient directeur de cette tangente est égal à la dérivée de la fonction pour   x = x₀ 

 

 

Voir : l’ équation de la tangente :  y =  f ‘ ( x₀ )  .  ( x – x₀ ) +  f ( x_O)