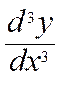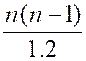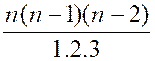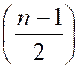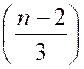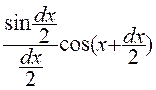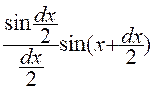Pré requis:
|
« Factoriser » et
« développer » |
|
|
|
|
|
Calcul
numérique (calculs avec des relatifs contenant des carrés) |
|
|
|
|
|
|
|
Index warmaths |
Objectif précédent
|
1°)Les dérivées |
|
|
|
|
|
|
DOSSIER:
Compléments sur les , NOTIONS sur
« les dérivés »
1.
La règle de trois : limites de son domaine ;
2.
Essai pour étendre ces limites :
3.
Intérêt que représente l’étude de la
dérivée dérivées
4.
RECHERCHE DES DERIVEES :
1. DERIVEE SECONDE .
2. DERIVEE
TROISIEME :
3.
DERIVEES SUCCESSIVES. (
Application : Formule
du binôme) .
5 . DERIVATION
INDEFINIE : EXPRESSIONS
ALGEBRIQUES à PUISSANCES
NEGATIVES.
·
DEVELOPPEMENT DE
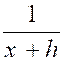en série
. ( d’ après la formule de Taylor)
·
et Fonction y =
sin. x ( Autre
exemple de dérivation indéfinie ).
|
|
|
Devoir
évaluation |
Interdisciplinarité
|
|
Corrigé
Contrôle |
Corrigé
évaluation |
Les langages utilisés pour exprimer une étude de
problème :
Exemple : Un
ouvrier gagne 1 € par heure.
Combien gagne - -t – il en 2 ; 3 ; ….. « x » heures ?
Modèles utilisés :
a) Le
Tableau :
|
Nombres « x » d’heures |
1 h |
2h |
3 h |
……. |
x h |
|
Gain « y » |
1 € |
2 € |
3 € |
……. |
x € |
b) l’équation : Le gain est inscrit dans le
tableau ; il est y = x ; il dépend du nombre d’ heures de
travail ; il est fonction de « x ».
c ) Le graphique :
représentons- le graphiquement la situation .
|
|
|
|
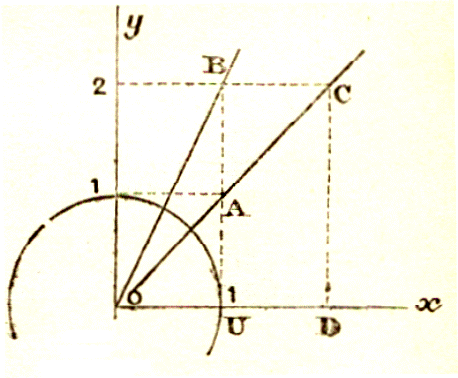
Au point U
pris sur Ox , tel que OU = 1 heure , prenons l’ordonnée UA = 1 Euro
. Le gain est figuré par la droite OA.
Cette droite pour le point D (
tel que OD = 2 heures ) a pour ordonnée
DC = 2 Euros . Etc. ;…..
Nous avons exprimé le gain de l’ouvrier en trois langages :
1°) par le tableau ,
arithmétiquement ;
2°) par la droite OA ,
graphiquement ;
3°)par l’équation y = x ,
algébriquement.
Suite : un autre ouvrier gagne 2 € , par heure . Combien gagne –t- il en « x »
heures ?
Son gain peut – être représenté par le tableau
ci-dessous :
|
Nombres « x » d’heures |
1 h |
2h |
3 h |
……. |
x h |
|
Gain « y » |
2 € |
2 |
3 |
……. |
x |
Il l’est aussi par l’ équation : y = 2x
Il l’est aussi par la droite OB ( voir figure
précédente) , telle que pour OU = 1 l’ordonnée soit UB = 2
Ce qui distingue le gain des deux salariés
c’est :
Dans le tableau :
La première
ligne : l’heure
Dans l’équation :
Le coefficient
de « x » : 1 pour le salarie A et 2 pour le salarié B
Dans la représentation graphique :
pour une même abscisse « OU » on a l’ordonnée « UA » pour le salarié A et
l’ordonnée « AB » pour le salarié B
L’angle AOU est caractérisé par le rapport 
=
que l’on appelle « tangente 
»
L’angle BOU est caractérisé par
le rapport 
=
que l’on appelle « tangente 
»
Ce rapport appelé « tangente de l’angle » est
en effet la longueur de la tangente
au cercle
de rayon OU = 1 , menée par le point U et limitée par
la droite considérée ( droite OA , 1er cas , droite OB 2e
cas ).
Cette tangente
( ou )
, ce coefficient de « x » dans
l’équation de la droite ( y = x
ou y = 2x ) s’appelle encore « coefficient angulaire de la droite » ou « pente de la
droite ». »
Règle de trois : ( ces limites)
La ligne droite de la représentation graphique ,
l’équation de la forme y = ax du premier degré , les tableaux de grandeurs proportionnelles
, régissent de la même manière bien que sous trois forme s différentes , la
très grande majorité des problèmes abordés à l’école primaire , régissent le
« fameuse » règle de trois .
Dans le tableau , si l’on prend deux
lignes portant les nombres x’ et y’ pour
l’une et x’’ et y’’ pour l’autre
|
Nombres
« x » d’heures |
1 h |
2h |
3 h |
x’ |
x’’ |
|
Gain « y » |
2 € |
2 |
3 |
y’ |
y’’ |
on a : 
= 
;
par extension on a 
=
connaissant trois de ces nombres
, on peut calculer
le quatrième .
D’après
l’équation y = a x , on peut pareillement écrire
y’ = a x’ et y’’= a x’’ d’où on déduit 
=
et on obtient
la même relation ; la même règle de trois à employer . règle de
trois à employer .
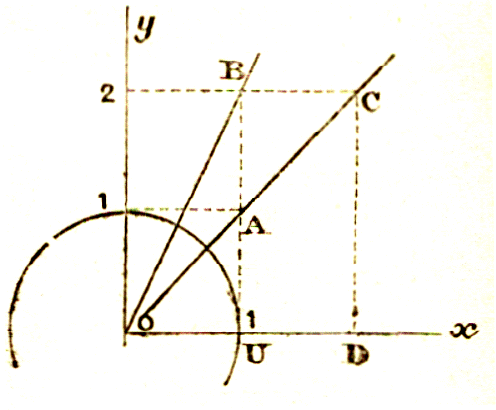
Enfin , d’après le graphique , si on prend sur la
droite deux points A et C (voir graphique)
Qui ont pour ordonnée et pour abscisse :
pour le
point A l’abscisse l’un OU et l’ordonnée
AU et pour le point B l’ abscisse OD
et l’ordonnée CD , on
aura :
= 
c’est à dire encore =
( voir les
triangles homothétiques et le
rapport d’homothétie)
Cette règle de trois se rencontre si souvent dans les problèmes posés à
l’école primaire et au collège qu’il
arrive qu’elle soit appliquée automatiquement sans réflexion par les
élèves.
Il est bon de bien comprendre qu’en procédant ainsi on risque des
erreurs très graves en fait et en théorie .
Qu’on se garde de croire que , en fait , une douzaine d’objets coûte ,
de toute nécessité logique , 12 fois plus qu’un seul objet . A plus forte
raison , qu’on se garde de croire qu’une pierre dans sa chute en 2 secondes
parcourt seulement 2 fois plus de chemin qu’en une … ; etc. .
Il y a des grandeurs liées par
proportionnalité , c’est à dire , il y a des droites , c’est à dire il y a des
équations du 1er degré. Mais il y a aussi des courbes, il y a des
équations plus compliquées ; il y a des grandeurs liées par des relations
moins simples que la proportionnalité directe.
Question : Dans quel cas la règle de trois
est-elle applicable ?
Un ouvrier gagne 4 € à l’heure . Son gain en « x »
heures est y = 4 x
Ou bien , un piéton fait
Gardons ce dernier cas ( celui du piéton) et
comparons l’accroissement de la
fonction « y » ( du chemin parcouru ) à l’accroissement de la
variable « x » ( de la durée du trajet ).
Supposons un premier trajet durant « x »
heures ; sa valeur est « y »
Relation
équation 1 y = 4 x
Supposons un
deuxième trajet , durant ( x + Dx ) heures :
La notation Dx représente la différence entre la nouvelle
valeur (t2 )et la première valeur de la variable « x » (t1) ; ainsi (
t2 - t1 = Dx)
Le nouveau trajet est ( y + Dy ) kilomètres ; (Dy est la distance
parcourue pendant l’instant t2
- t1 = Dx , elle
représente la différence entre la nouvelle valeur et la première valeur de la
fonction (y) . ainsi Dy = 4 Dx )
On a :
Relation équation 2 y + Dy = 4 ( x + Dx )
Nous voulons comparer Dy et Dx
En
retranchant membre à membre les
équations (1) et (2)
y + Dy = 4 (
x + Dx
) et y
= 4 x
premiers membres : y +
Dy – y = Dy
deuxièmes membres 4 ( x + Dx ) -4 x
= 4 x – 4x +4 Dx = 4 Dx
nous avons
Dy = 4Dx ou
= 4 =
une « constante »
Ce rapport ,ici, c’est la vitesse du piéton ;
c’est le chemin parcouru à chaque
nouvelle heure ( de 0 h à 1 h ; de 1 h à 2 h , … ).
Les grandeurs « y » et « x »
ici sont proportionnelles parce que la vitesse
est constante .
Cette vitesse est « 4 » ; c’est le
coefficient de « x » dans l’équation fondamentale « y = 4
x » . Donc , les grandeurs
sont proportionnelles parce que l’équation qui les lie est du 1er degré .
Ou enfin nous pourrons traduire cette
condition géométriquement
|
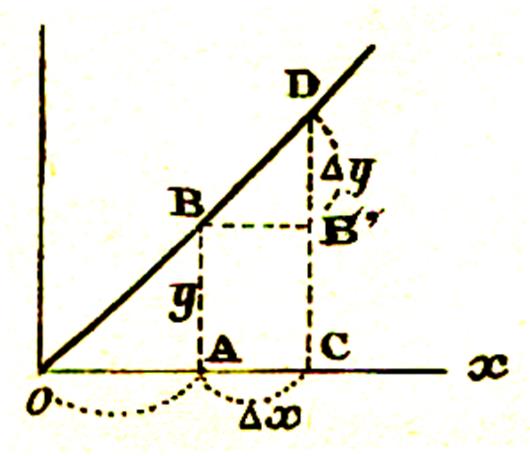
A un instant quelconque marqué par OA =
x , le trajet déjà parcouru AB = y A
l’instant OA + AC = x + Dx , le
trajet parcouru devient CD
= CB’ + B’D = y + Dy Sur la figure : DB’ est Dy et BB’ est Dx et dire que :
C’est à dire que l’angle DBB’ ( caractérisé par |
|
Cas où la règle
de trois ne s’applique pas .
Ce sont les cas où la fonction n’est pas
représentée par une équation du 1er degré , n’est pas figuré par une droite , mais est
représenté par une courbe dont la pente n’est pas constante .
La « vitesse d’accroissement » de la
fonction est donc variable . Et par suite , il est intéressant de
connaître les diverses valeurs que prend
cette vitesse .
1er Exemple :
Pour un corps tombant en chute libre , l’espace
parcouru « y » ( en mètre) est au bout du temps « x » ( en
secondes)
Relation équation 1 y = 5 x2
|
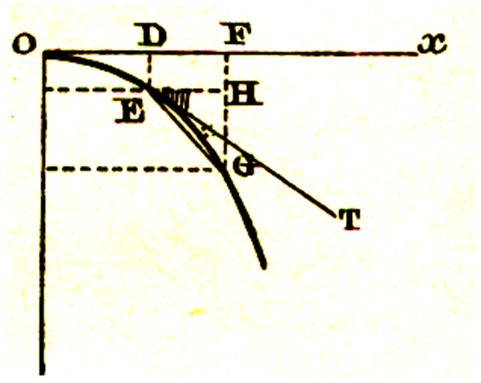
Pour le
temps OD = x , le trajet
est DE = y Pour un temps légèrement accru et devenu OF = OD
+ DF = x +Dx , le trajet devient FG soit
FH+HG, soit y + Dy et l’on a : Relation équation 2 : y + Dy = 5 (x +Dx)2 |
|
Nous avons un système : (1) et (2)
soit y = 5 x2 et y
+ Dy = 5 (x +Dx)2
Par soustraction membre à membre nous avons :
Dy = 5 (x + Dx)2 -
5 x2
d’où Dy = 5 (x2
+ 2xDx + Dx2 ) - 5 x2
Dy = 5 x2
+ 10xDx + 5Dx2 - 5 x2
Dy = 10xDx + 5Dx2
Dy = Dx (10x + 5Dx)
et enfin
= 10x + 5Dx
ce résultat
est la vitesse moyenne de chute entre le
temps « x » et le temps « x + Dx ».
Si l’on fait Dx = 0,1 sec. ; puis Dx = 0,01 ; puis Dx = 0,00….01 on a la vitesse moyenne successivement entre le
temps « x » et « x +
0,1 »
Ou « x + 0,01 » ou « x + 0,00……01 »
Evidemment , à la limite Dx
décroissant jusqu’à 0 , on a « la vitesse moyenne entre x et x »
décroissant jusqu’à 0 , on a « la vitesse moyenne entre x et x »
On peut donc écrire
Limite
(pour Dx = 0 ) = vitesse au temps x.
Or , cette
limite ( pour Dx = 0 ) se calcule par l’équation ( 3) en y faisant Dx =0
Limite
= 10 x
+ 0 = 10x
(4) Limite
= 10 x
Pour marquer ce passage à la limite , pour marquer
que Dx
a décru jusqu’à zéro , on change un peu , très peu , la notation. Dx accroissement petit de x est
remplacé par d x , signifiant «
accroissement infiniment petit de x , et
Dy accroissement petit de « y »
est remplacé par d y , accroissement infiniment petit de « y ».
Donc
l’équation (4) s’écrit 
=
10x
Ainsi pour la chute libre d’un corps , on a le
tableau suivant :
De la loi des espaces , y = x2 ,
nous avons déduit la loi des vitesses : v = =
10x
|
Temps « x » |
0 |
1 |
2 |
… |
x |
|
Vitesse : |
0 |
10 |
20 |
|
10x |
Nous avions « y » l’espace , fonction
de « x » , nous avons maintenant en outre la vitesse
v = =
10x
Une nouvelle fonction de « x » , déduite
de la première fonction , ou comme on
dit « dérivée » de la
première fonction qui elle , est dite alors « fonction primitive »
y = 5 x2 est ici la fonction primitive
v = = 10x est ici la fonction dérivée
La
dérivée d’une fonction est « sa vitesse d’accroissement » quand la
variable est le temps.
Autre exemple : Dérivée d’une fonction quand la variable
est une longueur.
|
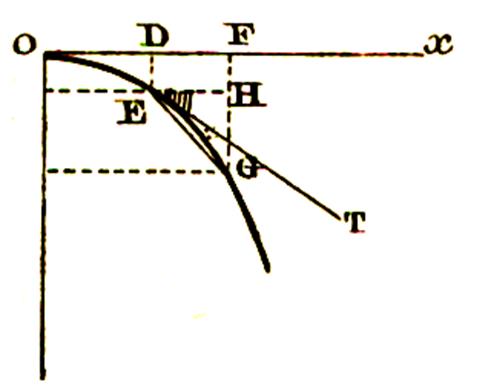
Soit la courbe ainsi construite . A tout abscisse
OD =x correspond une ordonnée DE = y = x2 (1) Pour un
accroissement petit Dx = DF , l’ordonnée
devient : FG= y +Dy = (x + Dx)2
= x2 + 2xDx + Dx2
(2) Par soustraction , les équations (1) et (2)
donnent : Dy = 2xDx + Dx2 |
|
D’où
= = 2x
+ Dx
Géométriquement , caractérise l’angle HEG , donne la pente de la
corde EH.
Lorsque Dx décroît
jusqu’à 0 ( et s’écrit alors d x
, Dy décroît
jusqu ‘ à 0 ( et s’écrit alors d y , l’équation (3) devient = 2x
En même temps la corde EH est devenue la tangente
ET et le
rapport limite du rapport donne la pente de la tangente ET.
Ainsi y = x2 est ici la fonction primitive , = 2x est ici la fonction dérivée , c’est en
quelque sorte la vitesse d’accroissement de la fonction : elle est
représentée par la pente sur l’horizontale de la tangente de la courbe .
Intérêt que
représente l’étude de la dérivée :
Cet intérêt est visible pour les physiciens , dans
le cas de la chute d’un objet (vu précédemment) .On étudie assez facilement par
expérience la loi des espaces
parcourus en chute libre , car on
n’a qu’à déterminer les positions du corps qui tombe de 1 ; 2 ;
3 ;…. Secondes .Après cela , on peut bien étudier la loi des vitesses , il
faudrait encore plus de patience ,
encore plus d’habileté que pour la loi des espaces . Mais , grâce au calcul que nous offrent , les mathématiques , cette deuxième partie
des recherches expérimentales est
superflue ; elle peut – être supprimée .
La loi y = 5 x2 suffit pour conclure v = =
10x
Ainsi le calcul de la dérivée rend service au
physicien . Il rend service au mathématicien en lui donnant des
renseignements précieux sur l’allure
d’une courbe et joue un grand rôle dans la discussion des problèmes .
Soit par exemple à étudier la courbe ci
–dessous :
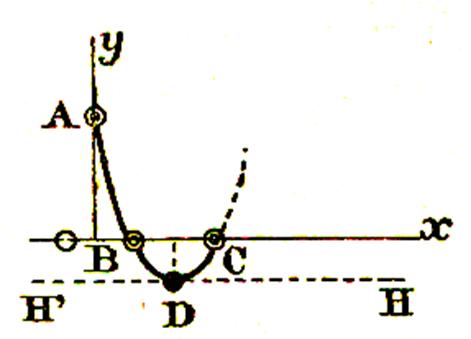
(pré requis : 1°) calculer y = x2 – 4 x + 3 pour « x = 0 » ; 2°) résoudre
l’équation du second degré 0 = x2 – 4 x + 3 )
|
y = x2 – 4 x + 3 On
voit d’abord que : pour x =
0 on a y = 3 La courbe passe par le point A . Pour y = 0 on a
0 = x2 – 4 x + 3 ( x
= 2 ± 1) , d’où x’ = +1 ; x’’ = + 3 la courbe passe
par B( +1) et C ( +3) |
|
Voilà ce qui
se trouve par les « moyens ordinaires » : les trois points
blancs de la figure ( A ; B ;C
)
Et voici ce que l’on trouve avec la dérivée :
Cette dérivée est
= 2x – 4
.
(résoudre : 2x – 4 = 0) Elle s’annule pour x = 2 et on a alors
y = x2 – 4 x + 3 ; y = 22 – 4 
2
+ 3 =
-1
Donc la courbe passe par le point
« D » ( point noir sur la
figure) de coordonnées 2 et –1 . et de plus , la
dérivée est nulle , c’est à dire ( voir dérivée d’une
fonction quand la variable est une longueur)que la pente sur l’horizontale de la tangente à la courbe est nulle ; c’est à dire que
la tangente à la courbe en D est
horizontale .
On voit combien
la connaissance de ce point D de cette tangente H’H favorise le tracé , et plus généralement
comment elle favorise la recherche du maximum ou du minimum . (voir la figure
précédente)
Remarque :
la fonction « y » était ici du second degré , la dérivée n’est
que du 1er degré ; c’est ce qui facilite la discussion .
RECHERCHE
DES DERIVEES.
Les dérivées étant importantes à connaître , il
faut essayer de les calculer , au moins dans les cas principaux . Et d’abord
pour les expression algébriques entières
.
1°) Nous avons vu que la fonction
du premier degré
y = a x
donne la dérivée = a
(si y = 4
x ; = 4 )
2°) Nous
avons vu la fonction du second degré
que la fonction
y = x2 donne la
dérivée = 2x
que la fonction
y = 5x2 donne la
dérivée = 10x
.
Il est facile de comprendre et on trouvera
aisément que :
que la fonction
y = a x2 donne la
dérivée = ax
3°) On trouvera de même que :
y = a x3 donne la dérivée = 3 ax2
y = axn donne la dérivée = na
xn-1
Ainsi , pour les expression algébriques entières , on sait passer de la fonction
primitive a xn
à la dérivée
na
xn-1 et inversement de la
fonction dérivée na
xn-1 à la fonction primitive
a xn
.
DERIVEE SECONDE .
Dans le cas d’un mouvement uniforme , le chemin
parcouru « y » , en fonction
du temps « x » , est y = ax . La vitesse
dans ce mouvement , est la dérivée :
v
= = a
Elle est constante . Il n’y a plus rien à ajouter.
Dans le cas de la chute libre d’un corps , le mouvement est uniformément
accéléré , le chemin parcouru ( y ) est
y = 5 x2 . La vitesse dans ce mouvement , est la dérivée , elle est v = = 10x
Elle n’est pas constante . Elle croît
avec « x » ; elle
est fonction de « x ». Elles croît avec une certaine vitesse . On l’appelle « la
vitesse de cette vitesse » que l’on note
dv sur la d x; et la 
est la dérivée de cette dérivée . Cette
dérivée on l’appelle la dérivée seconde
de la primitive . Ici , elle est
= 
=
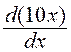10 (*)
* Nous avons
arrondi les nombres . En réalité elle est de 9,81 ; car en réalité la loi des espaces est y = 
9,81
x2 = 4,905 x2 et non de 5x2
Elle est constante , il n’y a plus rien à ajouter .
En physique , en mécanique , on l’appelle «
l’ accélération »
CONVENTION D’ECRITURE :
On a v
= donc
peut s’écrire
et on convient de l’écriture 
signifiant par là
que c’est la dérivée seconde de y
DERIVEE TROISIEME :
Imaginons un mouvement régi par la loi y = a x3
Sa dérivée est
= 3ax2 . Cette dérivée est une
fonction de « x » qui croît avec « x » ; et qui croît
avec une vitesse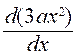 
qui est la dérivée de 3ax2 , qui
est donc 2 ( 3ax) . C’est la dérivée de
la dérivée ; c’est la dérivée seconde . Donc = 23ax
= 6ax
Cette dérivée- seconde est une fonction de
« x » qui croît avec « x » et qui croît avec une vitesse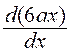 
= 6a
C’est la
dérivée de la dérivée seconde , c’est la dérivée troisième 
Donc = 6a
Ici elle est constante . Il n’y a rien à ajouter.
On voit que si on part d’une expression de degré
élevé y = axn
, on aura des dérivations successives en nombre élevé ( « n »
dérivation ; puisque chaque dérivation abaisse de « 1 » le degré
de l’expression ).
On peut représenter la fonction primitive par f(x) et écrire
y = f(x) , ce qui se lit et se comprend : « y est une certaine
fonction de « x » ». ( voir « fonction généralités » pour en savoir
plus )
4.
DERIVEES SUCCESSIVES.
La dérivée d’une fonction « y= f
(x) » est en général une fonction
de « x » , « y’= f’(x) »
qui peut elle-même admettre une dérivée ; cette dérivée de la
dérivée s’appelle dérivée seconde de « x » , et on la désigne
par « y’’ = f’’(x) »
Les dérivées successives s’écrivent 
; 
; 
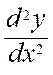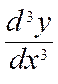ou bien
y’ ; y’’ ; y’’’ ;… ou bien encore f’’(x) ;
f’’’(x) ; f’’’’(x) ;…….
Ecritures équivalentes :
|
Désignation |
Notation 1 |
Notation 2 |
Notations 3 |
|
Dérivé première se note : |
|
y’ |
f’’(x) |
|
Dérivée seconde , se
note : |
|
y’’ |
f’’’(x) |
|
Dérivée « troisième », se note : |
|
y’’’ |
f’’’’(x) |
|
|
Exemples : |
|
||||
|
|
|
« y
= x 3 - 5 x² + 8 x – 11 » |
|
|
||
|
|
« y
‘ =
3 x 2 - 10 x +
8 » |
|
||||
|
|
« y
‘’ =
6 x - 10 » |
|
||||
|
|
On peut ainsi , dans certain cas , calculer les
dérivées successives d’une fonction. |
|
||||
|
|
|
|
||||
|
|
Application :
Formule du binôme. |
|
||||
|
|
« n »
étant un entier positif , ( h + x ) n est un polynôme homogène de degré
« n » en « h » et
« x » , et , on peut écrire : |
|
||||
|
|
(1) ( h + x ) n = h
n + C1 h n-1
x + C2 h n-2 x²
+ …..+ Cn xn ………….. ; ( C
n = 1 ) |
|
||||
|
|
|
|
||||
|
|
Prenons
les dérivées des deux membres ; elles
sont évidemment identiques. |
|
||||
|
|
«
n ( x + h ) n-1 |
C1 h
n-1 + 2 C2 h n-2 x + 3 C3 h n-3 x²
+ …….. |
|
|||
|
« n ( n-1 ) ( x + h) n-2 » |
2. 1 C2 h n-2 + 3
. 2 . C3 h n-3 x + …….. |
|||||
|
« n ( n-1 ) (
n – 2 ) ( x + h) n-3 » |
3 . 2 . 1 .
C3 h n-3 + …….. |
|||||
|
…………………………… |
…………………………… |
|||||
|
|
Faisons « x =
0 » , nous aurons : |
|
|
|||
|
|
« n = C1 » |
Ou « C1= |
|
|||
|
|
|
|
|
|||
|
|
« n ( n – 1) = 2 . 1 . C2 » |
C2 = |
|
|||
|
|
« n ( n – 1)( n – 2) = 3. 2 . 1 . C2 » |
C3 = |
|
|||
|
|
……………………………………………… |
……………………………………….. |
|
|||
|
|
Remarquer que C 2 = C1 |
|
|
|||
|
|
En permutant
« n » et « x » dans l’équation ( 1) , on a donc |
|
|
|||
|
|
( x + h ) n = x
n + |
|
||||
|
|
|
|
||||
|
|
Exemples : |
|
||||
|
|
|
|
||||
|
|
|
( x + 1 ) 4
= x 4 + 4 x 3 + 6
x² + 4 x + 1 |
|
|||
|
|
|
( x – 1 ) 7
= x 7 – 7
x 6 + 21 x 5 -
35 x 4 + 35 x 3 – 21 x² + 7 x – 1 |
|
|||
|
|
|
|
||||
|
|
|
|
|
|||
|
|
|
|
||||
|
|
|
|
||||
|
|
|
|
||||
Expression , au moyen de ses
dérivées , de la nouvelle valeur que prend une fonction « y » .
EXERCICE N°1 :
La fonction est du premier degré :
y = ax ou f(x) = ax
Donnons à « x » un accroissement
« h » quelconque ; grand ou petit .
La fonction prend un accroissement correspondant
« k »
y + k = a ( x + h ) = ax + ah
ou
f( x + h ) = ax + ah
(1)
or , ax, c’est l’ancienne
valeur de « y » ou « f(x) »
et « a » est la dérivée de la fonction
« y » ou « f(x) » ( y’ ou
f ’(x) )
donc la relation (1) s’écrit : f( x + h ) = f(x) + h f ’(x)
EXERCICE N°2 : la fonction est du second
degré :
. y
= a x 2 ou
f(x) = a x 2
pour
l’accroissement « h »
donné à « x » , y prend l’
accroissement « k »
(1) y +
k =
a ( x + h ) 2 = ax2 + 2 ax .h + a . h2
or , ax2
, c’est « y » ou
« f(x) «
2ax c’est la dérivée ou f ‘ (x)
« a » c’est la demi – dérivée de
2ax ; c’est la moitié de la dérivée seconde , c’est f ‘’
(x)
Donc , la relation (1) s’écrit
y + k = f ( x + h) :
(
Avec : ax2 = f(x) ; + 2
ax .h =
h . f ‘ (x) ; + a .
h2 = f ‘’
(x) .h2 )
f ( x + h ) = f(x) +
f’
(x) + 
f’’( x)
EXERCICE N°3 :
soit la fonction y = a x3 du 3e degré .
On trouvera de même que :
f ( x + h )
= f(x) + f’ (x) + f’’( x) +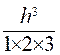
f ’’’( x)
Exercices : On fera de pareils exercices avec
des fonctions qui ne sont pas réduites à leur terme le plus élevé . Avec y = ax3 + b x2 + cx + d + …Etc. …
S’il s’agit d’une expression algébrique entière ,
on trouvera un développement analogue ; une série de termes célèbre , sous
le nom de série de Taylor . A chaque dérivation le degré s’abaisse de
« 1 » , donc on arrive au degré
0 à une expression constante , qui n’admet plus de dérivée.
La série , dans ce cas est limitée .
Mais il est des expressions qui donnent des
dérivées sans fin ! ! ! !et dont le développement en série
de Taylor , est par suite une série illimitée .
( Cette série illimitée est utilisable si elle est convergente)
On comprend donc combien cette étude est attachante
.
Donnons – en des exemples .
DERIVATION
INDEFINIE : EXPRESSIONS
ALGEBRIQUES à PUISSANCES
NEGATIVES.
Soit y = 
;
Qu’on peut écrire y = x-1
C’est une expression à puissance négative . Si elle
suit la règle « recherche des dérivées » ( est elle la suit en effet ) , la dérivation donne le degré
–2 ; puis –3 ; ..et ainsi de suite, évidemment , on n’arrive jamais
au degré zéro ; la dérivation se poursuit sans fin .
Voici , en effet , la première dérivation . On a
(1) y = et
(2) y + dy = 
par soustraction , on obtient : dy = -
= - 
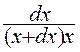
D’où = - 
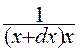
Mais le rapport a été calculé pour dx = 0
Donc : = - 
= - x –2
Remarque : on peut écrire cette dérivée en
appliquant la règle y = axn donne la dérivée = na
xn-1
En effet xn a pour dérivée
(n) x (n-1) de même x-1 a pour
dérivée (-1)x(-1-1) soit (-1)x(-2) ou -
Exercices : Continuer ces
dérivations successives. On trouve :
. f(x)
fonction primitive
. f ’ ( x) -
. f ’’ ( x) + 
. f ’’’ ( x) - 
Etc. ;……
DEVELOPPEMENT
DE 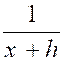en série
. ( d’ après
la formule de Taylor )
D’après la formule de Taylor , comme on a : f ( x + h) =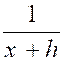
f (x) = ; f ’ ( x)
= - ;
etc. …..
On obtient :
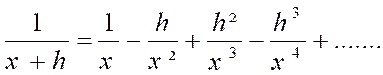
Fonction y
= sin. x ( Autre exemple de dérivation
indéfinie ):
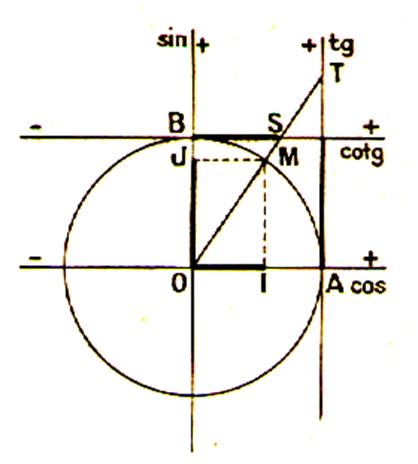
(pré requis : le cercle trigonométrique)
Il suffit d’avoir quelques notions de trigonométrie
pour prendre la dérivée de cette fonction
par le moyen indiqué.
|
y +
dy =
sin.(x + dx) Par soustraction , on obtient : dy = sin ( x + dx) – sin. x
= 2 sin d’où
|
|
Quand dx tend vers 0 , le rapport qui forme le 1er
facteur tend vers 1 ; le second
facteur tend vers Cos.x Donc = cos . x
La dérivée du sinus est le cosinus .
Calculons maintenant la dérivée du cosinus (
dérivée second du sinus )
On a : y =
cos x et y + dy
= cos ( x + dx)
Par soustraction
:
dy = cos ( x + dx ) – cos x
= - 2 sin 
sin( x + )
d’où
|
|
|
Et à la limite pour dx = 0
= - sin x
La dérivée du cosinus est le sinus pris en signe contraire .
On pourra remplacer ces calculs par le raisonnement
suivant :
|
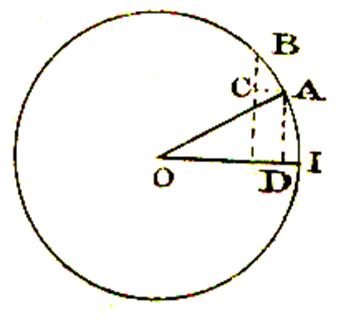
Sur la figure : BC = d (sin x) = dy AB = dx IA = arc
x Donc Or les triangles semblables ABC , OAD donnent
Donc |
|
La dérivée
de sin
x est donc cos.x . Au point de vue des signes , on voit que sin x
augmente avec « x » ; donc , la dérivée de sin x est + cos x